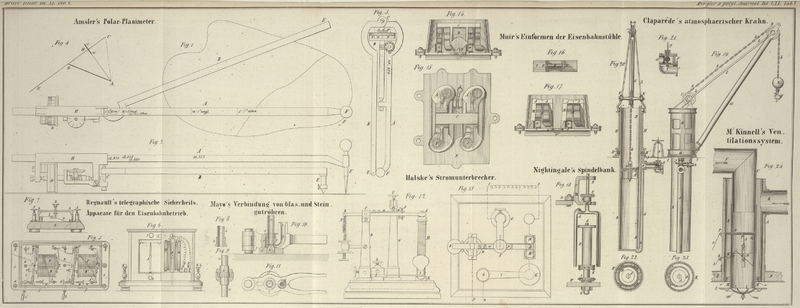
| Titel: | Ueber das Polar-Planimeter; von J. Amsler. |
| Fundstelle: | Band 140, Jahrgang 1856, Nr. LXXIII., S. 321 |
| Download: | XML |
LXXIII.
Ueber das Polar-Planimeter; von J. Amsler.
Mit Abbildungen auf Tab.
V.
Amsler, über das Polar-Planimeter.
Die zahlreichen Abhandlungen, welche in neuester Zeit über Planimeter von
verschiedenartiger Construction geschrieben wurden, zeigen daß allgemein das
Bedürfniß nach einem einfachen Instrumente dieser Art
gefühlt wird. Ein Planimeter herzustellen, welches genauere Resultate gibt, als ein
gut gearbeitetes Wetli'sches oder Hansen'sches Instrument, ist eine Aufgabe, die an und für sich
interessant, aber kaum von praktischem Belang ist.
Das von mir construirte Polar-Planimeter
Eine kurze Notiz darüber findet man Cosmos, T. VIII p. 212; eine ausführliche Besprechung und Vergleichung mit andern
Planimetern enthält die Vierteljahresschrift der
naturf. Gesellschaft in Zürich im ersten und zweiten Heft. Diese
Abhandlung erschien besonders abgedruckt bei Beck und Sohn in
Schaffhausen, unter dem Titel: „Ueber die mechanische Bestimmung
des Flächeninhaltes, der statischen Momente und der
Trägheitsmomente ebener Figuren, insbesondere über ein neues
Planimeter. Von J. Amsler.“
dürfte, nach vielfältigen Erfahrungen, den meisten praktischen Anforderungen
genügen, indem es ausreichend genau, äußerst einfach, bequem zu handhaben und
wohlfeil ist. Ich betrachte es daher als eine Art Pflicht, das Instrument in weitern
Kreisen bekannt zu machen und für die Anfertigung brauchbarer Exemplare zu
sorgen.
Von den verschiedenartigen Formen, in welchen ich hier das Planimeter ausführen ließ,
schienen vorzugsweise zwei sich zu empfehlen, welche in natürlicher Größe in Fig. 1, 2 und 3 auf Tab. V
dargestellt sind. Fig. 1 und 2 zeigen Grund- und
Aufriß des einen Instruments, Fig. 3 stellt das andere
im Grundriß dar.
Zum Gebrauche setzt man das Planimeter so auf das die Zeichnung enthaltende Papier,
wie Fig. 1
zeigt, daß nämlich die Rolle D, die Nadelspitze E und die Spitze des Fahrstiftes F aufsitzen, und drückt die Spitze E sanft
gegen das Papier. Sodann bringt man die Spitze F auf
einen bezeichneten Punkt des Umfangs der zu messenden Figur, und liest den Stand der
Rolle D ab. Nun verfolgt man den Umfang (von rechts nach
links herum) bis man auf den Ausgangspunkt zurückkommt, liest abermals den Stand der
Rolle ab und subtrahirt die zweite Ablesung von der ersten.
Befindet sich die Spitze E (der Pol) außerhalb der umfahrenen Figur, so gibt die gefundene
Differenz unmittelbar den gesuchten Inhalt an. Die Flächeneinheit, in welcher dieser
ausgedrückt ist, richtet sich nach der Stellung, welche der in der Hülse H mit mäßiger Reibung verschiebliche Stab A einnimmt. Die an seiner obern Fläche angebrachte
Theilung dient zur Einstellung für eine gewünschte Maaßeinheit.
Befindet sich dagegen die Spitze E
innerhalb der umfahrenen Fläche, so muß man vor der
Subtraction zur ersten Ablesung der Rolle D eine Zahl
addiren, welche auf einer Seitenfläche des Stabes A
zunächst neben dem Theilstrich gravirt ist, auf welchen man eingestellt hat.
Das in Fig. 3
dargestellte Instrument unterscheidet sich von dem vorigen nur dadurch, daß der Stab
A eine unveränderliche Länge hat, daß man also die
Flächeninhalte immer in derselben Einheit ausgedrückt erhält.
Die Dimensionen beider Instrumente sind so gewählt, daß sie bequem einem
mathematischen Bestecke beigefügt werden können.
Ein wesentlicher Punkt ist die Wohlfeilheit der
Instrumente. Ein Instrument von der in Fig. 1 und 2 dargestellten
Einrichtung kostet in Schaffhausen inclusive Etui
50–60 Frcs. (23 fl. 48 kr. bis 28 fl. 36 kr.); ein Instrument mit
unverstellbarem Fahrstift kostet 45–50 Fr. (21 fl. 30 kr. bis 23 fl. 48
kr.).In Frankreich, England, den Vereinigten Staaten und Bayern, wo das
Polarplanimeter patentirt ist, kann man es bei nachgenannten Mechanikern
beziehen: in Paris bei Lerebours und Secretan. Place du pont neuf 13; in London bei Gebrüdern Elliott, 56 Strand; in Philadelphia bei Amsler und Wirz, 211 Chestnut
street; in München bei T. Ertel und Sohn.
– In Zürich verfertigt es J. Goldschmid.
Eine einläßliche Untersuchung eines in gutem Stande befindlichen
Polar-Planimeters von einem competenten Fachmann hat bis jetzt, meines
Wissens, noch nicht stattgefunden, steht aber in Aussicht. – Dagegen erhielt ich über mehrere
in Gebrauch befindliche Instrumente Nachricht, die sich sämmtlich in der Anwendung
beim Eisenbahnbau, bei Katastervermessungen und beim Maschinenbau bewährten.
– Mit meinen eigenen zahlreichen Erfahrungen (ich habe bis jetzt selbst etwa
hundert solcher Planimeter repassirt und adjustirt) halte ich zurück, bis sich eine
unparteiische Stimme über den Gegenstand hat vernehmen lassen.
Um den „bescheidenen Zweifeln“ des Hrn. Professor Decher und Anderer, die sich für die
Sache interessiren, zu begegnen, bin ich bereit, jedem Fachmann der sich deßhalb
direct an mich wendet und mich gegen Schaden und Auslagen sicher stellt, ein
Polar-Planimeter für kurze Zeit auf Probe
zuzusenden. Dadurch dürfte eine weitläufige Besprechung der von genanntem Herrn in
der citirten Abhandlung gemachten kritischen Bemerkungen überflüssig werden;
indessen möchten die nachfolgenden Zeilen denjenigen Lesern nicht unangenehm seyn,
welche sich eine richtige theoretische Ansicht über den
Gegenstand bilden wollen.
Die im „Cosmos“ angedeutete und von
Hrn. Prof. Decher in diesem
Journal mitgetheilte Theorie des Polar-PlanimetersPolytechn. Journal Bd. CXL. S. 39
(erstes Aprilheft 1856). ist ohne Zweifel die einfachste, welche sich davon geben läßt; für den mit
den Principien des Infinitesimalcalculs Vertrauten ist sie vollkommen streng; sie
ist aber auch für denjenigen verständlich, welcher nur die Elemente der Mathematik
kennt.Die auf S. 33, Zeile 15 von unten, in der Decher'schen Abhandlung angeführte Stelle ist allerdings nicht klar
genug; sie könnte etwa so heißen: ...daß die über einander liegenden Theile der Flächenelemente abwechselnd
positiv und negativ sind...“. Dagegen ist der von Hrn. Professor Decher als „strenger und
bündiger“ ausgegebene analytische Beweis unrichtig, wie gezeigt
werden soll.
Auf Seite 36 seiner Abhandlung wird durch Δω die Aenderung des Coordinatenwinkels XCA (Taf. I, Fig. 6) bezeichnet.
Weiterhin folgt die Gleichung
ρΔφ'=hΔω.
Allein hierin bezeichnet Δω offenbar die Aenderung des Winkels XCD, sollte also durch ein anderes Zeichen, z.B.
durch Δω' ersetzt werden. Allerdings wird
dieser Gleichung die Bemerkung vorausgeschickt, daß für ein constantes
r und h die Aenderungen der
Winkel XCA und XCD einander gleich seyen. Allein in der nachfolgenden Gleichung
dφ/dω = r²/(2aρ)
– (a² + b² + 2ac)/(2aρ)
welche aus der obigen abgeleitet ist, wird r nicht als constant angesehen. Daß aber mit r zugleich sich auch der Winkel ACD, also auch der Winkel XCD ändert, wenn auch XCA constant bleibt, ist klar. Für veränderliches r sind also Δω und Δω' verschieden, und daher auch die
Differentialen dω und dω'. Vorstehende Gleichung muß also richtig so heißen
dφ/dω' = r²/(2aρ)
– (a² + b² + 2ac)/(2aρ)
und auf Seite 37 muß durchweg dω' statt dω geschrieben werden.
Nun läßt sich freilich leicht beweisen, daß die beiden daselbst für φ₁ – φ₀ gegebenen Ausdrücke ihre Werthe nicht ändern, wenn dω mit dω'
vertauscht wird, vorausgesetzt daß die Gerade AB
am Anfang und Ende der Bewegung genau die gleiche Lage einnimmt, und außerdem
bezüglich auf die Gerade BC nicht eine ganze
Umdrehung ausgeführt hat (eine Bedingung, die bei der für das
Polar-Planimeter gewählten Einrichtung immer erfüllt ist). Dagegen sind die
Ausdrücke für Δ₁φ und Δ₂φ durchaus unrichtig, außer in dem singulären
Fall, wo die den Werthen ω₀ und ω₁ entsprechenden Werthe von r (die vom Pol aus an dem Umfang der Figur gezogenen
Tangenten) einander gleich sind.
Ich erlaube mir, bei dieser Gelegenheit Hrn. Prof. Decher darauf aufmerksam zu machen, daß er genau
das nämliche Versehen bei der theoretischen Entwicklung der von ihm erfundenen
beiden Planimeter begangen hatPolytechn. Journal Bd. CXXXVI S. 168
und in diesem Bande (CXL) S. 40., indem er beidemal das Differential des dem Fahrstrahl r entsprechenden Polarwinkels mit dem Differential eines
Winkels verwechselt, der sich nach einem ganz andern Gesetze ändert. Dagegen sind
seine Endresultate richtig, weil sich die Unterschiede fortheben, wenn die
Integration über den Umfang einer geschlossenen Figur
ausgedehnt wird.
Was die praktische Würdigung des Polar-Planimeters durch Hrn. Prof. Decher anbetrifft, so liegt
derselben eine etwas seltsame, unklare geometrische Vorstellung vom Spiele des
Laufrädchens zu Grunde; sonst würde er erkannt haben, daß dieses bei meinem
Instrumente durchaus den nämlichen Bedingungen unterworfen ist, wie beim Wetli'schen, Bouniakovsky'schen, Decher'schen Planimeter. Bei
allen beschreibt der Punkt, in welchem das Laufrädchen seine (feste oder bewegliche)
Unterlage berührt, auf derselben eine gewisse Curve, während das Rädchen eine theils rollende, theils
gleitende Bewegung ausführt, theils sich um eine verticale Achse dreht (nämlich
relativ gegen die Unterlage). Bekanntlich kann aber jede nach einem willkürlichen Gesetze in einer Ebene erfolgende Bewegung
einer Geraden auf unendlich viele Arten auf eine fortschreitende und eine drehende
oder auf zwei drehende Bewegungen zurückgeführt werden, und zwar kann einer der
Drehpunkte fest angenommen werden, oder beliebig veränderlich seyn. Die Natur jener
Bewegung hängt aber offenbar durchaus nicht davon ab, in welcher Art man sie auf
andere Bewegungen zurückführt, sey es bloß in der Vorstellung oder durch die Art und
Weise wie man sie wirklich hervorbringt. – Ob also Drehungen, oder
Parallelverschiebungen und Drehungen, oder irgend andere zusammengesetzte
BewegungenDas Planimeter von Gierer in Fürth z.B. beruht auf
der Anwendung einer Leitcurve. benutzt werden, um ein Planimeterrädchen nach einem bestimmten Gesetz zu
führen, ist an und für sich durchaus gleichgültig. Von praktischer Wichtigkeit aber
ist es, die Gliederung des Apparates möglichst einfach zu machen. Beim
Polar-Planimeter ist die Führung des Laufrädchens auf zwei einfache Drehungen
zurückgeführt, oder wenn man den vom Punkte B (Taf. I,
Fig. 7)
durchlaufenen Kreisbogen durch eine Gerade ersetzt, auf eine einfache Drehung und
eine Parallelverschiebung; woraus sofort hervorgeht, daß das Instrument die
einfachste Gestalt besitzt, welche unter Anwendung eines Laufrädchens überhaupt
denkbar ist. – Zugleich wird man hieraus erkennen, daß die in Decher's Abhandlung (in diesem Bande
des polytechn. Journals auf S. 39) angestellten Betrachtungen, welche sich auf eine
übel angebrachte abstracte Vorstellung stützen, keinen realen Inhalt haben.
Was auf Seite 38 gesagt ist, weist gleichfalls keinen dem Polar-Planimeter
eigenthümlichen Nachtheil nach. Allerdings macht die Unsicherheit bei der gleitenden
Bewegung der Laufrolle dem Mechaniker Schwierigkeit (die sich freilich, wie ich
durch sehr zahlreiche Versuche gefunden habe, fast gänzlich beseitigen läßt). Allein
dieses trifft alle mit Laufrolle versehenen Planimeter
gleichmäßig. – Wie schon bemerkt, beschreibt bei allen der Berührungspunkt
des Laufrädchens eine gewisse Curve auf seiner Unterlage. So lange die Projection
der Rädchenachse mit der Bewegungsrichtung (mit der Tangente an jene Curve im
jeweiligen Berührungspunkt) einen rechten Winkel bildet, findet eine rein rollende
Bewegung statt; eine rein gleitende Bewegung dagegen, wenn dieser Winkel = 0 ist.
Jenes ist der für das Spiel des Apparates günstigste, dieses der ungünstigste Fall. Aber beide Fälle
treten in der Praxis nur ausnahmsweise und momentan ein; wiewohl sich für jedes Instrument der bezeichneten Gattung gewisse (praktisch aber ganz zu
umgehende und bedeutungslose) Curven auffinden lassen, bei deren Messung das
Laufrädchen beständig oder hauptsächlich unter den günstigsten oder ungünstigsten
Verhältnissen wirkt. Beschreibt z.B. beim zweiten Decher'schen Planimeter (Tab. I, Fig. 10) der Punkt A einen Kreisbogen, dessen Centrum der als fest
angenommene Punkt D, und dessen Radius = AD ist, so gleitet das Laufrädchen beständig. Schließt sich die von A durchlaufene Curve nur sehr nahe an einen solchen Bogen an, so tritt
genau der auf S. 38 bezeichnete Fall ein, welcher nach Hrn. Prof. Decher's Ansicht dem
Polar-Planimeter den Hals brechen soll. Es wäre sogar nicht schwer
nachzuweisen, daß die Uebelstände dieser Gattung für die praktisch wichtigen Fälle
am schwierigsten beim Bouniakovsky'schen und Decher'schen, am vollständigsten beim Wetli'schen Planimeter beseitigt werden können; das
Polar-Planimeter hält die Mitte ein.
Was die in der Praxis einzuhaltenden Fehlergränzen anbelangt (vergl. S. 39), so habe
ich meine Ansicht darüber in der oben citirten Abhandlung auseinander gesetzt,
worauf ich verweise. Es wäre mir aber lieb, eines Bessern belehrt zu werden, und
eine Reihe von Beispielen kennen zu lernen, wo bei Flächenberechnungen eine
Genauigkeit über 1/300 einen wirklich praktischen (nicht bloß illusorischen) Zweck
hat. – Ob aber dieser Grad von Genauigkeit gar so leicht mittelst eines
Schätzquadrates erreicht wird, als Hr. Prof. Decher zu glauben scheint, werden diejenigen
Leser zu beurtheilen wissen, welche mit diesem Instrumente zu arbeiten im Falle
waren.
Daß endlich Figuren, deren eine Dimension sehr klein ist, überhaupt mit keinem
Instrumente, und folglich auch mit keinem Planimeter genau berechnet werden können,
ist klar; im übrigen ist es, bei gehöriger Handhabung des Polar-Planimeters,
gleichgültig was für eine Gestalt die damit auszumessenden Flächen haben.
Schließlich sey mir noch die Bemerkung erlaubt, daß das Decher'sche Planimeter noch einer sehr wesentlichen Umformung fähig ist,
wodurch abermals zwei Lineale und zwei Drehungen wegfallen. In Fig. 4, Tab. V bezeichne
EC ein um den festen Pol C drehbares Lineal. Ein zweites, bei A mit dem Fahrstift versehenes Lineal AD sey damit durch die verticale Achse D verbunden. Längs des Lineals EC sey die dazu senkrechte Laufrolle aa so verschieblich, daß beständig < AHD = 90º ist. (Es kann dieses durch die
von Hrn. Prof. Decher
vorgeschlagene Einrichtung erreicht werden, aber auch durch einen von H nach der Mitte von AD
gehenden Stab, dessen
Enden um verticale Achsen drehbar sind; dadurch wird eine Schiebung durch eine
Drehung ersetzt). Macht man C
D = DA = a, das veränderliche CA = r, so ist offenbar
CA = r²/2a
Also in der von Hrn. Prof. Decher eingeführten Bezeichnung
Δφ/Δω = r²/2aρ
(wo aber Δω wie oben
bemerkt, nicht die Veränderung des Polarwinkels bezeichnet, welchen die Gerade AC bildet).
Statt verlängert durch den Punkt C zu gehen, braucht die
Achse der Rolle nur parallel zu DC zu seyn.
Schaffhausen, den 12. Mai 1856.
Tafeln