| Titel: | Neue merkwürdige Formel für den körperlichen Inhalt schief abgeschnittener Prismen, mit besonderer Rücksicht auf die wichtigen Anwendungen, welche sich von derselben zur Berechnung der aufzutragenden und abzutragenden Erdkörper bei Eisenbahnbauten, Wiesenanlagen und allen Nivellirungsarbeiten machen lassen; von Prof. Johann August Grunert zu Greifswald. |
| Fundstelle: | Band 149, Jahrgang 1858, Nr. I., S. 1 |
| Download: | XML |
I.
Neue merkwürdige Formel für den körperlichen
Inhalt schief abgeschnittener Prismen, mit besonderer Rücksicht auf die wichtigen
Anwendungen, welche sich von derselben zur Berechnung der aufzutragenden und
abzutragenden Erdkörper bei Eisenbahnbauten, Wiesenanlagen und allen
Nivellirungsarbeiten machen lassen; von Prof. Johann August Grunert zu
Greifswald.Vom Verfasser aus seinem „Archiv der Mathematik und Physik“,
1858, XXX. Theil, 4tes Heft, mitgetheilt.A. d. Red.
Mit Abbildungen auf Tab.
I.
Grunert, neue Formel für den körperlichen Inhalt.
I.
Man kennt die Formel, mittelst welcher der Inhalt eines schief abgeschnittenen
dreiseitigen senkrechten oder geraden Prismas bestimmt wird, und weiß auch, wie
wichtig diese Formel für die Berechnung der aufzutragenden und abzutragenden
Erdkörper bei Eisenbahnbauten, Wiesenanlagen und überhaupt allen
Nivellirungs-Arbeiten ist, indem es, insbesondere wenn diese Erdkörper von
unregelmäßiger Gestalt sind, wohl überhaupt keine andere Methode zu der, für die
Veranschlagung solcher Arbeiten so wichtigen Berechnung der auf- und
abzutragenden Erdkörper als die Anwendung der erwähnten Formel geben dürfte.
Bekanntlich erfordert die Anwendung dieser Formel die Kenntniß der drei Höhen des
Prismas und des Inhalts seiner horizontalen Grundfläche. Die Messung der drei
ersteren ist mit Hülfe der Nivellir-Latte und des Nivellir-Instruments
mit aller erforderlichen Genauigkeit leicht ausführbar und unterliegt nicht der
geringsten Schwierigkeit. Anders verhält es sich aber mit der Bestimmung des Inhalts
der horizontalen Grundfläche, welche die Messung der horizontalen Projektionen der
drei Seiten der oberen schiefen Grundfläche in Anspruch nimmt, und mit der
erforderlichen Genauigkeit nie ohne namhaften Zeitaufwand ausführbar, in der Praxis selbst zuweilen nicht von
allen Schwierigkeiten frei ist. Ueberdieß muß man aus diesen drei gemessenen
Projectionen den Inhalt der horizontalen Grundfläche nach der bekannten Formel für
den Inhalt des Dreiecks aus seinen drei Seiten berechnen, wozu die Ausziehung einer
Quadratwurzel erforderlich ist, die sich in diesem Falle nicht wohl anders, als nach
der gewöhnlichen elementaren Methode oder mittelst der Logarithmen ausführen läßt.
Um diese etwas weitläufige Rechnung zu umgehen, mißt man auch wohl nur die
horizontale Projection einer Seite der oberen schiefen Grundfläche und deren
horizontalen Abstand von der gegenüberstehenden Ecke dieser Grundfläche, wodurch man
sich eine Seite und die entsprechende Höhe der horizontalen Grundfläche verschafft,
woraus man dann deren Inhalt leicht berechnen kann; aber diese Messung genau
auszuführen, ist nicht ganz leicht und nimmt ziemliche Zeit in Anspruch.
Alle diese Schwierigkeiten werden vermieden, wenn man im Besitz einer Formel ist,
mittelst welcher man den Inhalt des Prismas aus seinen drei Höhen und den drei
Seiten der oberen schiefen Grundfläche berechnen kann, weil, wie schon gesagt, die
Messung der ersteren mittelst der Nivellir-Latte und des
Nivellir-Instruments mit großer Genauigkeit leicht ausführbar ist, und die
Messung der letzteren nur die unmittelbare Anlegung des Maaßstabes erfordert, wozu
ich noch bemerke, daß auch jede Höhe der oberen schiefen Grundfläche sehr leicht mit
dem Maaßstabe gemessen, und also der Inhalt dieser Grundfläche einfach aus
Grundlinie und Höhe berechnet werden kann. Eine allen diesen Erfordernissen
entsprechende Formel für den Inhalt schief abgeschnittener gerader dreiseitiger
Prismen will ich nun entwickeln, welche ich auch in theoretischer Rücksicht für sehr
merkwürdig und für eine Bereicherung der elementaren Stereometrie zu halten geneigt
bin, so daß es mir sehr wünschenswerth scheint, daß dieselbe künftig in den
stereometrischen Elementar-Unterricht und die betreffenden Lehrbücher
aufgenommen werde, namentlich auch deßhalb, weil dieselbe Gelegenheit zu so vielen
wichtigen praktischen Anwendungen darbietet.
II.
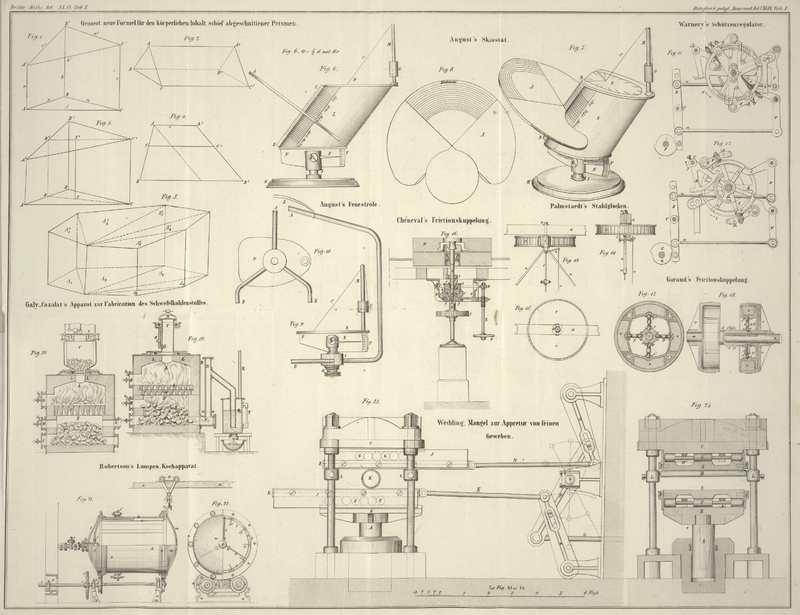
Auf Tab. I Fig.
1 sey ABC die untere Grundfläche des schief
abgeschnittenen geraden dreiseitigen Prismas ABCA'B'C',
auf welcher die drei Höhen AA', BB', CC' desselben
senkrecht stehen, und A'B'C' sey die obere schiefe
Grundfläche desselben. Der Kürze wegen bezeichne man die Inhalte der beiden
Grundflächen ABC und A'B'C'
respective durch Δ und Δ' und setze:
BC
= α,
CA
= β,
AB
= γ;
AA'
= a,
BB'
= b,
CC
= c;
B'C'
= a',
C'A'
= b',
A'B'
= c'.
Nach einer bekannten Formel der ebenen Geometrie ist
16 Δ² = 2 α² β² + 2 β² γ² + 2 γ² α² – α⁴ – β⁴ – γ⁴.
Offenbar ist aber
α² = a'² = (b – c)², β² = b'² – (c
– a)², γ² = c'² – (a – b)²;
folglich:
16 Δ² =
2{a'² – (b – c)²} {b'² – (c – a)²}
+ 2{b'²
– (c – a)²} {c'²
– (a – b)²}
+ 2{c'²
– (a – b)²} {a'²
– (b – c)²}
– {a'² – (b – c)²}² – {b'² – (c – a)²}²
– {c'² – (a – b)²}²,
woraus man nach gehöriger Entwickelung der einzelnen Theile
dieses Ausdrucks die folgende Formel erhält:
16 Δ² =
2a'²b'² + 2b'²c'²
+ 2c'²a'² – a'⁴ –
b'⁴ – c'⁴
– 2(a – b)² (a'² + b'² – c'²)
– 2(b – c)² (b'² + c'² – a'²)
– 2(c – a)² (c'² + a'² – b'²)
+ 2(a – b)² (b
– c)² + 2(b – c)² (c – a)² + 2(c – a)² (a – b)²– (a – b)⁴ – (b – c)⁴ – (c – a)⁴.
Nun überzeugt man sich leicht von der Richtigkeit der auch an sich merkwürdigen
allgemeinen algebraischen Relation:
1)
+ 2(a –
b)² (b
– c)² + 2(b – c)² (c – a)² + 2(c – a)² (a – b)² –
(a – b)⁴ – (b – c)⁴ – (c – a)⁴
= 0,
und es ist also nach dem Vorhergehenden:
16 Δ² =
2a'² b'² + 2b'²c'²
+ 2c'²a'² – a'⁴ –
b'⁴ – c'⁴
– 2(a – b)² (a'² + b'² – c'²)
– 2(b – c)² (b'² + c'² – a'²)
– 2(c – a)² (c'² + a'² – b'²)
oder, weil nach der schon oben angewandten Formel der ebenen
Geometrie
16 Δ'² = 2a'² b'² + 2b'²c'² + 2c'²a'²
– a'⁴ – b'⁴ – c'⁴
ist:
2) 16 Δ² =
16 Δ'² – 2(a – b)² (a'² + b'² – c'²)
– 2(b – c)² (b'² + c'² – a'²)
– 2(c – a)² (c'² + a'² – b'²)
oder
3) 16 Δ² =
16 Δ'² – 2a'²{ (a –
b)² – (b
– c)² + (c
– a)²}
– 2b'²{ (a – b)²
– (b – c)² + (c – a)²}
– 2c'²{– (a – b)²
– (b – c)² + (c – a)²}.
Leicht ergibt sich:
(a – b)² – (b
– c)² + (c
– a)² = – 2(a – b) (c
– a),
(a – b)² – (b
– c)² + (c
– a)² = – 2(b – c) (a
– b),
– (a – b)² – (b
– c)² + (c
– a)² = – 2(c – a) (b
– c);
und es ist also:
16 Δ² = 16 Δ'² + 4a'² (a – b) (c – a)
+ 4 b'² (b –
c) (a – b) + 4c'² (c – a) (b – c)
oder
Textabbildung Bd. 149, S. 4
oder auch:
Textabbildung Bd. 149, S. 4
und folglich:
4) Textabbildung Bd. 149, S. 4
Bezeichnen wir jetzt den Inhalt des schief abgeschnittenen dreiseitigen geraden
Prismas ABCA'B'C' durch P,
und denken uns durch A' eine mit ABC parallele Ebene gelegt, wodurch das schief abgeschnittene dreiseitige
gerade Prisma in ein gerades dreiseitiges Prisma und eine vierseitige Pyramide
zerfällt wird; so ist, wenn wir das von A oder A' auf die Ebene BCB'C'
gefällte Perpendikel durch h bezeichnen, offenbar:Wenn ABCA'B'C'
Fig.
2, ein beliebiges dreiseitiges Prisma ist, so kann man sich dasselbe,
indem man durch AA' eine mit BCB'C' parallele Ebene legt, zu einem
Parallelepipedon ergänzt denken, von welchem das dreiseitige Prisma die
Hälfte ist. Bezeichnet man nun die Entfernung der Kante AA' von der Seitenfläche BCB'C', d.h. ein von einem beliebigen Punkte in AA'
auf BCB'C' gefälltes Perpendikel durch H, so ist H .
der Inhalt des Parallelepipedons, folglichPrisma ABCA'B'C' = 1/2 H . ;und ist BCB'C' ein
Rechteck, so istPrisma ABCA'B'C' = 1/2 H . . .Dieser Satz ist oben bei der Bestimmung des Inhalts von P in Anwendung gebracht worden, und kann
überhaupt häufig bei Körperberechnungen mit großem Vortheil angewandt
werden, weßhalb man ihn in die Elemente aufnehmen sollte.
Textabbildung Bd. 149, S. 4
Textabbildung Bd. 149, S. 5
also:
5) Textabbildung Bd. 149, S. 5
Also ist nach 4):
6) Textabbildung Bd. 149, S. 5
und wenn man
7) 2s' = a' + b' + c'
setzt, so ist bekanntlich:
8) Textabbildung Bd. 149, S. 5
also:
9)Textabbildung Bd. 149, S. 5
oder:
10)Textabbildung Bd. 149, S. 5
Formeln, durch welche nun, wie verlangt wurde, P bloß durch a, b, c und a', b', c' ausgedrückt ist.
In der Praxis wird man sich am besten der Formel 6) bedienen, indem man den
Flächeninhalt Δ' der oberen schiefen Grundfläche
A'B'C'
durch Messung nur einer Seite und der dieser Seite entsprechenden Höhe des
Dreiecks A'B'C' bestimmt, was nie einer Schwierigkeit
unterliegt und immer mit der erforderlichen Genauigkeit durch unmittelbare Anlegung
des Maaßstabes ausführbar ist.Wenigstens die bis hierher entwickelten Formeln möchte ich zur künftigen
Aufnahme in den stereometrischen Elementar-Unterricht und die
betreffenden Lehrbücher sehr empfehlen.
III.
Wenn die Ebene A'B'C' nur wenig von der horizontalen Lage
abweicht, was bei praktischen Arbeiten häufig der Fall seyn wird, so sind die
absoluten Werthe der Differenzen a – b, b – c, c –
a nur klein, und es wird also auch der absolute
Werth der Größe
Textabbildung Bd. 149, S. 6
nur klein seyn. Setzen wir also
11) Textabbildung Bd. 149, S. 6
und folglich nach 6):
12) Textabbildung Bd. 149, S. 6
so kann in solchen Fällen zur Berechnung der in dieser Formel
vorkommenden Quadratwurzel vortheilhaft das Binomial-Theorem angewandt
werden, wodurch wir den folgenden Ausdruck erhalten:
13) Textabbildung Bd. 149, S. 6
oder
14) Textabbildung Bd. 149, S. 6
welcher eine desto leichtere Rechnung gewährt, je kleiner ε ist.
IV.
Nach einem bekannten Satze der Lehre von den Projectionen ist, wenn i' den Neigungswinkel der Ebene A'B'C' gegen den Horizont, d.h. im Allgemeinen gegen die Ebene ABC, bezeichnet:
Δ = Δ' cos i',
also nach 4) offenbar
15)Textabbildung Bd. 149, S. 7
folglich:
16)Textabbildung Bd. 149, S. 7
woraus:
17)Textabbildung Bd. 149, S. 7
oder
18)Textabbildung Bd. 149, S. 7
folgt, welche Formeln gleichfalls sehr bemerkenswerth und
mancher Anwendungen fähig sind.
V.
Wenn in Fig. 3
die Schwerpunkte der Dreiecke ABC und A'B'C' respective S und S' sind, so ist bekanntlich
AD = BD,
A'D' = B'D'; SD = 1/2 CS, S'D' = 1/2 C'S';
woraus zunächst auf der Stelle erhellet, daß die Linie SS', welche die Schwerpunkte der beiden Grundflächen des
Prismas mit einander verbindet, den Kanten AA', BB', CC'
des Prismas parallel ist, und daher auf ABC senkrecht
steht. Ferner ist nach einem leicht zu beweisenden Satze vom Trapezium:Wenn in Fig.
4 in dem Trapezium AA'BB' mit AA' und BB' die
Parallele CC' gebogen ist, so erhellet, wenn man
durch A eine Parallele mit A'B' legt, auf der Stelle, daßTextabbildung Bd. 149, S. 7oderCC' = AA' . BC/AB + BB' . AC/ABist.
DD' = 1/2 . AA' + 1/2 . BB',
SS' = 2/3 . DD' + 1/3 . CC';
folglich:
SS' = 1/2 . AA' + 1/3 . BB' + 1/3 CC'
oder
SS' = (AA' + BB' + CC')/3 = (a + b + c)/3.
Bezeichnen wir also die Entfernung der Schwerpunkte der Dreiecke ABC und A'B'C', nämlich der
beiden Grundflächen des schief abgeschnittenen geraden dreiseitigen Prismas, von
einander, oder nach dem Vorhergehenden die Entfernung des Schwerpunkts der oberen
Grundfläche von der unteren, durch E, so ist nach
5):
19) P = EΔ,
und nach 6) ist:
20)Textabbildung Bd. 149, S. 8
VI.
Ein schief abgeschnittenes gerades Prisma von beliebiger Seitenzahl kann man, wie
Fig. 5
zeigt, immer in mehrere schief abgeschnittene gerade dreiseitige Prismen zerlegen,
deren untere und obere Grundflächen wir mit Bezug auf die genannte Figur durch
Δ₁, Δ₁'; Δ₂, Δ₂'; Δ₃, Δ₃'; Δ₄, Δ₄'; Δ₅, Δ₅'
bezeichnen wollen. Bezeichnen wir dann ferner die Entfernungen
der Schwerpunkte der Grundflächen dieser schief abgeschnittenen geraden dreiseitigen
Prismen von einander, welche nach V. zugleich die
Entfernungen der Schwerpunkte der oberen Grundflächen von der unteren Grundfläche
des ganzen Prismas sind, respective durch
E₁, E₂, E₃, E₄, E₅
und den Inhalt des ganzen schief abgeschnittenen Prismas durch
P, so ist nach 19):
P = E₁Δ₁ + E₂Δ₂ + E₃Δ₃ +
E₄Δ₄ + E₅Δ₅.
Nach der Lehre vom Schwerpunkte ist aber, wenn wir die
Entfernung des Schwerpunktes der oberen Grundfläche des ganzen schief
abgeschnittenen Prismas von dessen unterer Grundfläche durch E bezeichnen:
E = (E₁Δ₁' + E₂Δ₂' + E₃Δ₃' +
E₄Δ₄' + E₅Δ₅')/(Δ₁' + Δ₂' + Δ₃' + Δ₄' + Δ₅'),
oder, wenn Δ' den Inhalt
der ganzen oberen schiefen Grundfläche unseres Prismas bezeichnet, so daß
Δ' = Δ₁' + Δ₂' + Δ₃' + Δ₄' + Δ₅'
ist:
EΔ' = E₁Δ₁' + E₂Δ₂' + E₃Δ₃' +
E₄Δ₄' + E₅Δ₅',
folglich auch, wenn i' den
Neigungswinkel der oberen Grundfläche gegen die untere bezeichnet:
EΔ' cos i'
= E₁Δ₁' cos i' + E₂Δ₂'
cos i' + E₃Δ₃' cos i' +
E₄Δ₄' cos i' + E₅Δ₅' cos i',
also nach dem schon oben angewandten bekannten Satze von den
Projectionen, wenn Δ den Inhalt der ganzen
unteren Grundfläche unseres Prismas bezeichnet:
EΔ = E₁Δ₁ + E₂Δ₂ + E₃Δ₃ +
E₄Δ₄ + E₅Δ₅.
Daher ist nach dem Obigen:
21) P = EΔ,
und die oben für das schief abgeschnittene gerade dreiseitige Prisma bewiesene Formel
19) gilt daher allgemein für jedes schief abgeschnittene gerade Prisma von
beliebiger Seitenzahl.
Aus der bekannten Construction, durch welche man den Schwerpunkt einer beliebigen
geradlinigen Figur, die man in Dreiecke zerlegt hat, nach und nach aus den
Schwerpunkten dieser Dreiecke zu finden pflegt, erhellet auf der Stelle, daß die
Entfernung E des Schwerpunkts der oberen Grundfläche
unseres Prismas von seiner unteren Grundfläche die gerade Linie ist, welche die
Schwerpunkte der beiden Grundflächen mit einander verbindet.
Wenn man in der oberen schiefen Grundfläche unseres Prismas drei ganz beliebige
Punkte A', B', C' annimmt, deren Entfernungen B'C', C'A', A'B' oder a', b',
c' von einander mißt und ihre senkrechten Abstände a, b, c von der unteren Grundfläche nach dem gewöhnlichen praktischen
Verfahren bestimmt, so ist nach 15):
Textabbildung Bd. 149, S. 9
wo wie früher
2s' = a'
+ b' + c'
ist, oder
Textabbildung Bd. 149, S. 9
also, wenn Δ und Δ' wie oben die ganze untere und obere
Grundfläche des schief abgeschnittenen mehrseitigen Prismas bezeichnen, da nach dem
schon mehrfach angewandten Satze von den Projectionen allgemein Δ = Δ' cos i' ist, nach 21):
22)Textabbildung Bd. 149, S. 10
oder
23)Textabbildung Bd. 149, S. 10
Bezeichnen wir den Inhalt des vorher auf der oberen Grundfläche unseres Prismas
beliebig angenommenen Dreiecks, dessen Seiten a', b', c'
sind, jetzt durch D'; so ist
D'² = s' (s' – a') (s' – b') (s' – c'),
also:
24)Textabbildung Bd. 149, S. 10
wo man D' auch durch Messung einer
Seite und der entsprechenden Höhe des betreffenden Dreiecks bestimmen kann.
Die vorstehenden Formeln, in denen alle zu messenden Elemente sich auf die obere
schiefe Grundfläche des Prismas beziehen, und in allen Fällen durch die bekannten
Methoden mittelst des Maaßstabes, der Nivellir-Latte und des
Nivellir-Instruments leicht und genau ermittelt werden können, gelten auch
für schief abgeschnittene gerade Cylinder, weil im Vorhergehenden natürlich die
Seitenzahl des Prismas sich beliebig groß annehmen läßt, die Seitenflächen desselben
beliebig klein angenommen werden können.
VII.
Wir wollen uns jetzt ein Prisma von beliebiger Seitenzahl von zwei gegen seine
parallelen Seitenkanten willkürlich geneigten Ebenen durchschnitten denken, wodurch
zwei Schnitte entstehen, deren Flächenräume wir durch Δ' und Δ₁', und den
Inhalt des zwischen diesen Schnitten enthaltenen Körpers durch P bezeichnen wollen. Die Schnitte Δ' und Δ₁' mögen der
Kürze wegen die Grundflächen dieses Körpers genannt werden. Denken wir uns nun ferner einen
auf den parallelen Seitenkanten des Körpers P senkrecht
stehenden Schnitt Δ, welcher entweder ganz
außerhalb oder ganz innerhalb des Körpers P liegt, so
daß im ersten Falle die Grundfläche Δ' zwischen
der Grundfläche Δ₁' und dem senkrechten
Schnitte Δ liegt, und bezeichnen die Entfernungen
der Schwerpunkte der Grundflächen Δ' und Δ₁' von dem senkrechten Schnitte Δ respective durch E
und E₁; so ist nach 21) offenbar
P = EΔ ∓ E₁Δ = (E ∓ E₁) Δ,
indem man in dem ersten der beiden obigen Fälle das obere, in
dem zweiten dieser beiden Fälle dagegen das untere Zeichen zu nehmen hat. Aus VI.
erhellet unmittelbar, daß die Schwerpunkte von Δ', Δ₁', Δ in einer und derselben auf dem Schnitte Δ senkrecht stehenden geraden Linie liegen, so
daß also E ∓ E₁ die Entfernung der Schwerpunkte der beiden Grundflächen des Körpers
P von einander, und folglich, wenn wir diese
Entfernung durch E bezeichnen, nach dem Obigen
25) P = EΔ
ist.
Nehmen wir nun etwa in der Grundfläche Δ' die
unter dem Winkel ί gegen Δ geneigt seyn mag, drei beliebige Punkte A', B', C' an, und messen deren Entfernungen B'C' = a', C'A' = b',
A'B' = c' von einander, so wie ihre senkrechten
Abstände a, b, c von der Ebene des senkrechten Schnitts
Δ; so ist, wenn D' den Flächeninhalt des Dreiecks A'B'C'
bezeichnet, bekanntlich:
Textabbildung Bd. 149, S. 11
also offenbar:
26)Textabbildung Bd. 149, S. 11
Ist das Prisma ein dreiseitiges, und sind a, b, c und a₁, b₁, c₁ die senkrechten Abstände der Ecken der
Grundflächen Δ' und Δ₁' von dem senkrechten Schnitte Δ, so ist bekanntlich
E = (a + b + c)/3, E₁
= (a₁ + b₁ +
c₁)/3;
also
Textabbildung Bd. 149, S. 11
oder, wenn wir die Entfernungen der Ecken der beiden
Grundflächen Δ' und Δ₁' von einander durch a, b, c
bezeichnen:
E ∓ E₁ = (a + b +c)/3,
also nach dem Obigen:
27) P = (a + b + c)/3 Δ.
Bezeichnen aber wie gewöhnlich a', b', c' die Seiten der
Grundfläche Δ' in der oben immer festgehaltenen
Ordnung, so daß nämlich, wenn wir diese Grundfläche durch A'B'C' bezeichnen, wie oben a' = B'C', b' = C'A', c' = A'B' ist, so ist:
28)Textabbildung Bd. 149, S. 12
Alle diese Formeln sind so entwickelt und dargestellt worden, daß die Bestimmung der
Größen, von denen sie abhängen, in der Praxis keiner Schwierigkeit unterliegt, was
mit ein Hauptzweck war, den dieser Aufsatz zu erreichen suchte.
Tafeln