| Titel: | Experimentelle Untersuchungen um die Dichtigkeit des Wasserdampfes für jede Temperatur zu bestimmen; von William Fairbairn und Thomas Tate. |
| Fundstelle: | Band 155, Jahrgang 1860, Nr. I., S. 1 |
| Download: | XML |
I.
Experimentelle Untersuchungen um die Dichtigkeit
des Wasserdampfes für jede Temperatur zu bestimmen; von William Fairbairn und Thomas Tate.
Vorgetragen vor der British Association for the Advancement of Science,
1859. – Aus dem Civil
Engineer and Architect's Journal, November 1859, S.
365.
Mit Abbildungen auf Tab.
I.
Fairbairn's experimentelle Untersuchungen um die Dichtigkeit des
Wasserdampfes für jede Temperatur zu bestimmen.
Ich beabsichtige im Folgenden die Skizze von einem Apparate und die Resultate der
Versuche mitzutheilen, wodurch ich in Verbindung mit Hrn. Thomas Tate das Gesetz der Dichtigkeit des Wasserdampfes und
anderer verdichtbarer Dämpfe direct auf experimentellem Wege zu ermitteln bezweckte,
so daß die bisherigen Hypothesen bezüglich der Relation zwischen dem specifischen
Volumen und der Temperatur des Wasserdampfes und anderer Dämpfe entweder bestätigt
oder berichtigt werden mußten. Unsere Versuche wurden nach einem ganz neuen Princip
durchgeführt, welches für jede Temperatur und jeden Druck, den Glasgefäße
auszuhalten vermögen, anwendbar ist.
Hinsichtlich der permanenten Gase ist das Gesetz für die Relation zwischen Temperatur
und Volumen als Gay-Lussac'sches oder Dalton'sches bekannt und wird
ausgedrückt durch die Gleichung:
(V × P)/(V₁
× P₁) = (458 +
t₁)/(458 + t) (1).
Die Dichtigkeit des Wasserdampfes wurde mit Genauigkeit durch directen Versuch bei
der Temperatur von 212° F. – und nur bei dieser Temperatur –
mittelst der Methode von Dumas bestimmt. Bei 212°
F. ist seine Dichtigkeit eine solche, daß sein Volumen 1670mal so groß ist, als
dasjenige des Wassers welches ihn erzeugte. Substituirt man diese Werthe von
Volumen, Temperatur und Druck, so erhält man für das Dampfvolumen, welches eine
Wassereinheit bei irgend einer andern Temperatur liefert,
V – (1670 × 15)/670
× (458 + t)/P
oder
V = 37⅓ (458 + t)/P (2).
Dieses ist die bekannte Formel, auf welcher bis jetzt unsere Tabellen für die
Dichtigkeit des Wasserdampfes fußten, nach denen wir die Leistung der Dampfmaschinen
zu berechnen pflegen.
Theoretische Betrachtungen machen jedoch die Anwendbarkeit der obigen Formel auf den
Wasserdampf und andere verdichtbare Dämpfe sehr zweifelhaft. Vor einigen Jahren
kamen Dr. Joule und Professor
William Thomson bei Anwendung der neuen dynamischen
Wärmetheorie auf das Carnot'sche Gesetz zu dem Resultat,
daß für Temperaturen über 312° F. hinsichtlich des Wasserdampfes eine
bedeutende Abweichung von dem für die permanenten Gase geltenden Gesetze
stattfindet. Später, im Jahre 1855, stellte Prof. Macquorn Rankine eine neue theoretische Formel für die Dichtigkeit des
Wasserdampfes, unabhängig vom Gay-Lussac'schen Gesetze auf, welche die Vermuthung Thomson's bestätigt. Die Richtigkeit dieser Hypothesen
muß jedoch noch durch directe Versuche nachgewiesen werden.
Die Dichtigkeit des Dampfes wird dadurch bestimmt, daß man ein bekanntes Gewicht
Wasser in einer Glaskugel von bekanntem Inhalt verdampft und die Temperatur, bei
welcher alles Wasser in Dampf verwandelt wird, genau beobachtet. Aus diesen drei
Elementen, Volumen, Gewicht und Temperatur, ergibt sich das spec. Gewicht. Aber bei
Anwendung dieser Methode müssen folgende zwei Schwierigkeiten überwunden werden:
erstens ist man wegen des Dampfdruckes genöthigt die Glaskugel in einem starken und
folglich undurchsichtigen Gefäße zu erhitzen; zweitens würde es, da mit einer
Erhöhung der Temperatur über die Sättigungs-Temperatur der Dampf schnell an
Volumen zunimmt, jedenfalls unmöglich seyn, durch das Auge die Temperatur zu
bestimmen, bei welcher sämmtliches Wasser verdampft ist. Die
Sättigungs-Temperatur, d.h. die Temperatur bei welcher sämmtliches Wasser in
Dampf verwandelt worden ist, ohne daß ein Theil des Dampfes überhitzt wurde, muß
aber mit der größten Genauigkeit bestimmt werden, sonst sind die Resultate
werthlos.
Um diese Schwierigkeiten zu beseitigen, war ein genaues und empfindliches Verfahren
zur Bestimmung des Sättigungspunktes erforderlich; diesem Zweck entspricht unser
Sättigungsmesser (saturation gauge), in dessen Anwendung
das Neue der gegenwärtigen Versuche besteht.
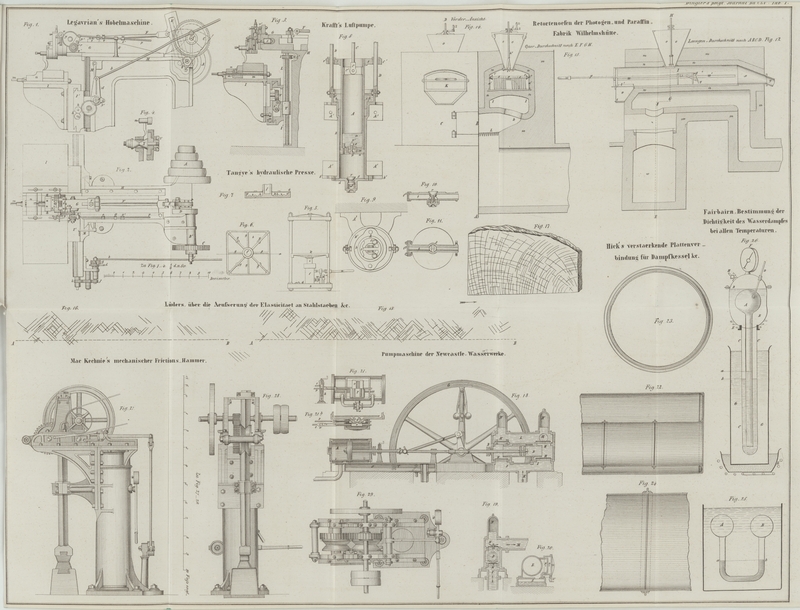
Um das Princip des Sättigungsmessers zu verstehen, denke man sich zwei Kugeln A und B (Fig. 25) durch eine
gebogene Röhre, welche bis a, b mit Quecksilber gefüllt
ist, verbunden und in ein Bad gesetzt, worin sie auf jede erforderliche Temperatur
erhitzt werden können. In jeder Kugel sey eine Toricellische Leere hergestellt
worden, und man habe 20 Gran Wasser in A, und 30 oder 40
in B gebracht. Angenommen nun, die Temperatur werde
langsam und gleichförmig um diese Kugeln herum erhöht, so wird das Wasser in jeder
derselben verdampfen und sie mit Dampf füllen, dessen Dichtigkeit der angewandten
Temperatur entspricht und mit deren Steigen größer wird. Zuletzt wird ein Punkt
eintreten, wo sämmtliches Wasser in der Kugel A in Dampf
verwandelt ist, und bei diesem Punkte wird die Quecksilbersäule bei a steigen und bei b sinken.
Dieß ist das Zeichen der Sättigung; so lange nämlich die Verdampfung in beiden
Kugeln A und B vor sich geht
und die Temperatur eine gleichförmige ist, wird jede Kugel Dampf von gleicher
Spannung enthalten und die Quecksilbersäulen a und b werden auf gleicher Höhe bleiben; sobald aber das
Wasser in A verdampft ist und der Dampf anfängt
überhitzt zu werden, hört der Druck in A auf mit dem in
B gleich zu seyn und die Quecksilbersäule wird
sogleich fallen und so die Differenz anzeigen. Durch die plötzliche Veränderung des
Quecksilberstandes wird der Punkt angezeigt, bei welchem die Temperatur des Bades
mit dem Sättigungspunkte des Dampfes in A
correspondirt.
Als Beweis für die Empfindlichkeit dieser Probe führe ich an, daß bei 290° F.
die Quecksilbersäule für jeden Temperaturgrad über dem Sättigungspunkte um beinahe
zwei Zoll steigen würde, weil dann die Druckzunahme in Folge der Verdampfung
zwölfmal so groß ist als diejenige in Folge der Expansion beim Ueberhitzen, und eine
ähnliche Differenz findet bei anderen Temperaturen statt.
Der zu den Versuchen dienende Apparat erhält je nach dem beabsichtigten Drucke und
anderen Umständen eine verschiedene Einrichtung. Fig. 26 stellt eine
Anordnung desselben dar, welche mit Erfolg benützt wurde. Sie besteht in einer
Glaskugel von ungefähr 70 Kubikzoll Inhalt, in welche, nachdem darin eine
Toricellische Leere erzeugt wurde, die gewogene Wassermenge eingebracht wird. Die
mit einem Stiel versehene Kugel A ist von einem
kupfernen Kessel B, B umgeben, welcher durch eine starke
Glasröhre C, C verlängert ist, die den Stiel der Kugel
einschließt. Der kupferne Kessel bildet das Wasser- und Dampfbad, durch
welches die Kugel erhitzt wird und entspricht der zweiten Kugel B in der ersten Figur. Die bewegliche Quecksilbersäule
oder der Sättigungsmesser ist unten in der Röhre C, C
angebracht, und der Sättigungspunkt wird durch das Steigen der innern
Quecksilbersäule a und das gleichzeitige Fallen der
äußern Quecksilbersäule b angezeigt. Sobald sämmtliches
Wasser in der Kugel A verdampft ist, steigt die innere
Quecksilbersäule augenblicklich um das Gleichgewicht des Druckes herzustellen, und
zwar zunehmend mit der Temperatur-Erhöhung.
Der Kessel kann bei E durch Gasstrahlen erhitzt werden
und ist mit einem offenen Oelbade G versehen, um die
Glasröhren auf derselben Temperatur wie den Kessel zu erhalten; dieses Oelbad ist
auf ein Sandbad gesetzt und wird ebenfalls durch Gas erhitzt. Ein Thermometer D zeigt die Temperatur und ein Manometer F den Druck des Dampfes an; mittelst eines Ausblasehahns
H kann die Temperatur nöthigenfalls vermindert
werden.
Wir haben bereits eine Anzahl von Resultaten erzielt, aber sie sind noch nicht
genügend vorgeschritten, um veröffentlicht zu werden.
Die folgenden Zahlen wurden annähernd mittelst der obigen theoretischen Formel
berechnet und die durch Versuche erhaltenen Resultate denselben beigesetzt. Am
zweckmäßigsten wird die Dichtigkeit des Dampfes durch die Anzahl der Volume
ausgedrückt, auf welche sich das Wasser bei seiner Erzeugung ausgedehnt hat. So
verwandelt sich ein Kubikzoll Wasser in 1670 Kubikzoll Dampf von 212° F., in
882 Kubikzoll Dampf von 215° F., und in 400 Kubikzoll Dampf von 304°
F.; in dieser Weise wurden die folgenden Zahlen berechnet:
Dampfvolumen
Temperatur.
nach der Formel.
nach dem Versuch.
244° F.
1005
896
245° F.
969
890
257° F.
790
651
262° F.
740
680
268° F.
680
633
270° F.
660
604
283° F.
540
490
Diese Bestimmungen sind für die Pressungen von 10 bis 50 Pfd. Ueberdruck nicht genaue
Reductionen aus den Versuchsresultaten, sondern nur annähernde; sie zeigen aber
durchaus eine entschiedene Abweichung von dem Gesetze für permanente Gase, in dem
schon von Prof. Thomson angegebenen Sinne; die
Dichtigkeit ist nämlich immer größer als sie die Formel ergibt.
Ich hoffe der nächsten Versammlung der Gesellschaft mit Hülfe meines Freundes Tate eine Reihe von Resultaten vorlegen zu können,
wodurch wir über den Werth
des überhitzten Dampfes vollkommen ins Klare kommen; wir werden nämlich seine
Dichtigkeit und sein Volumen im Vergleich zum Druck, bei allen Pressungen, von der
atmosphärischen bis zu 500 Pfd. auf den Quadratzoll, bestimmen.
––––––––––
Nach dem Vortrage dieses Berichtes machte Prof. Macquorn Rankine die Versammlung auf die Uebereinstimmung dieser Versuche mit der
mechanischen Wärmetheorie aufmerksam. Folgende Formel wurde zuerst aus den
thermodynamischen Principien von Prof. Clausius
abgeleitet:
v – v' = JL/(t
dp/dt),
worin v' das Volumen in Kubikfußen
von 1 Pfd. Wasser, bei einer gegebenen Temperatur ist; v
das Volumen in Kubikfußen von 1 Pfd. gesättigtem Dampf; L die latente Verdampfungswärme von 1 Pfd. Dampf, in gewöhnlichen
Wärmeeinheiten ausgedrückt; J
Joule's mechanisches Aequivalent einer Wärmeeinheit,
dessen Werth für Fahrenheit's Scala 772 Fußpfund ist; t
die absolute Temperatur = der Temperatur nach Fahrenheit's Scala + 461°,2;
und dp/dt das Verhältniß, in
welchem der Druck des gesättigten Dampfes sich mit der Temperatur ändert.
Hr. Rankine ließ vor einiger Zeit Tabellen über die
Dichtigkeit und das Volumen des Wasserdampfes für den praktischen Gebrauch drucken,
welche er in Ermangelung directer experimenteller Daten mittelst dieser
theoretischen Formel berechnete. Folgende Tabelle zeigt, daß die Resultate der
Formel nahezu mit jenen der Versuche von Fairbairn und
Tate übereinstimmen.
Verhältniß des
Dampfvolumens
zum
Wasservolumen
Temperatur.
nach der Theorie.
nach dem Versuch
244° F.
936
896
245° F.
920
890
257° F.
756
751
262° F.
698
684
268° F.
635
633
270° F.
616
604
283° F.
506
490
Wie man aus dieser Tabelle ersieht, sind die theoretischen Resultate immer größer als
die experimentellen, was sich vielleicht durch eine Differenz in dem angenommenen
Werthe für die Dichtigkeit des Wassers erklären läßt. Bei der theoretischen Berechnung wurde das Volumen
des Wasserdampfes mit dem kleinstmöglichen Volumen eines
gleichen Gewichtes Wasser verglichen, nämlich mit dem Volumen bei 39°,1
Fahr.
Tafeln