| Titel: | Ueber einen amerikanischen und einen englischen Vorschlag zu excentrischen Zügen für gezogene Feuerwaffen. |
| Autor: | Dy |
| Fundstelle: | Band 174, Jahrgang 1864, Nr. XXV., S. 89 |
| Download: | XML |
XXV.
Ueber einen amerikanischen und einen englischen
Vorschlag zu excentrischen Zügen für gezogene Feuerwaffen.
Mitgetheilt vom Artillerie-Hauptmann
Dy.
Mit Abbildungen auf Tab.
II.
Ueber einen amerikanischen und einen englischen Vorschlag zu
excentrischen Zügen für gezogene Feuerwaffen.
In dem Scientific
American vom 21. November 1863 findet sich unter der
Ueberschrift: „Die Züge gezogener
Gewehre“ eine mit G. Hagenmeyer unterzeichnete Zuschrift an den
Herausgeber des genannten Blattes, in welcher die Anwendung von Zugprofilen mit
excentrischer Basis bei Anfertigung von gezogenen Feuerwaffen folgender Weise
befürwortet wird:
„Wenn eine Kugel durch die Kraft des Pulvers im gezogenen Rohre in
Bewegung gesetzt wird, so hat sie das Bestreben geradlinig und ohne spirale
Bewegung vorwärts zu gehen; die Züge müssen sie also zu einer RotationUm ihre in der Längenachse des Rohres liegende Achse. zwingen, und hierbei wird auf einer Seite der Züge, welche ich die
SchneideNach deutscher Nomenclatur Führungsfläche der Züge. derselben nennen will, ein Druck entstehen, während zwischen dem
Geschosse und der anderen Seite der Züge, welche der RückenNach deutscher Nomenclatur Ladefläche der Züge.Anmerk. des Einsenders. derselben heißen mag, ein Zwischenraum entsteht, welcher, als Spielraum,
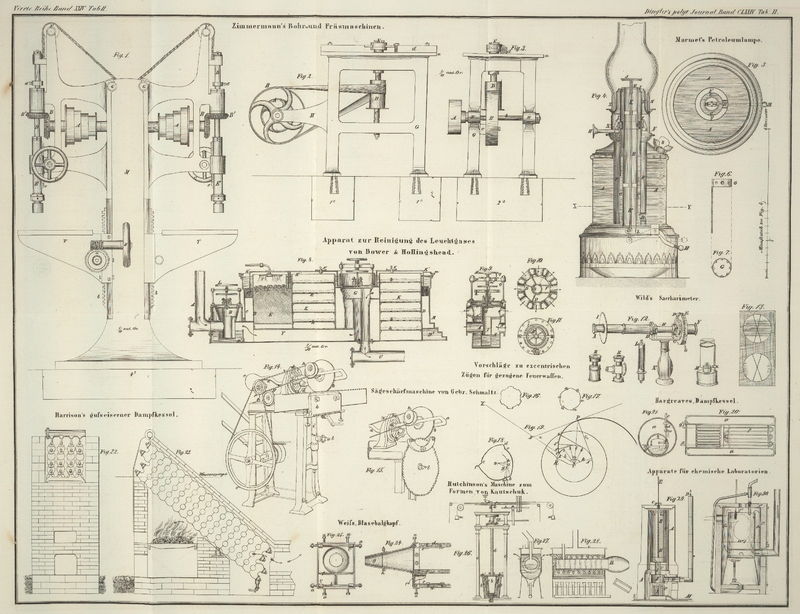
eine Pulvergasentweichung zur Folge hat. – Durch Züge der in Fig. 16
dargestellten Form wird hierbei auch noch eine ganz unnöthige Reibung des
Geschosses auf dem Boden der Züge erzeugt und es macht diese Zugform, welche man
gewöhnlich angewendet findet, ferner eine bedeutende Tiefe der Züge nothwendig,
wenn dem Projectile durch die Schneiden der letzteren ein genügender Antrieb zur
Notation gegeben werden soll.“
„Die Form der Züge würde also besser der in Fig. 17 dargestellten
zu entsprechen haben, bei welcher die mit a
bezeichneten Stellen als die Schneiden der Züge dastehen, das Geschoß also während
seiner Vorwärtsbewegung zur Rotation zwingen, und ferner Boden und Rücken der
Züge von einer Form sind, welche das Geschoß nach Möglichkeit vor Frictionen
sichert, ohne deßhalb den Spielraum unnöthig groß werden zu lassen.“
„Ich habe mancherlei Büchsen mit Zügen von der Form Fig. 16 gesehen,
welche, wenige Schüsse ausgenommen, nur sehr ungenau schossen. – Sind
diese Züge zu flach, so folgt ihnen die Kugel nicht, und sind sie zu tief, so
werden dadurch nicht nur Bewegungshindernisse des Geschosses hervorgerufen,
sondern es wird auch ein steter Spielraum erzeugt, während angestellte Versuche
mit neu angefertigten und mit abgeänderten Büchsen von der in Fig. 17 dargestellten
Form des Zugprofiles diese als die beste haben erkennen lassen.“
Noch bestimmter wird diese Forderung eines Zugprofiles mit excentrischer Basis ferner
in Newton's
London Journal of arts vom 1. Februar 1864 durch
Veröffentlichung eines Patentes formulirt, welches an Theophilus Alexander Blakely in London (Montpelier-square) am 22. Mai 1863 für „eine neue Methode
Geschütze zu ziehen und deren Geschosse damit übereinstimmend
einzurichten“ ertheilt worden ist.
Dieser Erfindung nach sollen nämlich „Zugprofil und Geschoßform so
eingerichtet werden, daß die drehende Kraft, an irgend einem Punkte des
Geschosses angreifend, immer dieselbe Wirkung äußere“ und als hierzu
führende Regel wird dann Folgendes angegeben:
„Man bestimme zuerst diejenige Entfernung vom Mittepunkte des Projectiles,
in welcher die drehende Kraft wirksam seyn wird; – je kleiner das Kaliber
ist, desto näher liegt dieser Angriffspunkt am Centrum. Dann beschreibe man
einen Kreis, welcher seinen Mittepunkt in der Rohrachse und zum Radius die oben
bezeichnete Entfernung hat, und gebe hiernach den Zügen eine solche Gestalt, daß
jede senkrecht auf ihrer Oberfläche stehende Linie eine Tangente an den so
beschriebenen Kreis ist, wie dieses durch die in Fig. 18 gegebene
Zeichnung veranschaulicht wird, in welcher a b, c d
und e f die Führungsflächen (bearing surfaces) der Züge sind. Die zu diesen Führungsflächen
senkrecht stehenden Linien a g, h i, b k sind alle
gleichweit vom Centrum o entfernt. – Die
Formen der Geschosse stimmen dann hiermit überein, indem auch bei deren
Oberflächenbildung nach denselben mathematischen Regeln verfahren
wird.“
Die anscheinende Verschiedenheit, welche bei Vergleichung der Hagenmeyer'schen Zeichnung Fig. 17 und der Blakely'schen Zeichnung Fig. 18 darin liegt, daß
die Führungsflächen der zur oberen Rohrhälfte gehörigen Züge in ersterer Zeichnung
den linken und in letzterer Zeichnung den rechten Theil der Zugrinne bilden, wird
sofort verschwinden, wenn
man entweder, – bei gleichbleibendem Standpunkte des Beobachters am hinteren
Ende des dort abgeschnittenen Rohres – den Blakely'schen Zug als für ein schraubenrechts und den Hagenmeyer'schen Zug als für ein schraubenlinks gezogenes Rohr bestimmt
betrachtet, oder auch, wenn von der Annahme ausgegangen wird, der Blakely'sche Zug werde von der Mündung und der Hagenmeyer'sche Zug vom Ladungsraume eines
schraubenrechts gezogenen Rohres aus beobachtet. Die das Spitzgeschoß zur Rotation
um seine Längenachse zwingenden Führungsflächen der Züge bilden nämlich, ihrer
Bestimmung gemäß, von der Mündungsfläche eines schraubenrechts gezogenen Rohres aus
betrachtet, bekanntlich in der oberen Rohrhälfte stets die rechten Seitenflächen der
Zugrinnen eines schraubenrechts gezogenen Rohres, während die Ladeflächen derselben,
– an denen die mit Führungszapfen oder Führungsleisten versehenen Geschosse
eines gezogenen Vorderladungsrohres in den Laderaum des letzteren hinabgleiten
–, in diesem Falle am rechten Zugrinnen-Rande liegen.
Ihrem Sinne nach stimmen beide Vorschläge also vollkommen darin überein, daß
Zugprofile mit concentrisch zum Kaliberkreise geführter Basis und radial zu diesem
Kreise liegendem Durchschnitte der Zug-Seitenflächen nicht zu empfehlen sind,
vielmehr Zugprofile mit excentrischer Basis zur Anwendung kommen müssen, für welche
bekanntlich auch schon von Deutschland und Frankreich aus mannichfache Vorschläge
geliefert worden sind.Vergleiche: Rutzky, die Einrichtung und die
Construction gezogener Geschütze, S. 32 bis 47.
In Bezug auf Bestimmtheit der Ausführungsvorschriften aber steht der Hagenmeyer'sche Vorschlag, welcher nur das ungefähre Bild
eines empirisch gut befundenen Zugprofiles liefert, der genau präcisirten Forderung
Blakely's entschieden nach, welche letztere, den
Terminologien der Mechanik und der analytischen Geometrie entsprechend ausgedrückt,
nichts anderes besagt, als: das senkrecht zur Rohrachse stehende Zugprofil soll die
Evolvente eines Kreises seyn, welcher seinen Mittepunkt in der Rohrachse und zum
Radius eine Länge hat, deren Maaßzahl man erhält, wenn das Drehungsmoment des um
seine Längenachse rotirenden Geschosses durch dessen Masse dividirt und aus dem so
entstehenden Quotienten dann die Quadratwurzel gezogen wird.
Blakely's Vorschlag weist also für die Gestaltung des
Zugprofiles gezogener Feuerwaffen ganz auf dieselbe Curve hin, welche die Mechanik
bereits zur Anwendung bringt, wenn es sich darum handelt, die Kämme einer gezahnten Stange nach
einem gegebenen Grundkreise zu krümmen, oder auch die Hebedaumen eines Stampfwerkes
so einzurichten, daß der verticale Stampfer dadurch gleichförmig gehoben und
zugleich auch die Entfernung des Angriffspunktes der hebenden Kraft vom Schwerpunkte
des Stampfers nicht geändert werde, und es bestimmt dieser Vorschlag dann auch noch
weiter, daß der Radius des dem Zugprofile als Evolute dienenden Grundkreises gleich
k seyn soll, wenn das Drehungsmoment des
zugehörigen, um seine Längenachse rotirenden Geschosses von der Masse M gleich Mk²
gefunden worden ist.
Erscheint es demnach zulässig, die hier in Frage kommenden Langgeschosse der
einfacheren Rechnung wegen als massive oder hohle Cylinder homogener Masse ansehen
zu dürfen, so ist der Radius des dem Zugprofile als Evolute dienen sollenden
Grundkreises für ein Vollgeschoß vom Kaliberhalbmesser R
gleich R√1/2 und für ein Hohlgeschoß desselben
Kalibers gleich √(R² + r²)/2 zu setzen, wenn die innere Geschoßhöhlung
den Halbmesser r hat; denn es ist in diesem Falle das
Drehungsmoment des massiven Cylindergeschosses gleich 1/2 MR² und das des hohlen Geschosses derselben
Art gleich 1/2 M¹ (R² + r²) wenn M und M¹ in beiden Fällen das Product
VD aus dem Volum V
und der Dichtigkeit D der homogenen Geschoßmasse
bedeuten.
Sollen, nachdem dieser Halbmesser k des Grundkreises in
der einen oder in der anderen Weise, bestimmt worden ist, die Punkte der das
Zugprofil zu bilden habenden Kreis-Evolvente dann durch Rechnung festgelegt werden, und bedient man sich hierzu eines
rechtwinkeligen Coordinatensystemes, dessen Abscissenachse CX, Fig. 19, radial zum
Grundkreise liegend, durch den Anfangspunkt A der Curve
geht, so ist der dahin abzielenden Rechnung am einfachsten wohl die als
Constructionsbedingung gegebene Länge des Krümmungsradius ρ der Evolvente zu Grunde zu legen, welche für ein dem Centriwinkel
ω entsprechendes Peripheriestück kω des abgewickelt werdenden Grundkreises
ebenwohl immer:
ρ = kω
seyn muß. – Combinirt man nämlich hiermit die
allgemeine Gleichung für den Krümmungsradius irgend einer Curve von bekanntem
Bildungsgesetze:
ρ = – ds/dα
Vergleiche: Vega, Vorlesungen über die höhere
Mathematik, Bd. II S. 529.,
in welcher ds das Differenzial des
Curvenbogens und α den Tangenten-Winkel
irgend eines Curvenpunktes P bezeichnen, so ist in
diesem besonderen Falle also
ds/dα = – kω
und da ferner auch für die zum Punkte P der Curve gehörige Abscisse und die zugehörige Ordinate y
Textabbildung Bd. 174, S. 93
ist, so erhält man hieraus die Gleichung
dx/cos
α dα = – kω
in welcher, weil für irgend ein, dem Centriwinkel ω des Grundkreises entsprechendes
Peripheriestück, kω = AA¹ desselben, die Tangente PN des zu diesem abgewickelten Bogen gehörigen
Evolventen-Punktes P, dem zweiten Schenkel CA¹ dieses Centriwinkels parallel seyn
muß:
α = 180° – ω
und folglich
cos α = – cos ω
zu setzen ist, so daß hieraus das Differenzial der Abscisse
x:
dx = kω . cos ω . dω
und die Abscisse selbst:
x = ∫ k
ω . cos ω d ω = k ∫ ω . cos ω d ω
gefunden wird, und endlich da
∫ ω cos ω d
ω = ω sin ω –
∫ sin ω d ω = ω sin ω + cos
ω
gefunden wird,
x = k .
cos ω + k ω sin
ω + C
folgt, in welcher Gleichung die Constante C der Integration, für Abscissen welche vom Mittepunkte
des Grundkreises an gemessen werden, gleich Null ist, weil in diesem Falle für ω gleich Null, die Abscisse x gleich dem Radius k des
Grundkreises ist, obige Gleichung also in:
k = k + 0
+ C
übergeht, woraus
C = 0
folgt.
Für vom Centrum des Grundkreises an gemessene Abscissen ist also, wenn der Radius
dieses Grundkreises gleich k ist, die Abscisse irgend
eines Punktes P der Curve:
x = k .
cos ω + k ω sin
ω
und in ganz analoger Weise findet man für die zur Abscisse x gehörige Ordinate y
desselben Punktes P den Werth:
y = k sin
ω – k ω cos ω,
wornach also jeder Punkt dieser Kreis-Evolvente durch
Rechnung bestimmt werden kann.
Zu einer graphischen Festlegung der hier in Rede stehenden
Curve aber können nach dem Vorhergehenden folgende Constructions-Methoden
angewendet werden:
1) Durch Punkte, indem man die Peripherie des als Evolute
gegebenen Grundkreises von irgend einem Punkte A
derselben an, siehe Fig. 19, in so kleine und einander gleiche Theile eintheilt, daß jeder
derselben ohne Nachtheil mit feiner Sehne verwechselt werden kann, und dann in allen
diesen Theilpunkten 1, 2, 3, 4 etc. Tangenten errichtet, auf denen die
beziehungsweisen Längen 11' = A 1, 22' = 2 A 1, 33' = 3 A 1 etc.
abgeschnitten werden.
Die so bestimmten Endpunkte 1', 2', 3', 4' etc. dieser Tangentenlängen sind dann
Punkte des als Evolvente dieses Grundkreises gesucht werdenden Zugprofiles.
2) Durch kleine Kreisbögen, indem man mittelst der ad 1 bestimmten Tangentenlängen 11' = A 1, 22' = 2 . A 1, 33' = 3.
A 1 etc. die kleinen Kreisbögen A 1', 1'2', 2'3', 3'4' etc. beschreibt und die Curve so
zusammensetzt.
3) Durch einen einzigen zusammenhängenden Zug, indem man
um den mittelst einer Metallplatte etc. dargestellten Grundkreis einen biegsamen und
undehnbaren Fäden legt, welcher hiernach so von der Peripherie desselben abgewickelt
wird, daß er dabei immer straff angezogen bleibt. – Der Fäden wird dann, wenn
er z.B. bis zum Theilpunkte 3 der Fig. 19 abgewickelt
worden ist, eine Tangente von der Länge A 3 = 3 . A 1 = 33' an den Grundkreis bilden, 3' also ein Punkt
der darzustellenden Curve seyn u.s.w.
Faßt man weiter auch die Entfernung E = CP in's Auge, welche ein dem Abwickelungswinkel
ω des Grundkreises entsprechender
Evolventenpunkt P vom Centrum C der Evolute haben wird, so ist dieselbe, wenn der zum Curvenpunkte P gehörige Krümmungsradius mit ρ und der Halbmesser des Grundkreises mit k bezeichnet werden:
E = √(k² + ρ) = √(k² + (kω)²) = √(1 + ω²).
Für denselben Abwickelungswinkel ω, aber den Halbmesser k¹ des Grundkreises wird diese Entfernung also seyn:
E¹ = k¹ √(1 + ω²)
und es verhalten sich diese Entfernungen E und E¹ also zu
einander wie die Radien k und k¹ der zugehörigen Grundkreise, woraus hervorgeht, daß diese
Kreisevolvente um so stärker von der Peripherie ihres Grundkreises abgebogen seyn
wird, je größer der Radius k des letzteren ist.
Da nun nach dem Vorhergegangenen der Radius des Grundkreises, welcher als Evolute des
Zugprofiles einer Feuerwaffe dienen soll, für cylindrische Vollgeschosse homogener
Masse gleich R√1/2 und für dergleichen
Hohlgeschosse gleich √(R² + r²)/2 ist, wenn R den
Kaliberhalbmesser und r den inneren Höhlungsradius
derselben bezeichnen, so verhalten sich in diesem Falle die Entfernungen E und E¹ der,
gleichen Abwickelungswinkeln der Grundkreise entsprechenden Zugprofilspunkte:
Textabbildung Bd. 174, S. 95
Die Führungsflächen der Züge müssen, diesem Gesetze entsprechend, demnach für
Hohlgeschosse homogener Masse stärker von der cylindrischen Fläche der
Kaliberbohrung abgebogen werden, als dieses für Vollgeschosse derselben Art
erforderlich ist, und zwar in einem Verhältnisse, welches um so größer ist, je
hohler die Geschosse sind.
Früher ist in diesem JournaleIm „artilleristischen Nachtrag zu Anderson's Anwendung des Copir- oder
Uebertragungs-Principes bei der Anfertigung und beim Ziehen von
Feuerwaffen,“ Bd. CLXIX S. 92. schon einmal darauf hingedeutet worden, daß für Hohlgeschosse irgend eines
Kalibers auch der Drall des Zuges ein anderer als der für Vollgeschosse homogener
Masse desselben Kalibers bestimmte seyn müsse, wenn dabei von der Bedingung
ausgegangen wird, daß das zwischen den lebendigen Kräften der anfänglichen Rotation
und der anfänglichen fortschreitenden Bewegung des Geschosses bestehende Verhältniß constant
seyn soll. – Legt man, um die Wirkungen dieses Gesetzes auf
Constructionsfragen in Parallele mit denen des obigen zu stellen, auch hier die
Rechnung an, so ist der Verhältnißquotient Q der
genannten lebendigen Kräfte nach Bd. CLXIX S. 100 dieses Journals für cylindrische
Vollgeschosse homogener Masse vom Kaliber-Radius R und für die Drall-Länge H des
zugehörigen Rohres:
Q = 4,935 . (2R/H)² = 19,74 R²/H²
wenn dabei, weil es sich hier nur um Vergleichung dieser
Quotienten für Voll – und Hohlgeschosse derselben Materie handelt, von der
Schwere der Masseneinheit abgesehen wird, welche letztere nach dem französischen
Maaßsysteme bekanntlich gleich ebenso vielen Kilogrammen ist, als die Beschleunigung
der Schwere, g, in Metern beträgt.Vergleiche: Duhamel. Lehrbuch der analytischen
Mechanik, Bd. I S. 304.
Für ein cylindrisches Hohlgeschoß homogener Masse desselben Kalibers mit dem
Höhlungsradius r und der Drall-Länge des
zugehörigen Rohres gleich H' beträgt dieser Quotient Q' nach demselben Entwicklungsgange ferner:
Q¹ = 19,74 . (R² + r²)/H¹ ²
und sollen diese Quotienten also gleich bleiben, mithin
Q = Q¹
seyn, so erhält man zur Bestimmung des dieser Bedingung
entsprechenden Drall-Längen-Verhältnisses die Gleichung:
19,74 . R²/H² = 19,74 . (R² + r²)/H¹ ²
woraus die Proportion
H : H¹ = R : √(R² + r²) = 1 : √(1 + (r/R)²)
hervorgeht, durch welche also besagt wird, daß nach diesem
Gesetze die für cylindrische Vollgeschosse homogener Masse gültigen
Drall-Längen bei Anwendung von Hohlgeschossen derselben Art immer größer
werden müssen, je hohler die zum Gebrauche kommenden Projectile sind.
Zwischen den beiden hier vorliegenden Gesetzen besteht also der interessante
Zusammenhang daß, wenn Zugprofil und Drall-Länge für ein massives
Cylindergeschoß homogener Masse irgend eines Kalibers festgestellt worden sind, bei Anwendung eines dergleichen Hohlgeschosses von gegebener
Cavität dann die Zugprofile ganz in demselben Verhältnisse
excentrischer werden müssen, in welchem die Drall-Längen zuzunehmen
haben.
Tafeln