| Titel: | Die Zeichen-Instrumente „Radial“ und „Radiarc“ des Architekten Prof. L. Bohnstedt in Gotha. |
| Fundstelle: | Band 174, Jahrgang 1864, Nr. LV., S. 185 |
| Download: | XML |
LV.
Die Zeichen-Instrumente
„Radial“ und „Radiarc“ des Architekten
Prof. L. Bohnstedt in
Gotha.
Mit Abbildungen auf Tab.
III.
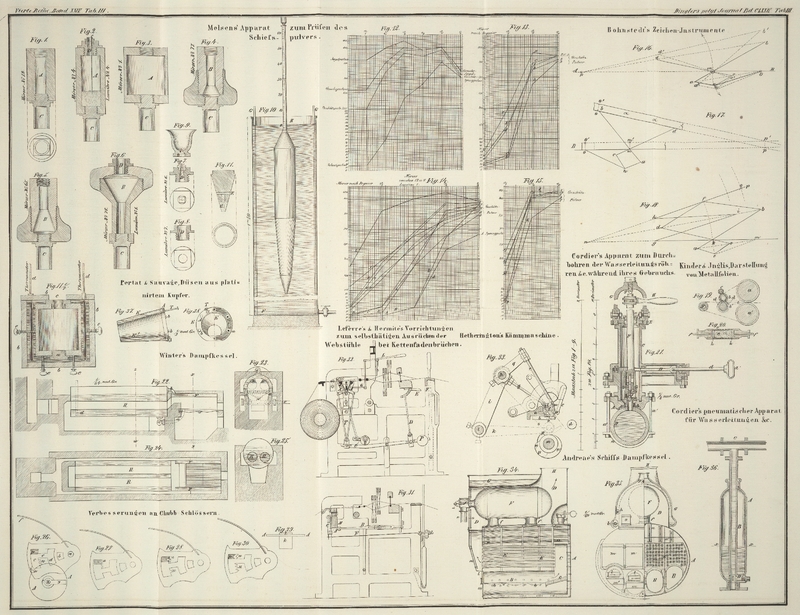
Bohnstedt's Zeichen-Instrumente.
1. Der Radial (Fig. 16 und 17).
Angenommen: In Fig.
16 sey die gerade Linie ab = Linie cd, und die Entfernung von ihrem
gemeinschaftlichen Schnittpunkte m, ma = mc; ferner an = cn = am = cm; endlich die Linie mo
(welche durch den Schnittpunkt
m geht) = no.
Die Linie ac, nach o hin
verlängert, halbirt das Viereck amon (die Dreiecke amo und an
o sind congruent; ebenso die Dreiecke amc und anc,
weil sie gleiche Seiten haben). Werden die Linien mo und
bd verlängert, bis sie sich in p schneiden, so entstehen zwei ähnliche Dreiecke amo und bmp, bei welchen die
Linien ao und bp
parallel sind, denn dm = mb, am = mc, Winkel pmb = (Winkel pmd + Winkel
dmb) = Winkel amo =
(Winkel cmo + Winkel amc).
In den beiden Dreiecken pmb
und
amo
verhält sich mp zu mo, wie bm zu ma
.
Ist das Verhältniß von am zu mb gegeben und auf der Linie AB die
Entfernung des Punktes p von m bekannt (p bezeichnet den Punkt, in welchem
oberhalb AB zu ziehende gerade Linien sich
schneiden sollen), so ist umgekehrt der Punkt 0 zu finden, indem mo = (pm . am)/mb gesetzt wird. o ist der Punkt auf AB, um welchen mit dem Radius mo (= no) ein Bogen beschrieben werden kann, worin der Punkt
n sich bewegen wird. Je weiter n von m gerückt wird, um so
mehr werden die Punkte a und c genähert (bis sie ganz zusammenfallen) und ebenso die gegenüberliegenden
Punkte b und d (siehe Fig. 16
ma', me', a'n', c'n', md' und mb'). Sämmtliche gerade Linien aber, welche Verlängerungen von den Linien
bd, b'd' etc. sind, werden in p die Linie AB schneiden, d.h. werden
Radien zu Kreisen seyn, welche den Punkt p zum Centrum
haben.
Das InstrumentIn einigen Theilen ein Storchschnabel., welches „Radial“ (von radius) genannt ist, beruht auf obigen Sätzen, und bezweckt, das Zeichnen
von geraden Linien zu ermöglichen, welche nach einem gemeinschaftlichen
Schnittpunkte (Centrum) gerichtet sind, solches auch dann, wenn dieser Schnittpunkt
außerhalb des Reißbretes liegt, ein Fall, der namentlich beim Ausführen von
perspectivischen Darstellungen mit fernliegenden Verschwindungspunkten nur zu oft
vorkommt. Dieses Instrument soll bei dergleichen Arbeiten das mühsame und
zeitraubende Ausmessen mit dem Proportionalzirkel, und das von Hrn. Professor Streckfuß angegebene sehr sinnreiche Verfahren mit dem
bogenförmigen Pappdeckelausschnitt (der für jeden neuen Verschwindungspunkt immer
neu herzustellen ist) ersparen, und namentlich für jeden beliebigen
Verschwindungspunkt (selbstverständlich innerhalb gewisser Grenzen) verwendbar
seyn.
Der „Radial“, Fig. 17, besteht aus vier
Metall-Schienen ab, cd, an und nc, welche in den Punkten a, m,
c und n mit einander drehbar verbunden sind,
und aus einer Schiene mB, auf welcher in m der Drehpunkt für ab und
c
d fixirt ist (oder fixirt werden kann)Die Einrichtung ist so getroffen, daß das Gestell mit dem Drehpunkt m entweder in der Mitte der Schiene, oder auf
einem der beiden Enden derselben festgeschraubt werden kann., ebenso wie der Punkt o auf derselben sich
fixiren läßt, um die Leitstange no, welche in n mit an und cn verbunden ist und durch eine Stellvorrichtung bei n geht, beliebig länger oder kürzer stellen zu können.
Ferner sind die beiden Enden b und d durch eine Stange in der Weise mit einander verbunden,
daß entweder b oder d auf
der Stange beweglich bleibt. Diese Stange endlich ist mit einer Schiene in
Verbindung gesetzt, unter welcher (vermittelst Heftzwecken) ein Lineal αα befestigt werden kann.
Wird die Schiene mB auf der Zeichnung
festgehaltenUm die Schiene nicht mit der Hand halten zu müssen, sind dem Instrumente zwei
Messingschienen beigelegt, welche mit dem einen Ende vermittelst je zweier
Zapfen an die Schiene AB fixirt werden,
und mit dem anderen Ende durch dazu gehörige Schraubzwingen an das
Zeichenbret sich befestigen lassen. und die durch b und d gehende Stange dem Punkte m genähert (oder,
umgekehrt, entfernt), so wird das Lineal auf der Zeichnung mit fortbewegt und erhält
dabei beständig eine solche Richtung, daß an ihm hin die gewünschten radialen Linien
mit Sicherheit gezogen werden können.
Anmerkungen: 1) Auf der ersten Linie, welche auf dem Papiere als Ausgangslinie
gezeichnet wird, muß ein Punkt in (am sichersten über m)
angemerkt und dann auch auf dem Lineale bezeichnet werden, um, wenn das Instrument
weggenommen worden und es wieder benutzt werden soll, dasselbe sogleich richtig an
die Ausgangslinie stellen zu können. Beim Beginne des Zeichnens müssen m und n übereinander zu
liegen kommen, und auf dem Lineale der Ausgangspunkt lothrecht über m, an der Kante des Lineals angegeben werden, entlang
welcher die Linien gezogen werden sollen. 2) Die Breite des Lineals ist insofern zu
berücksichtigen, als die Entfernung der zu benutzenden Kante desselben von den
Punkten m und o auch die
Entfernung des Punktes p' lothrecht (soweit das
Instrument überhaupt handlich ist) über p ergibt. 3)
Sind m und n, wie das
anfänglich stets der Fall seyn muß, übereinander befindlich, so muß der Zeichner den
Beginn der richtigen Bewegung des Instrumentes dadurch hervorbringen, daß er den
Drehpunkten n und m durch
eine auseinanderschiebende Bewegung vermittelst der Finger die erforderliche
Richtung gibt. – Kleine andere Handgriffe beim Gebrauche des Instrumentes
besonders anzugeben, wird nicht nöthig seyn, da es doch nur von solchen Personen
verwendet wird, deren Beschäftigung den erforderlichen Scharfblick für dergleichen
Dinge voraussetzen läßt.
2. Der Radiarc (Fig. 18).
Angenommen: Die in k (Fig. 18) sich
schneidenden geraden Linien ab und cd sind gleich lang, ferner ak = kc = ae = ce, dann kd = kb = df = bf: km = em, ferner kg = fh, und gi = hi.
Wird die Linie mk über g hinaus verlängert und ebenso die Linie bd, bis sie mit der Linie mg in n sich schneidet und f mit
n verbunden, so wird die Linie fn parallel seyn der Linie
em und die Entfernung des Punktes m von k, km, sich
verhalten zur Entfernung des Punktes n von k, zu nk, wie ak zu kb (oder
ck zu kd). Da km = me, und ke = ce = ae = ak, so sind die
Dreiecke amk und aem
congruent, ebenso die Dreiecke kcm und ecm (wegen der Gleichheit ihrer Seiten). Dasselbe findet
mit den Dreiecken nbk und nbf und den Dreiecken ndk und ndf statt. Das Dreieck akm
aber ist ähnlich dem Dreieck bkn (da dk = kb, ak = kc, Winkel dkb = Winkel akc und demzufolge auch der Winkel bnk = Winkel amk), demnach
sind die den gleichen Winkeln entsprechenden Seiten dieser Dreiecke
proportional.
Hieraus ergibt sich, daß die Linie nf
parallel
em, und nf = nk seyn müsse. Der Punkt n
wird somit zum Centrum eines Kreisbogens, der von k aus
gezogen den Punkt f in sich enthalten wird. Ist bn die gerade Linie, welche durch die beiden Punkte b und d geht und das
Parallelogramm kdfb halbirt, ist ferner der Punkt i in dieser Linie, so wird das Dreieck ign congruent dem Dreieck ihn seyn, weil hi = gi, in gemeinschaftlich und Winkel hin =
Winkel gin (Letzteres aus der Congruenz der Vierecke hibf und gibk zu ersehen,
bei denen, außer den vier gleichen Seiten, noch die Winkel ibf und ibk gleich sind).
Auf oben Gesagtem beruht die Einrichtung des Instrumentes,Ein Storchschnabel, bezüglich einiger Theile. welches „Radiarc“ (von radius und arcus) genannt
wurde und dazu dienen soll, beim Zeichnen und Darstellen solcher Kreisbogentheile
und dazu gehöriger Radien verwendet zu werden, deren Centren außerhalb des Zeichenbretes sich befinden,
und namentlich vorläufig beim Entwerfen von verschiedenen Maschinentheilen sich
vortheilhaft erweisen wird.
Der Radiarc besteht im Wesentlichen aus den (Metall-) Schienen ad, cd, ae, ec, df, fb, fh, hi und ig, welche in den Punkten a, k,
b, e, c, d, f, h und i drehbar miteinander
verbunden sind, aus der Schiene gm, auf welcher die
Drehpunkte g und k sich
feststellen lassen, ferner der Punkt m sich fixiren
läßt, um die Stange em, die mit dem Drehpunkte e verbunden ist, beliebig lang bei m feststellen zu können, dann aus einer Stange db, die in d oder b, mit dem einen Drehpunkte d oder b verbunden ist, während der andere auf
ihr fortbewegt werden kann, und aus einer ähnlichen Vorrichtung, welche auch dem
Drehpunkte i eine Fortbewegung auf der Stange db gestattet. Endlich aus einer mit h und f fest verbundenen
Schiene, unterhalb welcher ein Lineal (mittelst Heftzwecken) befestigt werden
kann.
Wird die Schiene gm auf dem Reißbret festgehalten,Um dabei die linke Hand frei zu lassen, sind dem Instrumente zwei
schaufelartige Ansätze beigefügt, die mit je zwei Zapfen auf der Schiene gm befestigt, und dann durch Auflegen von
Gewichten (wie solche in den Ateliers der Maschinenzeichner als Beschwerer
gebräuchlich sind) auch auf dem Zeichenbrete fixirt werden können. und die Schiene hf mit dem an derselben
befindlichen Lineal dem Punkte k genähert (oder
umgekehrt von ihm entfernt), so wird das Lineal bei der Fortbewegung stets eine
solche Richtung annehmen, daß die längs der KanteDiese Kante ist dadurch, daß Stiftchen unter der Metallschiene vorstehen, an
welche anlehnend das Lineal fixirt wird, so gestellt, daß sie den
Drehpunkten f und h
entspricht. desselben auf dem Brete gezogenen Linien, fortgesetzt, auf einen
gemeinschaftlichen (außerhalb des Bretes befindlichen) Schnittpunkt zulaufen.
Gleichzeitig wird ein Zeicheninstrument (Bleistift, Ziehfeder etc.), an eine
beliebige Stelle des Lineals angehalten,Wird der Bleistift oder die Ziehfeder nicht an die Kante des Lineales
angehalten, welche der Linie fh entspricht,
sondern an die gegenüberliegende Kante, so muß der Zeichner die Breite des
Lineales mit in Rechnung ziehen, da die auf solche Weise gezogene Bogenlinie
zwar auch den Punkt
n zum Centrum hat,
als Radius aber, die Hypotenuse des Rechteckes, dessen eine
Kathete die, von der Stelle, wo der Bleistift an das Lineal
angehalten wird, auf die gegenüberliegende Kante des Lineales gezogene Lothrechte ist (also die Breite des Lineales),
während die andere Kathete der Entfernung dieser Lothrechten von dem Punkte
n gleichkommt.Die den Bogen entsprechenden Radien müssen demnach stets an der der Schiene
gm zugekehrten Linealkante gezogen werden,
wogegen die Bogenlinien durch Befestigung der Ziehfeder oder des
Bleistifthalters an der anderen Kante des Lineales gezeichnet werden
können.Die Ziehfeder ist mit einem Plättchen in Verbindung gebracht, welches
vermittelst der unter demselben befindlichen Stiftchen auf dem Lineal an
beliebiger Stelle fixirt werden kann. Bei kartographischen Arbeiten möchte
es von Nutzen seyn, mehrere solcher Ziehfedern zugleich in den gewünschten
Entfernungen anzubringen, wodurch dann gleichzeitig die Bogenlinien sich
zeichnen lassen etc. bei Fortbewegung des Lineales eine Linie beschreiben, welche mit einer
Kreisbogenlinie, von dem erwähnten Schnittpunkte als Centrum aus beschrieben,
zusammenfällt, d.h. die also dargestellte Linie wird eine Kreisbogenlinie seyn,
deren Centrum jener, außerhalb des Reißbretes liegende Schnittpunkt ist.
Da nk : km = kb : ak, so ist km zu finden, indem man km = nk ak/kb nimmt. Verhält sich ak : kb = 1: 3, so ist km = 1/3 nk; oder ak : kb = 1: 4, so ist km = 1/4 nk. Ist
demnach ein Bogen zu zeichnen, dessen Centrum von k um 6
Fuß entfernt seyn soll, und das Instrument so eingerichtet, daß ak : kb = 1: 3, so muß der
Punkt m von k = 1/3. 6 = 2
Fuß weit festgestellt werden.
Da das Lineal von h über f
hinaus (in f ist die Stelle, wo die verlangten 6 Fuß von
n ab sich ergeben) noch einige Fuß nach p hin hinausragen kann, so wird man, wenn die Entfernung
von f nach o = 2 Fuß ist,
durch Anhalten des Bleistiftes bei o, einen Bogen 6 + 2
= 8 Fuß Halbmesser, mit demselben Centrum n zeichnen,
und von jeder beliebigen Stelle dieses Bogens, indem man entlang der Kante des
Lineals eine Linie zieht, die der Tangente dieses Bogenpunktes entsprechende
Lothrechte (den Radius) darstellen können.
(Ist das Verhältniß von ak : kb = 1: 4 und mk = 2 Fuß, so wird fn = 8 Fuß und no = 10 Fuß,
also für Kreise von 20 Fuß Durchmesser genügend seyn.)
Das Anmerken des Punktes f
auf der ersten Linie, die gezeichnet wird, ist anzurathen, um, wenn das Instrument
weggenommen worden und dann wieder weiter benutzt werden soll, dasselbe sogleich
richtig an die erste Linie, die Ausgangslinie, stellen zu können.Herr Hofmechanicus H. Ausfeld in Gotha
(Schwabhäusergasse Nr. 8) hat die Ausführung von Radialen (à 20 Rthlr. mit Kästchen) und von
Radiarcen (à 25 Rthlr. mit Kästchen)
übernommen.
Gotha, im September 1864.
Tafeln