| Titel: | Geradführung von Peaucellier. |
| Fundstelle: | Band 217, Jahrgang 1875, S. 362 |
| Download: | XML |
Geradführung von Peaucellier.
Mit Abbildungen im Text und auf Taf. VII [a/4].
Peaucellier's Geradführung.
Das Princip dieses Mechanismus, welches von dem Erfinder Peaucellier, Oberstlieutenant des französischen Geniecorps, schon im J.
1864 aufgestellt worden war, läßt sich in seiner speciellen Anwendung zur
Geradführung bei Balanciermaschinen leicht mit Hilfe des beistehenden Holzschnittes
erklären.
Textabbildung Bd. 217, S. 362
Es sei BCDE ein gelenkig verbundenes System von vier
gleichlangen Seiten, A ein Fixpunkt, von dem zwei
Verbindungsstangen zu den Punkten B und E gehen, F endlich ein zweiter Fixpunkt, welcher durch eine
Stange mit dem dritten verbunden ist. Der vierte Punkt D des beweglichen Rhombus BCDE hat sodann
seinen geometrischen Ort in der geraden Linie
DG, senkrecht auf die Verbindungslinie AF der Fixpunkte, sobald die Distanz derselben:
AF gleich der Stangenlänge FC ist.
Um dieses zu constatiren, genügt der Beweis, daß die Projection AG von ACD, welche drei
Punkte selbstverständlich stets eine gerade Linie bilden, constant bleibt.
Beschreibt man zu diesem Behufe vom Fixpunkte F aus einen Kreis vom Radius FC, so schneidet derselbe, in Folge der gemachten Annahme, die Linie FG im Punkte A, und
verbindet man den zweiten Schnittpunkt H mit dem Punkte
C, so besteht in Folge der Aehnlichkeit der Dreiecke
ACH und AGD die
Relation
AC/AG = AH/AD oder AG × AH = AC × AD.
Nachdem jedoch AH = 2 × FC constant ist, so ist nur noch zu beweisen, daß AC × AD constant
bleibt, um auch die Unveränderlichkeit des Werthes von AG behaupten zu können.
Die Länge AC hat aber als Seite des
stumpfwinkeligen Dreieckes ACB den Werth
Textabbildung Bd. 217, S. 362
worauf sich sofort ergibt
Textabbildung Bd. 217, S. 362
somit constant, nachdem die Längen AB und BC unveränderliche
Größen sind.
Man erhält somit auf diese Weise eine vollkommen correcte Geradführung, welche sich
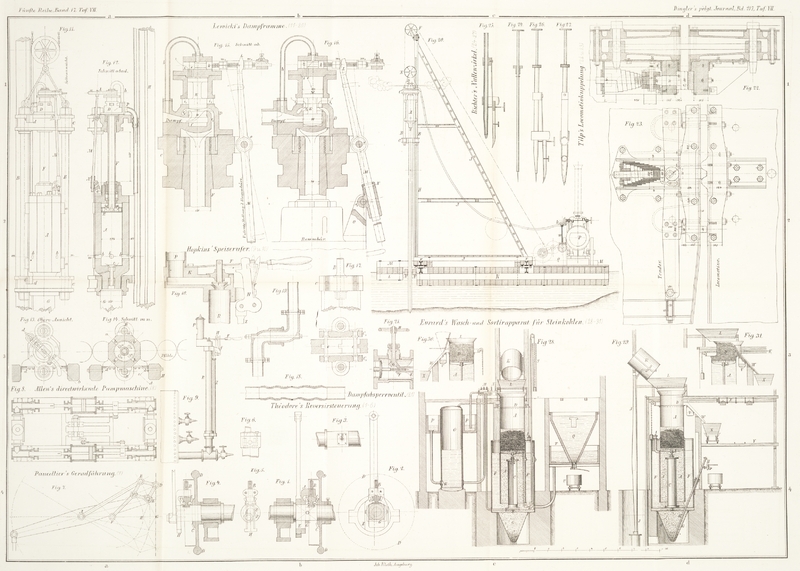
in vorzüglicher Weise, wie dies in Figur 7 ersichtlich ist, bei
Balanciermaschinen statt des nur annähernd richtigen Watt'schen Parallelogrammes
verwenden läßt.
Unsere Quelle (Bulletin de Mulhouse, 1875 S. 179 ff.)
bespricht auch noch weitere Anwendungen desselben Mechanismus zur Construction
verschiedener Curven, welche durch Veränderung der Länge CF erhältlich sind. Ein näheres Eingehen hierauf würde uns jedoch zu weit
führen; für den hier zunächst ins Auge gefaßten Zweck aber wird sich der vorliegende
Mechanismus gewiß rasch Bahn brechen, um so mehr als er selbst bei den ungünstigsten
Verhältnissen zwischen Balancier-Radius und Kolbenhub eine stets gleich correcte Geradführung ermöglicht.
Tafeln