| Titel: | Vorrichtung zum Anreissen von Kreisevolventen. |
| Autor: | V. Thallmayer |
| Fundstelle: | Band 228, Jahrgang 1878, S. 16 |
| Download: | XML |
Vorrichtung zum Anreiſsen von
Kreisevolventen.
Mit Abbildungen auf Tafel
2.
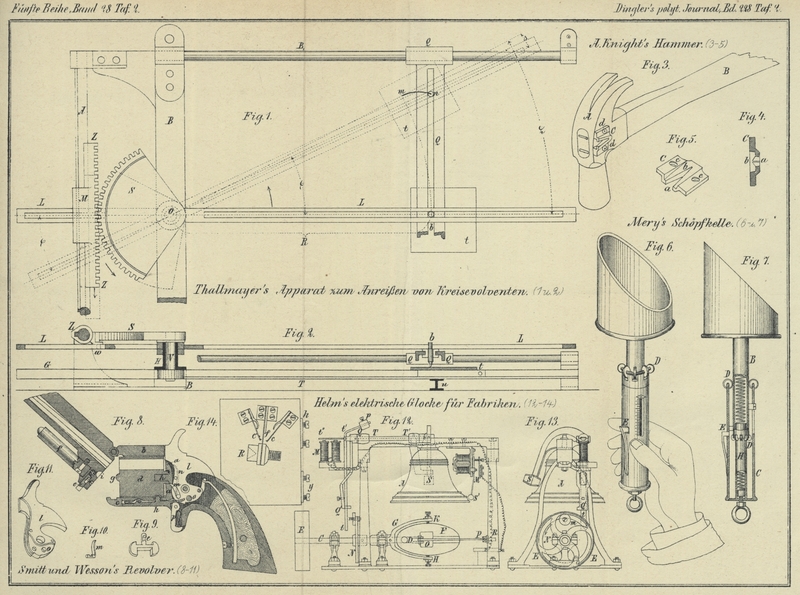
Thallmayer's Vorrichtung zum Anreiſsen von
Kreisevolventen.
Im Anschlusse an die S. 22 des vorhergehenden Bandes beschriebene Baffrey'sche Vorrichtung zum Anreiſsen von
Zahnschablonen erlaube ich mir im Nachfolgenden ein Instrument zu beschreiben, mit
welchem Kreisevolventen in solcher Länge, wie man sie für Verzahnungen benöthigt,
angerissen werden können; dasselbe ist in Fig. 1 und 2 Taf. 2 dargestellt.
Der Verticalzapfen V kann sich in einem vom Bügel B aufsteigenden Halslager H drehen; das obere Ende desselben trägt ein gezahntes Segment S, das untere hingegen eine Schiene TG, deren Theil T zur
Aufnahme einer kleinen Tafel t dient, während der Theil
G lediglich die Ausgleichung des Gewichtes des auf
einer Unterlagsschiene u schleifenden Theiles T zum Zwecke hat. Mit L
ist eine um das Halslager H drehbare Schiene
bezeichnet, die zu beiden Seiten des Verticalzapfens V
mit einem Schlitze versehen ist. In den Schlitz unter dem Segmente S greift eine Warze w,
welche sich senkrecht unterhalb des Theilrisses der Zahnschiene ZZ an letzterer selbst befindet. Die Zahnschiene ZZ ist mittels einer Hülse M auf eine Gleitstange A gesteckt und
verschiebt sich auf ihr, sobald die Schiene L gedreht
wird. Das Verschieben der Zahnschiene hat die Drehung des Segmentes S, des mit ihm fest verbundenen Verticalzapfens V und der Schiene T zur
Folge, und zwar dreht sich letztere in demselben Sinne wie die Schiene LL. Während dieser Drehungen reist der Stift oder die
Nadel b, von der Schiene L
geradlinig in dem Schlitze einer Querschiene Q geführt,
auf der Tafel t einen Kreisevolventbogen mn an.
Die Richtigkeit dieser Behauptung läſst sich leicht nachweisen.
Nach einer Drehung der Schiene L um den Winkel φ aus ihrer Anfangslage, wird, wenn r der Theilkreishalbmesser des Segmentes S ist, die Zahnstange geradlinig um r\ tg\
\varphi verschoben, wobei sich gleichzeitig auch das Segment S um einen Winkel ψ
verdreht, dessen Gröſse sich aus der Gleichung r\psi=r\ tg\
\varphi ergibt. War nun der Stift b in
der Schiene L anfänglich auf die Entfernung R vom Mittelpunkte des Zapfens V eingestellt, so ist er, nach vollführter Drehung der Schiene L um den Winkel φ, vom
Mittelpunkte O des Zapfens V um die Strecke \varrho=R\sqrt{1+tg^2\varphi}
entfernt. Der Winkel Δ (Fig. 1), um welchen die
Mittellinie der Schiene T von der Mittellinie der
Schiene L nach einer Drehung um den Winkel φ absteht, ist \Delta=\psi-\varphi
und demnach
tg\ \Delta=\frac{tg\ \psi-tg\ \varphi}{1+tg\
\varphi\ tg\ \psi}.
Nachdem nun, wie oben angeführt, r\ tg\
\varphi=r\psi ist, so ist auch
\varrho=R\sqrt{1+\psi^2} und tg\ \Delta=\frac{tg\
\psi-\psi}{1+\psi\ tg\ \psi}, welche zwei Ausdrücke mit der bekannten
Polargleichung einer zum Halbmesser R gehörigen
Kreisevolvente übereinstimmen. Zu Anfang der Drehung wird, da für kleine Winkel
Tangente und Bogen nur unbedeutend von einander abweichen, die Schiene T mit der Schiene L
ziemlich gleichen Schritt halten; mit dem Fortschreiten der Drehung aber überholt
die Schiene T die Schiene L mehr und mehr.
Die Querschiene Q läſst sich an zwei
Führungsstangen B1, die
Tafel t an der verticalen Rippe der Schiene T verschieben und unter den Stift b bringen. Entspricht nun R dem Halbmesser des Grundkreises eines Zahnrades, so entspricht der
Evolventenbogen mn der Zahnflanke. Behufs Anfertigung
einer Lehre für die Zahnflankenkrümmung befestigt man auf der Tafel t ein Stück Blech, nachdem auf demselben auſser dem
Grund- und dem Theilkreise auch die Richtung eines Halbmessers angerissen wurde, um
das Blech auf der Tafel richtig einstellen zu können.
V. Thallmayer.
Tafeln