| Titel: | L. Abbot's Ellipsograph. |
| Fundstelle: | Band 255, Jahrgang 1885, S. 20 |
| Download: | XML |
L. Abbot's Ellipsograph.
Mit Abbildungen auf Tafel
2.
L. Abbot's Ellipsograph.
Der von Levi Abbot in Cambridge, Mass., Nordamerika (*
D. R. P. Kl. 42 Nr. 28638 vom 1. April 1884) angegebene Eilipsograph zeichnet sich
dadurch vortheilhaft aus, daſs das ganze Instrument seitwärts von der Stelle, wo die
Ellipse zu zeichnen ist, auf die Zeichnenfläche aufgesetzt wird. Die Ellipse wird
dabei in der Weise gezogen, daſs der Schreibstift gleichzeitig zwei zu einander
senkrechte Sinusversusbewegungen macht.
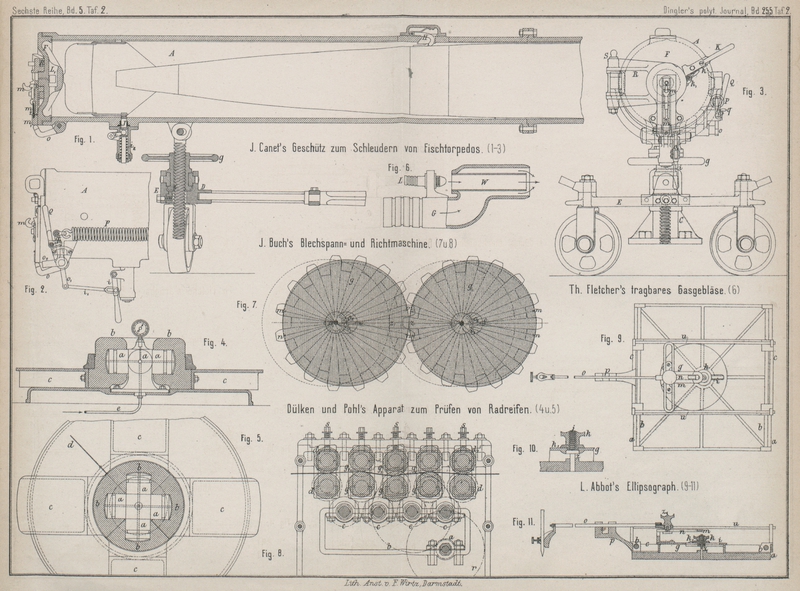
Hiernach ist die Anordnung des Instrumentes leicht zu verstehen. Wie aus Fig. 9 und 11 Taf. 2
hervorgeht, ist der Schreibstift in dem Arme des Schlittens o befestigt. Dieser Schlitten o wird in der
Führung p und auf den Stangen u des Rahmens c geführt und durch den in die
Schleife des Schlittens o greifenden Kurbelzapfen z1, welcher im Kreise
um den Zapfen z herumgeführt wird, verschoben. Der
Rahmen c ist seinerseits rechtwinklig zu o auf den Stangen b der
Grundplatte a verschiebbar und wird durch die runde
Scheibe g hin- und hergeführt, welche gleichzeitig mit
dem Zapfen z1 um den
Zapfen z gedreht wird. Um die Gröſse der Verschiebungen
des Schlittens o sowohl, als auch des Rahmens c zu verändern, kann einestheils die Excentricität der
Scheibe g, andererseits die des Zapfens z1 gröſser oder
geringer gemacht werden. Zu dem Zwecke läſst sich der Zapfen z an jeder Stelle des Schlitzes i in der
Scheibe g feststellen, indem derselbe die aus Fig. 10 Taf. 2
ersichtliche Anordnung besitzt. Ueber den Zapfen z ist
die auſsen mit Schraubengewinde versehene Hülse j
geschoben, welche mit einem vierkantigen Kopfe in dem Schlitze der Scheibe g liegt und so gegen jede Drehung geschützt ist. Ueber
derselben liegt die Unterlegescheibe k1, welche durch die geränderte Mutter k fest auf die Scheibe g gepreſst werden
kann, womit die radiale Verschiebung der letzteren aufgehoben ist, ohne daſs die
freie Drehbarkeit um den Zapfen z gestört wird. Ebenso
kann der Zapfen z1
durch Anziehen seiner geränderten Mutter an jeder Stelle des Schlitzes n in dem mit der Scheibe g
fest verbundenen Arme m festgeklemmt werden, wobei
seine Verschieblichkeit in der Schlitzführung des Schreibstiftschlittens o unbeeinfluſst bleibt. Es ist nun klar, daſs bei der
mittels des Zapfens zl
bewirkten Drehung der Scheibe g jeder Punkt des
Schlittens o, folglich auch der Schreibstift eine
Ellipse beschreiben wird, deren Achsen Verhältnisse durch die von der Einstellung
der Zapfen z und z1 abhängigen Excentricitäten des letzteren und der
Scheibe g bedingt sind. Selbstverständlich können die
beiden Achsen der Ellipse auch gleich sein, dieselbe kann also auch in einen Kreis
übergehen.
Tafeln