| Titel: | Ueber Versuche zur Klarstellung des Wirkungsgrades des Locomotivkessels; von Prof. H. Gollner in Prag. |
| Autor: | H. Gollner |
| Fundstelle: | Band 268, Jahrgang 1888, S. 540 |
| Download: | XML |
Ueber Versuche zur Klarstellung des
Wirkungsgrades des Locomotivkessels; von Prof. H. Gollner in Prag.
(Schluſs des Berichtes S. 494 d. Bd.)
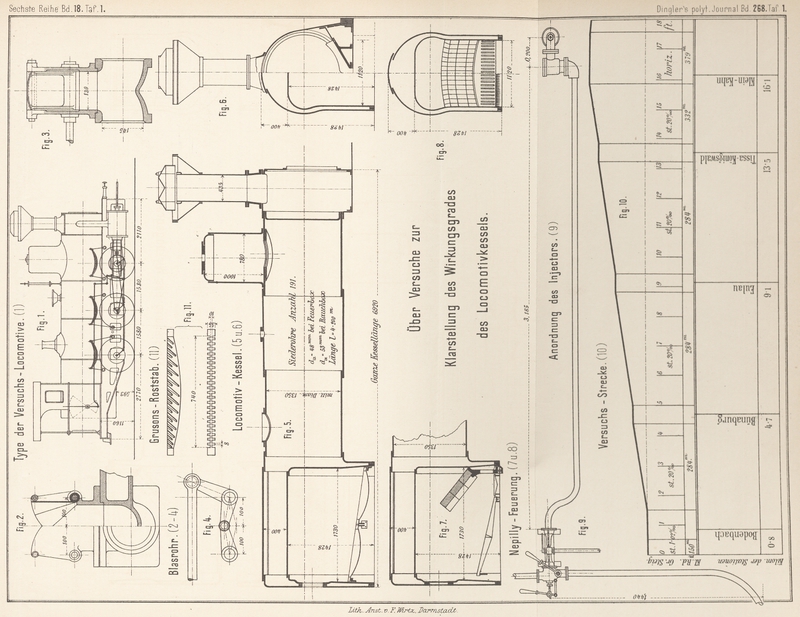
Mit Abbildungen auf Tafel
1 und 2.
Gollner, Klarstellung des Wirkungsgrades des
Locomotivkessels.
Die Beziehungen zwischen der specifischen Dampfnässe (x)
und dem Strahlungsverluste (W7
) bezieh. dem Werthe (Ks), sowie der erreichten Verdampfungsziffer
(Mn : B) lassen
sich in folgender Weise sicherstellen:
Bezeichnet man die Summe der Wärmeverluste (W1 bis + W6) + (W9 + W10
) mit ΣW und wird die
Gröſse H – ΣW = ΔW gesetzt, so ist
ΔW – (W7 + W8
) die von 1k
Brennstoff gelieferte Nutzwärme, welche sich wieder ausdrückt durch
\frac{M_n}{B}\,(1-x)\,(\lambda-q_0)
, wobei (Mn die producirte Gewichtsmenge Dampf von
der specifischen Nässe = x bedeutet, und wobei Mt = Mn(1 – x) die
unter gleichen Umständen erzeugte Gewichtsmenge trockenen Dampfes ausdrückt. Die mit
Benutzung der Werthe W7
und W8 dargestellte
Beziehung:
\Delta\,W-\left(\frac{O}{B}.K_s.T_b.\Delta+\frac{M_n}{B}.x.q_w\right)=\frac{M_n}{B}.(1-x)\,(\lambda-q_0)
kann nach mehrfachen Umwandlungen ausgedrückt werden
durch:
x=\frac{M_n\,(\lambda-q_0)-B\,\Delta\,W}{M_n\,[\lambda-(q_w+q_0)]}+\frac{O.T_b.\Delta}{M_n\,[\lambda-(q_w+q_0)]}\,K_s.
Diese Gleichung entspricht der allgemeinen Form x = A +
C . Ks als
Gleichung einer Geraden in specieller Lage gegen das Coordinatensystem, welche aus
den Diagrammen Fig.
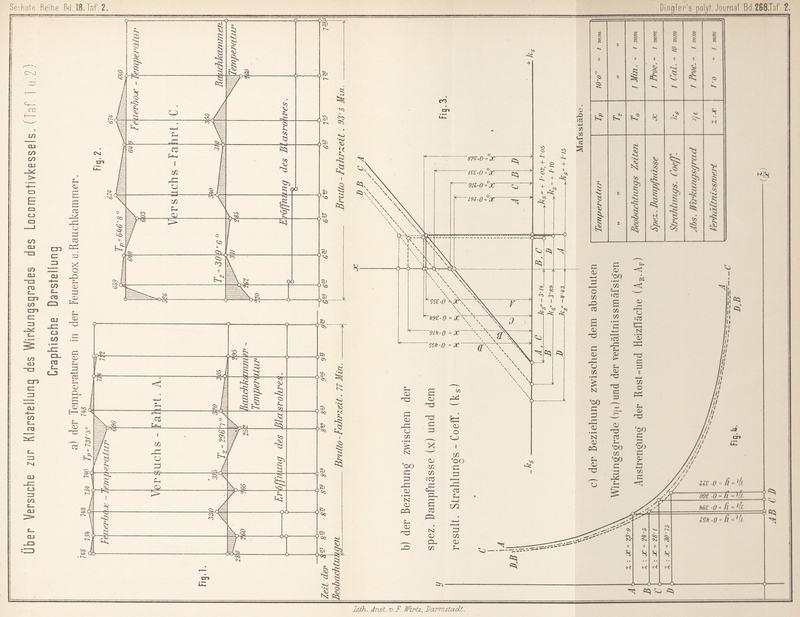
3 Taf. 2 zu ersehen ist. Die entwickelte Gleichung kann auch geschrieben
werden:
XVII)
x=\frac{O.T_b.\Delta}{M_n[\lambda-(q_w+q_0)]}.K_s+\frac{(\lambda-q_0)-\left(\frac{B}{M_n}\right)\,\Delta\,W}{\lambda-(q_w+q_0)};
sie laſst erkennen, daſs sich die specifische Dampfnässe aus 2
Theilen additionell zusammensetzt, von welchen die Gröſse des ersten Theiles von den
Strahlungsverhältnissen der Kesseloberfläche (W7
) abhängig ist, während der zweite und im Allgemeinen
wesentlich gröſsere Theil eine Function des
Betriebes bezieh. des Wirkungsgrades (ηt) der ganzen Kesselanlage ist. Zur Verminderung der Dampfnässe für den Locomotivkessel
führt:
a) eine geringe wärmedicht gehaltene Kesseloberfläche
O, welche einer hohen Lufttemperatur (t) ausgesetzt ist, wobei die Bruttofahrzeit möglichst
nahe der Nettofahrzeit Tn kommen soll;
b) ein hoher Wirkungsgrad der Kesselanlage ηt selbst, d.i. wegen ΔW groſs, H – ΣW groſs und
ΣW klein, daher (B :
Mn) klein, d.i. (Mn : B) groſs, nämlich
möglichste Schonung der Kesselanlage durch Einleitung einer geringen Anstrengung (AF und AR) der Heiz- und
Rostfläche zur Erreichung einer hohen Verdampfungsziffer (Mn : B).
Für den Locomotivkessel können die eben angeführten Bedingungen nicht erfüllt
werden. Zunächst ist es nicht möglich, den Werth Ks Cal. besonders günstig zu stellen, da nur
eine Metallverschalung der Kessel unter Anwendung einer stagnirenden Luftschichte
zwischen dieser und der Kesselwandung (oder noch unter Verwendung einer Filzlage,
dichte Leinwand) zulässig erscheint, weiter sind die Werthe Tb und t
von äuſseren, vielfach sehr ungünstig wirkenden Verhältnissen, die keine Abänderung
zulassen, abhängig. Im Allgemeinen stellt sich die absolute Gröſse Oqm oder der
Verhältniſswerth O : Mn nicht sehr unvortheilhaft, hingegen
werden diese günstigen Einflüsse von den mehrfachen durchaus schädlichen
Einwirkungen der übrigen maſsgebenden Gröſsen wesentlich eingeschränkt.
Im Weiteren ist zu berücksichtigen, daſs im Allgemeinen ein hoher Wirkungsgrad ηt des Locomotivkessels
wegen der unvermeidlichen Forcirung seiner Heiz- und Rostfläche nicht zu erzielen
ist, in Folge dessen gleichfalls ein höherer Werth (x)
für die specifische Dampfnässe in Aussicht zu nehmen sein wird. Aus obiger Gleichung
geht weiter hervor, daſs die specifische Dampfnässe x
für Ks = O, d.i. unter der Voraussetzung, daſs keine schädliche
Strahlung nach auſsen stattfände, den kleinsten möglichen Werth, d.i.
x\
\mbox{min.}=\frac{(\lambda-q_0)-\left(\frac{B}{M_n}\right)\,\Delta\,W}{[\lambda-(q_w+q_0)]}
erreicht; die specifische Dampfnässe x wird = O für
K_s=-\frac{M_n\,(\lambda-q_0)-B\,\Delta.W}{O.T_b.(w-t)}
d.h. wenn der Strahlungscoefficient Ks den Charakter eines
Wärmedurchgangscoefficienten von Luft gegen das Kesselinnere annimmt, also wenn der
Kesseloberfläche von auſsen Wärme zugeführt werden würde.
Aus den eben gelieferten Darstellungen geht endlich hervor, daſs die Erzeugung von trockenem
Kesseldampf bei Locomotiven unmöglich ist, daſs bei stationären Dampfkesselanlagen
hingegen unter dem Einflüsse des erhitzten Mauerwerkes, wenigstens zweitweise, + Ks in – Ks übergehen kann,
wodurch der Werth x sehr nahe oder gleich Null würde,
wenn eben die übrigen schon früher hervorgehobenen Bedingungen erfüllbar sind und
auch effectiv erfüllt werden.
Der Locomotivkessel ist hiernach trotz seiner günstig angeordneten inneren Heizfläche
betreffend die Wärmeverluste durch Strahlung und in Folge Dampfnässe im Nachtheile
gegenüber den gut eingemauerten stationären Dampfkesseln, wie auch die für die vier
Versuchsfahrten A bis D berechneten Werthe von x
nachweisen; die zu Berechnung von W8 und des folgenden Correctionsfactors ξn nöthigen
Hilfsgröſsen sind in der Tabelle XIX zusammengestellt.
Tabelle XIX.
Art der Feuerung
Nepilly-Feuerung
Gewöhnliche Plan-feuerung
Zeichen der Versuchsfahrt
A
B
C
D
Hilfs-Gröſsen
O . Tb . Ks . ΔMn[λ – (qw + q0)]Mn(λ – q0
)ΣWΔWB . ΔW
188121,02192755,93355149,61841,52527,52767612,5
205520,72396201,73357705,02351,32504,72562308,1
243805,62782082,53853946,52447,52033,53086853,0
200718,02419057,23362977,22575,71960,32969978,0
Minimale specifische Dampfnässe
x
0,267
0,331
0,276
0,368
Effective specifische Dampfnässe
x
0,355
0,416
0,364
0,451
Gewichtsmenge trocke- ner Dampf
Mt = Mn(I – x)
3339,6
3043,5
3787,3
2879,0
Verhältniſswerth
Mt : Mt
1,14
1,18
1,14
1,20
Gewichtsmenge trockenen Dam- pfes für
kmt 1''
Bruttofahrz.Nettofahrz.
0,0002160,00024
0,0001910,00023
0,0001980,00024
0,0001790,00023
Resultirender Strah- lungscoefficient
Ks Cal.
+ 1,15
+ 1,02
+ 1,05
+ 1,10
Der Wärmeverlust W8
berechnet sich schlieſslich nach Kenntniſs des Werthes x wie folgt:
XVIII) W_8=\frac{x.M_n.q}{B} und XIX)
\xi_n=\left(1-\frac{x.M_n.q^w}{H}\right)
Beurtheilt man zunächst die gefundenen Näherungswerthe für xmin, welche für die Verwendung der
Nepilly-Feuerung zwischen 26,7 und 33,1 Proc., für
die Planfeuerung zwischen 27,6 und 36,8 Proc. liegen, und berücksichtigt, daſs diese
Werthe unter der Voraussetzung Geltung haben, daſs der Strahlungsverlust W7 = O sei, so muſs erkannt werden, daſs die im günstigsten
Falle resultirende specifische Dampfnässe allerdings an sich eine sehr beträchtliche
ist und sich der günstige Einfluſs der Nepilly-Feuerung
gegenüber der gewöhnlichen Planfeuerung nur in sehr bescheidenem Maſse zur Geltung
bringt. Die oben angegebenen specifischen Werthe lassen erkennen, daſs die
Strahlungsverhältnisse für den Locomotivkessel trotz der Innenfeuerung und der
Innenfeuerzüge sehr ungünstige sind und jene für gut eingemauerte Dampfkessel, für
welche durchschnittlich ein Strahlungsverlust von 8 Proc. (Einzelkessel), von 15
Proc. (Batteriekessel) resultirt, weit übersteigen.
Die gefundene effective specifische Dampfnässe im Werthe von 35,5 bis 41,6 Proc. für
Nepilly- und von 36,4 bis 45,1 Proc. für die
gewöhnliche Planfeuerung, je nachdem Nuſs- oder Mittelkohle verfeuert wurde, muſs
als sehr bedeutend erkannt werden. Die für alle vier Versuchsfahrten stattgehabte
lebhafte Forcirung der Heiz- und Rostfläche, der geringe Werth der ermittelten
Verdampfungsziffer weisen schon auf hohe Näherungswerthe hin. Zieht man in Betracht,
daſs ein stationärer Röhrenkessel von folgenden Hauptverhältnissen und zwar Ft : R = 48,75, Mn : Ft = A = 10,2,
B : R = AR = 75 (für Unterfeuerung) Dampf von der
specifischen Nässe x = 16,5 Proc. liefert, so finden
die für die effectiven Betriebsverhältnisse des Locomotivkessels für die vier
Versuchsfahrten ermittelten Werthe der specifischen Dampfnässe ihre völlige
Erklärung und Begründung.
Der Wärmeverlust in Folge der Dampfnässe W8 ist gleichfalls ein bedeutender und erreicht etwa
7,0 Proc.
Nachdem es – wie ersichtlich – auf dem Rechnungswege nur möglich ist, einen
Näherungswerth für die Gröſsen x und W8 zu finden, nachdem
der Wärmedurchgangscoefficient Ks von Fall zu Fall auch nur annähernd ermittelt werden kann und
die Kenntniſs des Werthes x aus mehrfachen Gründen von
Wichtigkeit ist, so liegt das dringende Bedürfniſs vor, auf dem Wege des Versuches
durch ein möglichst direktes Verfahren den Werth von x
sicher zu stellen und die bisher versuchsweise angewendeten Methoden zur Bestimmung
desselben Werthes noch weiter auszubilden und derart zu vervollkommnen, daſs die
hier berührte Frage auch unter den für den Betrieb des Locomotivkessels maſsgebenden
extremen Verhältnissen befriedigend gelöst werden kann- bis dahin werden die
Resultate der analytischen Methode genügen müssen.
W9, Wärmeverlust in Folge Anwendung des Injectors für die
Zuführung des Speisewassers in den Kessel. Dieser Verlust besteht a) aus einem
gewissen Abkühlungsverluste und b) aus dem Wärmeconsum in Folge der Verrichtung
einer gewissen mechanischen Arbeit seitens des Kesseldampfes. Nach direkten
Messungen anläſslich der Specialuntersuchungen des angewendeten Injectors Nr. 7 nach
System Anschütz-Schlu wurden für die gegebenen
mittleren Temperaturen (t0 ... q0) des
Tenderwassers jene Wassertemperaturen (ti ... qi) ermittelt, welche für die
Eintrittsstelle desselben in den Kessel sich ergeben, wenn gewisse Dampfspannungen
(pKat) bestehen. Nachdem die dem Kessel zugeführte
Wassermenge (Q0k), welche sowohl als Speisewasser wie als
Einspritzwasser für die Rauchkammer während der Versuchsfahrten (Bergfahrten) zur Verwendung kam,
bestimmt werden konnte, so berechnet sich die durch den Injector consumirte
Dampfmenge (Mik), deren Gesammtwärme für lk (λ – q0) Cal. beträgt, nach der Beziehung:
Mi(λ –
q0) + Q0q0 = (Mi + Q0
)qi oder
\frac{Q_0}{M_i}=v=\frac{(\lambda-q_0)-q_i}{q_i-q_0};\
M_i=\frac{Q_0}{v}
Hierbei hat qi die
Bedeutung der effectiven Flüssigkeitswärme des in den Kessel tretenden Wassers,
dessen Temperatur ti
eben durch die oben erwähnten Versuche direkt ermittelt wurde, daher auch Mi die effective vom Injector benöthigte Dampf menge
bezeichnet, welche zur Förderung von Q0k Kesselwasser
diente. Berücksichtigt man, daſs der Wärmeaufwand zur Erzeugung von Q0k Wasser von der Temperatur ti aus Wasser von der
Temperatur t0 : Q0
(qi – q0) beträgt, ferner, daſs in Folge der Anwendung des
Injectors mit Rücksicht auf die (Fig. 9 Taf. 1) gegebene
Disposition und Dimensionirung desselben Mik Dampf,
also eine Wärmemenge von Mi
(λ – q0) Cal. zu gleichem Zwecke erfordert
werden, so ergibt sich zunächst Mehraufwand an Wärme von:
W_i=\left[\frac{M_i\,(\lambda-q_0)-Q_0\,(q_i-q_0)}{B}\right].
Nachdem für den vorliegenden Fall der Wärmeverbrauch Wa in Folge Verrichtung einer bestimmten
mechanischen Arbeit und zwar durch Einpressen der Wassermenge Q0k in den Kessel von der Spannung pkat in der Zeit Tb (Minuten)
W_a=\frac{(h+h_s)\,Q_0}{424.B} ist, wobei die effective
Förderhöhe h = 10,0 . pkm, die
mittlere Widerstandshöhe hz
= 15m,0 erreicht, so berechnet sich W9 wie folgt:
XX)
W_9=W_i+W_a=\frac{M_i\,(\lambda-q_0)-Q_0\,\left((q_i-q_0)+\frac{h+h_s}{424}\right)}{B}
und der Correctionsfactor für den Wirkungsgrad ηt der
Kesselanlage:
XXI) \xi_J=\left(1-\frac{W_g}{H}\right).
In der folgenden Tabelle sind nun die den Verhältnissen der vier Versuchsfahrten (A
bis D) entsprechenden Werthe, welche theils im Versuchs-, theils im Rechnungswege
gefunden wurden, eingetragen, und sei insbesondere bemerkt, daſs Q0k jene Wassermenge bezeichnet, welche vom Injector
für die Bergfahrt (also exclusive des Bedarfes an Wasser für das Dampf halten
während der Thalfahrt) und zwar für die Kesselspeisung, Einspritzung in die
Rauchkammer dem Kessel zugeführt werden muſste; diese Wassermenge Q0 ist im Allgemeinen
von der effectiven Speisewassermenge Mn verschieden. Der Wärmeverlust W9 ist für die vier
Versuchsfahrten A bis D wegen des continuirlichen
Betriebes des Injectors an und für sich sehr gering und überdies
befriedigend übereinstimmend.
Tabelle XX.
Art der Feuerung
Nepilly-Feuerung
Gewöhnliche Plan-feuerung
Zeichen der Versuchsfahrt
A
B
C
D
Flüssigkeitswärme der Speise- wasser.
q0Cal.
14,0
17,7
14,2
20,1
Flüssigkeitswärme des in den Kessel ein tretenden
Wassers
qi
65,0
69,0
63,0
69,0
Effective mittlere Kesselspan- nung in at
pk
9,7
9,7
9,3
9,2
Brutto Wasser menge für 1 Bergfahrt in den
Kessel gespeist
Q
0
k
5177,7
5227,4
5989,5
5347,0
Dampfconsum seitens des Injectors
Mi
k
445,5
450,4
486,9
441,9
Verhältniſswerth v = (Q0
: Mi)
v
11,72
11,60
12.30
12,10
Förderhöhe (h + hz) in
m
112,0
112,0
108,0
107,0
W10, Wärmeverlust in Folge Einspritzens heiſsen
Kesselwassers in die Rauchkammer. Dieser Wärmeverlust war für die drei
Versuchsfahrten B, C, D unvermeidlich geworden, nachdem sich während derselben und
besonders bei der Fahrt D bedeutende Mengen glühender Rückstände aus der Verbrennung
in der Rauchkammer ansammelten und das Erglühen der Wandungen derselben zu
befürchten war.
Nachdem schon vor den entscheidenden Versuchsfahrten durch den am Anfange der
Abhandlung beschriebenen Special versuch die Leistungsfähigkeit des Einspritzhahnes
für eine Zeiteinheit und bei verschiedenen Kesselspannungen ermittelt wurde und
während der freien Fahrt auch die Zeit beobachtet wurde, während welcher der
bezeichnete Hahn bei einer bestimmten Dampfspannung eröffnet war, um das
Einspritzwasser in die Rauchkammer zu liefern, so konnte auch schlieſslich der
Wärmeverlust W10
berechnet werden, dessen Werth sich in der allgemeinen Form ausdrücken läſst:
XXII) W_{10}=\frac{q_0\,\times\,q_w}{B}
wenn q0 die Gewichtsmenge Einspritzwasser bezeichnet, welche für die
Versuchsfahrt verwendet wurde, und qw die der jeweiligen Wassertemperatur
entsprechende Flüssigkeitsmenge angibt.. Der aus W10 sich ergebende Correctionsfactor W10 berechnet sich wie
folgt:
XXIII)
\xi_{10}=\left(1-\frac{q_0.q_w}{H}\right)
Die Ergebnisse der zum Zwecke der Bestimmung von W10 durchgeführten Beobachtungen sind in der
folgenden Tabelle XXI zusammengestellt. Aus denselben geht hervor, daſs die Dauer
der bezeichneten Einspritzperiode für die einzelnen Fahrten sehr verschieden
ausfielen und zwischen 0 und 170 Secunden variirten. Die Verhältnisse während der
Fahrt D erforderten die gröſste Einspritzwassermenge, überhaupt zeigte sich in
dieser Richtung die gewöhnliche Planfeuerung wesentlich ungünstiger als die Nepilly-Feuerung, welche im Stande war, die
Auswurfmengen zu reduciren.
Tabelle XXI.
Art der Feuerung
Nepilly-Feuerung
Gewöhnliche Plan-feuerung
Zeichen der Versuchsfahrt
A
B
C
D
Zeitdauer des Einspritzens
te''
0,0
19,0
56,0
170
Eingespritzte Wassermenge
q
0
k
0,0
16,0
34,7
103,0
Mittlere effective Kesselspan- nung
p
k
at
9,7
9,7
9,3
9,2
Flüssigkeitswärme
qwCal.
184,5
184,5
180,0
180,0
Auf Grund des bisher vorgeführten Versuchs- und Rechnungsmateriales ist es nunmehr
möglich, die besonderen Werthe der bisher allgemein dargestellten Wärme Verluste für
1k Brennmaterial für die Versuchsfahrten A bis
D zu bestimmen und dieselben sowohl den absoluten Gröſsen nach in Calorien, als auch
in Procenten des theoretischen Heizwerthes (H) des
bezüglichen Brennmaterials auszudrücken, um die nöthige Uebersicht über die absolute
und relative Gröſse der Verlustwerthe zu gewinnen.
Die Haupt-Tabelle XXII bietet in dieser Beziehung den vollständigen Ueberblick und
enthält gleichzeitig die nöthigen Angaben über den Träger, sowie über die Art der
verlorenen Wärme für 1k Brennmaterial; die
einzelnen Wärmeverluste W1 bis einschlieſslich W10 sind derart in zwei Gruppen zusammengefaſst, daſs
sofort der Einfluſs der Anordnung und Anstrengung der Feuerung und der Beizfläche auf die Gröſse
der bezüglichen Verlustwerthe erkannt werden kann; die Wärmeverluste W9 und W10 als ganz specielle
Werthe sind in eine dritte Gruppe vereinigt. Endlich ist noch der summarische Werth
ΣW der zehn Wärmeverluste, sowie die resultirende
Nutzwärme Wn für 1k Brennmaterial ermittelt und in die Tabelle
eingetragen, um derart die für die folgende Bestimmung des absoluten Wirkungsgrades
des Locomotivkessels maſsgebenden Gröſsen sofort überblicken zu lassen.
Aus den in die Tabelle XXII zusammengestellten Schluſsergebnissen lassen sich bei
Beachtung ihrer absoluten und procentischen Werthe folgende Schlüsse ziehen:
1) Die Wärmeverluste in Folge Betriebes des Loeomotivkessels, welche durch die
„unentwickelte“ Wärme in den Verbrennungsrückständen entstehen (W1, W2, W3
) sind mit Rücksicht auf die Natur und das Format der
verfeuerten Brennmaterialien von geringerer Bedeutung; bei Verwendung der
gewöhnlichen Planfeuerung erreichen dieselben für Nuſskohle und Mittelkohle 3,1 bis
3,8 Proc., für die Nepilly-Feuerung bei denselben
Brennmaterialien 1,7 bis 1,6 Proc., also etwa die Hälfte der ersteren Werthe;
hieraus geht hervor, daſs die letztere Feuerung als Halbgas-Feuerung unter übrigens
gleichen Umständen eine vollkommenere
Haupt-Tabelle XXII.
Art der Feuerung
Nepilly-Feuerung
Gewöhnliche Planfeuerung
Zeichen der Versuchsfahrt
A
B
C
D
P.-Nr.
Wärmeverluste für1k Brennmaterialin Folge
Be-zeich-nung
Träger der verlorenenWärme
Art derverlorenenWärme
inCalorien
inProcentenvon H
inCalorien
inProcentenvon H
inCalorien
inProcentenvon H
inCalorien
inProcentenvon H
1
W
1
Rückstände im Aschen-kasten
Unentwickelt
27,9
0,64
47,2
0,97
60,5
1,35
74,0
1,64
2
W
2
Rückstände in derFeuerbox
„
8,8
0,21
11,7
0,25
7,6
0,17
6,2
0,14
3
Anordnung
undAnstrengungderFeuerungsanlage
W
3
Rückstände in derRauchkammer
„
75,7
1,73
77,3
1,59
139,3
3,12
173,8
3,83
4
W
4
Auswurf, Rauch
Unentwickeltund entführt
1054,8
24,12
1558,2
32,09
1427,6
31,84
1622,7
35,7
5
W
5
Kohlenoxydgas
Unentwickeltund entführt
18,7
0,43
0,0
0,0
88,9
1,98
80,9
1,78
6
W
6
Entweichende Rauchgase
Entführt
703,2
16,09
630,0
12,97
700,0
15,62
585,0
12,89
7
Anordnung undAnstrengungder
Heizfläche
W
7
Kessel-Oberfläche
Verloren
171,8
3,94
200,9
4,13
201,1
4,49
159,3
3,51
8
W
8
Wasserdampf
Entführt
309,8
7,09
390,9
8,05
257,0
5,73
337,9
7,45
9
Anwendungdes Injectors
W
9
Injector
Verloren
23,6
0,55
24,2
0,51
16,0
0,36
18,4
0,41
10
Einspritzen desKesselwassers indie
Rauchkammer
W
10
Kesselwasser
Verloren
0,0
0,00
2,7
0,05
7,6
0,18
14,7
0,32
ΣW
Summe der Wärmeverluste für 1k Brennmaterial
Verloren
2394,3
54,80
2943,1
60,61
2905,6
64,84
3072,9
67,74
Wn
Nutzwärme für 1k Brennmaterial
Nutzbar
1974,7
45,20
1912,9
39,39
1575,4
35,16
1463,1
32,26
Verbrennung zu liefern vermag als die gewöhnliche
Planfeuerung.
2) Der gleichfalls für die Charakteristik der ausgenutzten Feuerung wesentliche
Wärmeverlust (W5) in
Folge Bildung brennbarer Rauchgase ist gleichfalls an und für sich unbedeutend,
erreicht für die gewöhnliche Planfeuerung 1,8 bis 2,0 Proc. und sinkt für die Nepilly-Feuerung bei annähernd gleichen
Brennmaterialien hinsichtlich Heizwerth und Korngröſse auf 0,4 Proc. (in einem Falle
auf 0,0 Proc.) herab. Dieses Resultat ist um so beachtenswerther, als es bei
erheblicher Forcirung der Feuerungsanlage und bei entschieden zu karg bemessener
Rostfläche der gewöhnlichen Planfeuerung erreicht wurde; dasselbe läſst gleichzeitig
auch die entscheidende Wirkung des Blaserohres erkennen. Die bisher hervorgehobenen
Wärmeverluste, welche durch die Art und Anstrengung der Feuerungsanlage bei
Verwendung von (Nuſs- und Mittel-) Braunkohle bedingt werden, erreichen für die Nepilly-Feuerung einen Gesammtwerth von 2,8 bis 3,0
Proc., für die gewöhnliche Planfeuerung einen solchen von 6,6 bis 7,4 Proc.
3) Der absolut gröſste Wärmeverlust (W4), welcher ebenfalls von der Art und dem Betriebe
der Feuerungsanlage, sowie vom Brennmaterial abhängig ist und dessen Gröſse durch
den Effect des Blaserohres bestimmt ist, ist jener, der als Wärmeverlust in Folge
„Auswurfes“ bezeichnet wurde. Die diesem entsprechende
„unentwickelte“ und „entführte“ Wärme beträgt für Nepilly-Feuerung 24 bis 32 Proc., für die zweite
Feuerungsanlage etwa 32 bis 36 Proc., für die gleichen Brennmaterialien bedingt die
erstere Feuerungsanlage ein Sinken dieses Verlustes um etwa 8 Proc. (Nuſskohle) und etwa 4 Proc. (Mittelkohle). hieraus kann sofort erkannt werden, daſs
a) die Nuſskohle II weniger dem „Auswurf“ unterliegt, als die Mittelkohle I,
welche Thatsache durch die dichtere Lagerung der ersteren Kohlensorte auf dem Roste
erklärt ist-
b) daſs die Nepilly-Feuerung im Vergleiche zur
gewöhnlichen Planteuerung wegen der Fähigkeit, zur Verminderung des
„Auswurfes“ beizutragen, als eine ökonomische Anlage bezeichnet werden
muſs. Zur effectiven Herabsetzung dieses Wärmeverlustes sind die schon an früherer
Stelle gekennzeichneten Mittel um so vollständiger und energischer in Anwendung zu
bringen und auszunutzen, als der in Rede stehende Wärmeverlust W4 der absolut und
relativ gröſste Verlust ist und – wie erwähnt – nach den durchgeführten
Untersuchungen 24 bis 36 Proc. erreichen kann.
4) Der sogen. „Essenverlust“ (W6) erscheint auffällig reducirt und schwankt dessen
Werth zwischen etwa 13 und 16 Proc., erreicht somit beiläufig die Hälfte des
analogen Werthes für stationäre Kesselanlagen. Hinsichtlich dieses Verlustes ist der
Einfluſs der Nepilly-Feuerung gegenüber der
gewöhnlichen Planfeuerung ein verhältniſsmäſsig geringer; aus den Tabellenwerthen geht
übrigens hervor, daſs sich W6 für die Verfeuerung von Nuſskohle etwas günstiger als für Verwerthung
von Mittelkohle entwickelt. Der für die vier Versuchsfahrten A bis D berechnete
Essenverlust ist bezieh. etwa 0,66, 0,40, 0,5 und 0,36 des Verlustes in Folge
„Auswurfes“. Nach den vorangegangenen Darstellungen betreffend die
Ursachen des „Essenverlustes“ ist zu erkennen, daſs derselbe im Gegensatze
zum „Auswurfverluste“ kaum noch mehr reducirt werden kann.
5) Die neben W6 von der
Anstrengung der Gesammtheizfläche abhängigen Wärmeverluste W7 und W8, welch letztere Werthe, wie schon an früherer
Stelle begründet, als Näherungswerthe aufzufassen sind, zeigen verhältniſsmäſsig
geringe Unterschiede hinsichtlich ihrer Gröſse; insbesondere ist der
Strahlungsverlust W7
für die vier Versuchsfahrten von befriedigender Uebereinstimmung und ergeben die
Grenzwerthe etwa 3,5 und 4,5 Proc; der procentische Verlust in Folge Dampfnässe (W8) schwankt zwischen
5,7 und 8,0 Proc. und muſs als sehr bedeutend erkannt werden; die zur Verminderung
dieser Verluste an früherer Stelle angegebenen Mittel können mit Rücksicht auf
andere für die Locomotive im Allgemeinen und für die Locomotivkessel insbesondere
maſsgebenden äuſseren Verhältnisse nicht mit entscheidendem Einflüsse angewendet
werden.
6) Die Verluste W9
(Injectorverlust), W10
(Einspritzverlust) sind von sehr geringer Bedeutung an sich und gegen die früher
hervorgehobenen Hauptverluste, zu welchen W4, W6 und W8 zu zählen sind.
Aus dem eben Dargestellten geht hervor, daſs a) für den Locomotivkessel überhaupt
sehr zahlreiche Wärmeverluste bestehen und daſs b) einige derselben sich in solcher
Gröſse unvermeidlich entwickeln, daſs ein günstiger Werth des absoluten
Wirkungsgrades derselben nicht vorausgesehen werden
kann. Die lebhafte Anstrengung der Rost- und Heizfläche wegen der unvermeidlich
knappen Bemessung ihrer wirksamen Gröſsen, der gleichfalls nothwendige künstliche
Luftzug zur Führung des Feuers, ferner die ebenso unvermeidlichen wie zahlreichen
auf Abkühlung der Kesseloberfläche einwirkenden äuſseren Umstände, endlich der
periodische Betrieb desselben bei schwankender Dampfproduction und Dampfabnahme sind
die hauptsächlichsten Ursachen des geringen ökonomischen Effectes des
Locomotivkessels an sich und in Beziehung zu den stationären Dampfkesseln.
Behufs schlieſslicher Berechnung des absoluten Wirkungsgrades
ηt für den Beharrungszustand während
der „freien“ Fahrt sind die schon durch Gleichung I) ausgedrückten
Regeln zu verwerthen. Nach diesen ist zunächst:
\eta_t=\left(1-\frac{\Sigma\,W}{H}\right)=\frac{W_n}{H}=\frac{V_p}{V_t}=\frac{M_t\,(\lambda-q_0)}{B.H}=\left(\frac{A_F}{A_R}\right).\left(\frac{F}{R}\right).\left(\frac{\lambda-q_0}{H}\right).
Die erste und zweite Gleichung dieser Gruppe kann mit Benutzung der in der Tabelle XXII
zusammengestellten Werthe sofort aufgelöst werden und sind die bezüglichen
Ergebnisse in der Tabelle XXIII eingetragen. Zur Controle der erlangten Werthe wird
die dritte, vierte oder fünfte Gleichung derselben Gruppe ausgenutzt, deren
Ergebniſs bei entsprechender Durchführung der vorbereitenden und entscheidenden
Versuche mit jenem der ersten oder zweiten Gleichung übereinstimmen muſs, nachdem:
a) die sämmtlichen Wärmeverluste W1 bis W10 für den Beharrungszustand während der freien Fahrt bestimmt wurden, b) in der dritten und
vierten Gleichung die Gröſsen Mt und B jene Gewichtsmengen
trockenen Dampfes und Brennmateriales bezeichnen, welche gleichzeitig während der
angegebenen Bruttofahrzeit Tb producirt bezieh., consumirt wurden, also derart auf den zu
berechnenden Werth ηt
keinen einseitigen Einfluſs nehmen. Es ist wichtig, besonders hervorzuheben, daſs
die aus den eben vorgeführten fünf Gleichungen (von denen übrigens die erste und
zweite, sowie die dritte, vierte und fünfte Gleichung identisch sind) berechneten
Werthe von ηt aus den
eben angegebenen Gründen von jenen Störungen des Werthes des absoluten
Wirkungsgrades völlig unabhängig sind, welche durch die Fahrtunterbrechungen in den
auf der Versuchsstrecke Bodenbach-Kleinkahn disponirten Stationen unvermeidlich
hervorgerufen werden müssen.
Die dritte Gleichung ηt
= Vp : Vt liefert ein wesentliches Resultat, d.i.
Vp = Vt . ηt nämlich die wahre
praktische Verdampfungsziffer: Vp, reducirt auf trockenen
gesättigten Wasserdampf; dieser Werth allein ist maſsgebend für die Beurtheilung der
Leistungsfähigkeit des verfeuerten Brennmateriales
für die Betriebsperiode des Locomotivkessels, kann aber bei gewöhnlichen
Verdampfungsversuchen wegen Unkenntniſs der spezifischen Dampfnässe (x) nicht ermittelt werden; für denselben wird
allgemein angenommen
V_p=M_n\,:\,B=\left(\frac{M_t}{1-x}\right)\,:\,B, welcher
Werth aber entschieden zu günstig ist (s. früher Mt' : B).
Die fünfte Gleichung enthält die Gröſsenverhältnisse der Heiz- und Rostfläche, sowie
deren Anstrengung; die Gröſse
\left(\frac{F_t}{R}.\frac{\lambda-q_0}{H}\right) ist für die
Versuchsfahrten als gegeben zu betrachten und kann als Constante gleich a gesetzt werden. Der Werth ηt = y ist dann von den Urvariablen
AF = x und AR = Z abhängig. Obige
Gleichung geht nach früher über in:
y.\left(\frac{Z}{x}\right)=a.
Sie läſst den Einfluſs der Aenderungen von AF und AR auf ηt bei gegebenem Werthe
a erkennen; das Aenderungsgesetz entspricht der
gleichseitigen Hyperbel, welche für die vier Versuchsfahrten mit Rücksichtnahme auf
die dieselbe charakterisirenden Werthe auf Taf. 2 Fig. 4 verzeichnet sind.
Letztere Werthe sind übrigens auch in die Tabelle XXIII aufgenommen.
Tabelle XXIII.
Art der Feuerung
Nepilly-Feuerung
Gewöhnliche Plan-feuerung
Zeichen der Versuchsfahrt
A
B
C
D
AbsoluterWirkungsgradηt
\frac{1-\Sigma\,W}{H}=\frac{W_n}{H}
\frac{V_p}{V_t}=\frac{M_t\,(\lambda-q_0)}{B.H}
\left(\frac{A_F}{A_R}\right).\left(\frac{F_t}{R}\right).\left(\frac{\lambda-q_0}{H}\right)
0,452
0,452
0,452
0,394
0,395
0,394
0,359
0,360
0,360
0,322
0,323
0,322
Verhältniſs-werthe
AF = Mt : FtAR = B : RFt : R(λ – q0)a=\left(\frac{F_t}{R}\right).\left(\frac{\lambda-q_0}{H}\right)
18,59444,672,910,148310,812
15,53380,572,910,13269,667
17,34488,270,240,144410,143
15,05462,870,240,14139,925
Wahre prak-tische
Ver-dampfungsziff.
(Mt : B)
3,04
2,97
2,48
2,28
Die bisher gefundenen Werthe von ηt, für deren Berechnung die früher hervorgehobenen Gleichungen
benutzt wurden, haben bekanntlich die mittleren Ergebnisse der für die Dauer des
Beharrungszustandes während der „freien“ Fahrt gemachten Beobachtungen zur
Grundlage; sie stützen sich auf die Gröſsen (Mt, B, AF, AR), welche für die Bruttofahr zeit (Tb) der Probezüge, d.i.
für die Nettofahrzeit Tn mehr der Gesammtdauer der Fahrtunterbrechungen in den einzelnen
Stationen ermittelt wurden, allein wegen ihres gleichzeitig sich aufhebenden
Einflusses auf ηt für
diesen Schluſswerth nicht maſsgebend sind. Derselbe Werth η kann nun noch aus Gröſsen berechnet werden, deren Mittelwerthe, für den
Beharrungszustand während der freien Fahrt bestimmt, in
Folge des Einflusses der mehrfachen Fahrtunterbrechungen einer Correction bedürfen.
Diese Gröſsen sind a) der Wirkungsgrad des Feuerraumes ηf und b) jener der gesammten Heizfläche ηF. Die Art des
erwähnten Einflusses auf ηf ergibt sich sachgemäſs aus Folgendem. Eine Reihe von
Wärmeverlusten, und zwar W1 bis einschlieſslich W5
, deren Werthe aus Beobachtungen während des
Beharrungszustandes der „freien“ Fahrt abgeleitet wurden, ändern ihre Gröſsen
während des Stillstandes der Locomotive in den Stationen, wie schon aus der
Bedeutung von ηf = (G . c . T0
) : H hervorgeht. Dies
gilt hauptsächlich von den Wärmeverlusten W3, W4 und W5; die beiden ersteren werden z.B. für die
Stillstandsperioden gleich Null, der Verlust W5 wird in Folge Erzeugung von Kohlenoxydgas wieder
gröſser u.s.f. Alle diese Veränderungen in der Gröſse der Wärmeverluste beeinflussen
aber den Mittelwerth des effectiven Wirkungsgrades des Feuerraumes ηf, welcher nothwendig
für den Beharrungszustand der freien Fahrt einen neuen Werth annehmen muſs. Würde
ηf aus den
Beobachtungsergebnissen für den Beharrungszustand der „freien“ Fahrt berechnet werden, so müſste
ein Werth erscheinen, der für den Fall, als keine Fahrtunterbrechungen stattfinden,
richtig ist, allein für die vorliegenden vier Versuchsfahrten entschieden zu groſs
wäre. Die genaue Beziehung zwischen diesen Mittelwerthen kann allerdings nicht
festgestellt werden, nachdem Beobachtungen während der Stillstände der Locomotive in
den Stationen grundsätzlich nicht gemacht wurden, da es sich um die Ermittelung des
Werthes ηt für den
Beharrungszustand während der „freien“ Fahrt handelte; trotzdem ist aber
schon aus dem Zusammenhange der maſsgebenden Gröſsen sofort ersichtlich, daſs der
für die „freie“ Fahrt bestimmte Mittelwerth von ηf eine Veränderung erfahren muſs, deren
Gröſse sich aus dem Folgenden klar ergeben wird. Aehnliche Verhältnisse bestehen
bezüglich des Wirkungsgrades der Gesammtheizfläche ηF und der Wärmeverluste W6, W7 und W8, welche für die
zweite Hauptgröſse, d.i. den praktischen Wirkungsgrad der gesammten Heizfläche (ηF) maſsgebend sind.
Auch der effective Mittelwerth dieser Gröſse kann unter dem störenden Einflüsse der
Fahrtunterbrechungen unmöglich in Uebereinstimmung sein mit dem factisch ermittelten
Mittelwerth der Gesammtheizfläche für den Beharrungszustand der „freien“ Fahrt, wie auch schon Bedeutung von
\eta_F=\left(\frac{T_0-T_2}{T_0}\right)\,\xi hervorgeht,
nachdem sowohl T0 als
T2 für die Dauer
der Betriebsunterbrechung des Locomotivkessels wesentlich andere Werthe annehmen
müssen. Bezeichnet man den für (ηf . ηF) nach Obigem nothwendigen Correctionsfactor mit (c), so berechnet sich zunächst nach den gemachten
Beobachtungen der absolute Wirkungsgrad ηt für den Beharrungszustand der
„freien“ Fahrt ohne Rücksicht auf jene Correctur nach:
\eta_t=\eta_f.\left(\frac{T_0-T_2}{T_0}\right).\xi_s.\xi_n.\xi_J.\xi_w
oder, wenn (ξs . ξn . ξJ . ξw) = ξ
gesetzt wird, nach:
XXIV)
\eta_t=\eta_f\,\left(\frac{T_0-T_2}{T_0}\right)\,\xi.
Hierbei ist (T0 – T2
) : T0 der theoretische Wirkungsgrad der gesammten
Heizfläche und ξ der resultirende Correctionsfactor und
nöthig a) wegen des Strahlungs-, b) des Nässeverlustes, c) wegen der Verluste in
Folge der Verwendung des Injectors und des Einspritzens des Kesselwassers in die
Rauchkammer.
Der nach Gleichung XXIV berechnete Werth ηt berücksichtigt die durch die Stillstände
der Locomotive in den einzelnen Stationen hervorgerufenen calorischen Störungen,
d.i. den „Einfluſs der Fahrtunterbrechungen“ auf den absoluten Wirkungsgrad
des Locomotivkessels keineswegs, wobei noch zu bemerken
ist, daſs unter allen Umständen eben wegen der Störungen des Beharrungszustandes für
die freie Fahrt durch die „Stillstände“ der Locomotive effective
Wärmeverluste eintreten, bezieh. ein Mehraufwand von Wärme nothwendig sein
wird, um den gestörten Beharrungszustand der „freien“ Fahrt wieder zu
erreichen und zu erhalten.
Hieraus ist ersichtlich, daſs der Werth ηt, nach Gleichung XXIV berechnet, ein zu
günstiges Resultat ergeben muſs, und daſs dieses durch Anwendung des
Correctionsfactors c < 1, durch welchen eben „der Einfluſs der Stillstände und Aufenthalte in
den Stationen“ berücksichtigt werden soll, zu rectificiren ist. Der Werth
c läſst sich a priori nicht berechnen, sondern nur
bestimmen aus Gleichung XXV.
XXV)
\eta_t=\eta_f.\left(\frac{T_0-T_2}{T_0}\right)\,\xi.c.
Für Dauerfahrten ohne Unterbrechungen wird c = 1 sein müssen, da sich nach Obigem ergibt, daſs der
Einfluſs der häufigen Fahrtunterbrechungen der Locomotive auf den Wirkungsgrad ihrer
Kesselanlage ein ungünstiger ist. Zum Nachweis des Werthes c, welcher für die vier Versuchsfahrten sehr nahe eine constante Gröſse
sein wird und zum Zwecke der Vorführung der Gröſsen
\eta_f.\frac{(T_0-T_2)}{T_0} und der nach den früheren
Gleichungen berechneten Correctionsfactoren ist die Tabelle XXIV aufgenommen.
Tabelle XXIV.
Art der Feuerung
Nepilly-Feuerung
Gewöhnliche Plan-feuerung
Zeichen der Versuchsfahrt
A
B
C
D
Wirkungsgrad des Feuer- raumes für den
Beharrungs- zustand der freien Fahrt
ηf
0,745
0,651
0,615
0,567
Theoretischer Wirkungsgrad der Heizfläche für den
Be- harrungszustand der freien Fahrt
\frac{T_0-T_2}{T_0}
0,781
0,794
0,750
0,761
Effectiver Wirkungsgrad der Heizfläche f.d.
Beharfungs- zustand der freien Fahrt
ηF . ξs . ξn
0,696
0,699
0,676
0,679
Correctionsfactoren
ξs
ξn
ξJ
ξ
10
0,9610,9290,9941,000
0,9590,9200,9950,999
0,9550,9430,9960,998
0,9650,9260,9960,996
Resultirender Corrections- factor
ξ
0,886
0,875
0,894
0,884
Absoluter Wirkungsgrad nach Gl. XXIV ohne
Berücksich- tigung der Störungen
ηt
0,505
0,453
0,413
0,382
Correctionsfactor
c
0,895
0,870
0,872
0,843
Einfluſs der Stillstände der Locomotive in den
Sta- tionen auf ηt
Δηt
0,053
0,059
0,053
0,060
Zusammenfassung.
Die in den Tabellen XXIII und XXIV zusammengestellten Schluſsergebnisse lassen
erkennen, daſs
1) der absolute Wirkungsgrad des Locomotivkessels im günstigsten Falle 45,2 Proc.
erreicht, wobei eine Anstrengung der Heizfläche von AF = 18k,59, eine solche der Rostfläche von AR = 444k,6 besteht, ferner ein Brennmaterial mit dem Heizwerthe H = 4369 Cal. verfeuert wurde. Dieser günstigste Fall
ist unter Anwendung der Nepilly-Feuerung (Fahrt A) erreicht worden, welche gegenüber der gewöhnlichen
Planfeuerung (bei sehr nahe gleichwerthigem Brennmaterial) (Fahrt C) einen Gewinn für den Wirkungsgrad der Kesselanlage
von 9,2 Proc. erreichen läſst, welcher sich auch durch das Verhältniſs der wahren
praktischen Verdampfungsziffern d.i. 3,04 : 2,48 = 1,214 sicher stellen läſst. Der
störende Einfluſs der Fahrtunterbrechungen in den Stationen beträgt übereinstimmend
5,3 Proc. Die Detailanordnung des Rostes für die Nepilly-Feuerung paſst befriedigend für das Format (Nuſskohle II) und die
maſsgebenden Eigenschaften der verwendeten Braunkohle.
2) Daſs der mindeste Werth des absoluten Wirkungsgrades derselben Kesselanlage (Fahrt
D) für dieselben Verkehrsverhältnisse 32,2 Proc.
erreicht, wobei eine Anstrengung der Heizfläche von AF = 15k,05, eine solche der Rostfläche von 462k,8
eintrat und bei Verwendung der gewöhnlichen Planfeuerung das verfeuerte
Brennmaterial (Braunkohle, Mittelkohle I) einen Heizwerth H= 4536 Cal. nachwies. Die erreichte wahre praktische Verdampfungsziffer
ist 2,28, der störende Einfluſs der Fahrtunterbrechungen in den Stationen beziffert
sich auf 6,0 Proc. Durch Ausnutzung der Nepilly-Feuerung bei nur wenig werth vollerem Brennmateriale und sonstig im
Wesentlichen unveränderten äuſseren Verkehrsverhältnissen ist (Fahrt B) ein Gewinn für den Wirkungsgrad der Kesselanlage von
7,2 Proc. zu erreichen; das Verhältniſs der bezüglichen Praktischen
Verdampfungsziffern beträgt 2,97 : 2,28 = 1,300. Die verfeuerte Mittelkohle I
fordert für ihre ökonomische Verbrennung andere Rostdetails als die angeordneten,
welch letztere dem Formate und den übrigen charakteristischen Eigenschaften der
Mittelkohle I nicht völlig entsprechen.
3) Der Wirkungsgrad des Feuerraumes, reducirt auf den Beharrungszustand der freien
Fahrt ηf erreicht im
günstigsten Falle (Fahrt A) 74,5 Proc. in Folge der
Anwendung der Nepilly-Feuerung und sinkt unter übrigens
sehr nahe denselben äuſseren Umständen (Fahrt C) um 13
Proc. auf 61,5 Proc. zurück. Bei Verfeuerung der Mittelkohle I ergibt sich bei
Anwendung der Nepilly-Feuerung ηf mit 65,1 und reducirt sich dieser
Werth bei Benutzung der gewöhnlichen Planfeuerung aber kräftigerer Kohle um 8,4
Proc., also auf 56,7 Proc. fallend.
4) Der effective Wirkungsgrad der Gesammtheizfläche (ηF), reducirt auf den Beharrungszustand der
freien Fahrt, ist für die entscheidenden Versuchsfahrten mit Nepilly-Feuerung (A und B) sehr nahe constant (69,6 und 69,9 Proc.),
desgleichen für die zwei Versuchsfahrten (C und D) mit gewöhnlicher Planfeuerung (67,6 und 67,9 Proc.)
also um etwa 2 Proc. geringer als für die Fahrten (A
und B).
5) Der resultirende Correctionsfactor ξ in Folge
Strahlung, Dampfnässe, Benutzung des Injectors und des Kesselwassers zum Einspritzen
in die Rauchkammer ist für die vier Versuchsfahrten sehr nahe constant und im Mittel
ξm = 0,885.
6) Berücksichtigt man endlich die von Prof. Grove
ermittelten charakteristischen Werthe für die Bestimmung des absoluten
Wirkungsgrades des Locomotivkessels u.s.w. für Koks-
und Steinkohleheizung und stellt diese mit den analogen
Mittelwerthen, welche für die in Rede stehenden vier Versuchsfahrten mit Braunkohleheizung für den Beharrungszustand der freien
Fahrt gewonnen wurden, zusammen, so ergeben sich endlich die in die Tabelle XXV
aufgenommenen Schluſswerthe.
Tabelle XXV.
Verhält-niſswerthe
Koks-heizung
Steinkohle-heizung
Braunkohleheizung
Nepilly-Feuerung
GewöhnlichePlanfeuerung
Ft : R
70
70
73
70
B : R
500
450
412
476
T2°
Cels.
528,0
467,0
290,5
304,0
Mn : B
5,7
5,6
4,91
4,05
Mt . B
–
–
3,0
2,38
ηt
0,6
0,52
0,423
0,34