| Titel: | Selling's Rechenmaschine; von Direktor Dr. A. Poppe. |
| Autor: | A. Poppe |
| Fundstelle: | Band 271, Jahrgang 1889, S. 193 |
| Download: | XML |
Selling's Rechenmaschine; von Direktor Dr. A. Poppe.
Mit Abbildungen im Texte und auf Tafel 10.
Selling's Rechenmaschine.
Seit mehr als zwei Jahrhunderten haben sich die geistreichsten und scharfsinnigsten
Köpfe, Gelehrte wie Pascal, Leibnitz u.a. mit der
Lösung der Aufgabe beschäftigt, die geistlose, ermüdende und erschlaffende Arbeit
des anhaltenden Zifferrechnens durch eine Maschine verrichten zu lassen, ohne ihre
Bemühungen und Opfer von einem namhaften Erfolge begleitet zu sehen. Erst unserem
Jahrhunderte war ein entschiedener Fortschritt auch in dieser Richtung vorbehalten.
Hiervon legt u.a. die aus den fünfziger Jahren stammende Scheutz'sche RechenmaschineVgl. 1860 156 241. 321. ein glänzendes
Zeugniſs ab. Von einer Verbreitung dieser merkwürdigen, 10 englische Centner
wiegenden Maschine, deren Anschaffungskosten sich auf nicht weniger als 2000 Pfd.
Sterl. (40000 M.) belaufen sollen, kann jedoch begreiflicher Weise keine Rede sein,
selbst von dem Umstände abgesehen, daſs sie nicht zur Ausführung beliebiger
Rechnungen, sondern nur zur Herstellung tabellarischer Werke, wie Logarithmen,
dient. Die erste Rechenmaschine, welche in weiteren Kreisen Eingang gefunden und
sich als Hilfsmittel für Mathematiker, Astronomen, Versicherungsgesellschaften
u.s.w. bis auf den heutigen Tag behauptet hat, ohne jedoch zu einer dem Bedürfnisse
genügenden Verbreitung zu gelangen, ist der dem Elsässer Thomas bereits im J. 1820 patentirte „Arithmomètre“.Eine das Wesentliche umfassende Beschreibung dieser Maschine von F. Reuleaux befindet sich in D. p. J. 1862 165 *
334.
Der Thomas'sche Arithmometer ist es, dessen sich Herr
Dr. Selling, Professor der Mathematik und Astronomie an
der Universität Würzburg, bei seiner Untersuchung über die Leistungsfähigkeit des
allgemeinen Unterstützungsvereines für die Hinterlassenen der bayerischen
Staatsdiener und der mit demselben verbundenen Töchterkasse bedient hat, wozu zum
ersten Male Tabellen der Ueberlebungsrenten der Kinder über beide Eltern berechnet
und benützt worden sind. Mit Hilfe des Arithmometers ist es ihm möglich geworden,
die gewaltigen Ziffermassen bei Berechnung so zahlreicher Tabellen in zwei Jahren zu
bewältigen. Bei dieser Riesenarbeit hatte Dr. Selling
reichlich Gelegenheit, sich von dem groſsen Nutzen der sinnreichen Maschine zu
überzeugen. Aber auch ihre Mängel sind seinem Scharfblicke nicht entgangen, und
diese fand er hauptsächlich in der Ungleichmäſsigkeit und zeitweisen Häufung der
Widerstände, sowohl bei Bildung der Theilproducte, als auch bei der sogen.
Zehnerübertragung. Unwillkürlich drängte sich ihm die Frage auf, ob es denn nicht
möglich sei, die Construction des Arithmometers mit ihrer intermittirenden,
stoſsenden und rasselnden Bewegung, durch eine solche von gleichmäſsigem, sanftem
und geräuschlosem
Gange zu ersetzen. Nach jahrelanger beharrlicher Arbeit und Ueberwindung mancher
technischen Schwierigkeit ist ihm die Lösung dieser Aufgabe in überraschend schöner
Weise durch die Erfindung seiner Rechenmaschine (D. R. P. Nr. 39634 vom 16. April
1886) gelungen, welche eine Fülle ebenso geistvoller als praktischer Gedanken
vereinigt.In der Broschüre: E. Selling, Eine neue
Rechenmaschine. Berlin. Springer.
1887, findet man als Einleitung eine kurz gefaſste Geschichte der
Rechenmaschinen überhaupt, sodann die Beschreibung der
ursprünglichen Construction seiner eigenen Rechenmaschine, mit ihren
möglichen Aenderungen.
Fig. 1., Bd. 271, S. 194
I. Beschreibung der Maschine.
Die allgemeine Constructionsanlage ist aus der nach einer photographischen Aufnahme
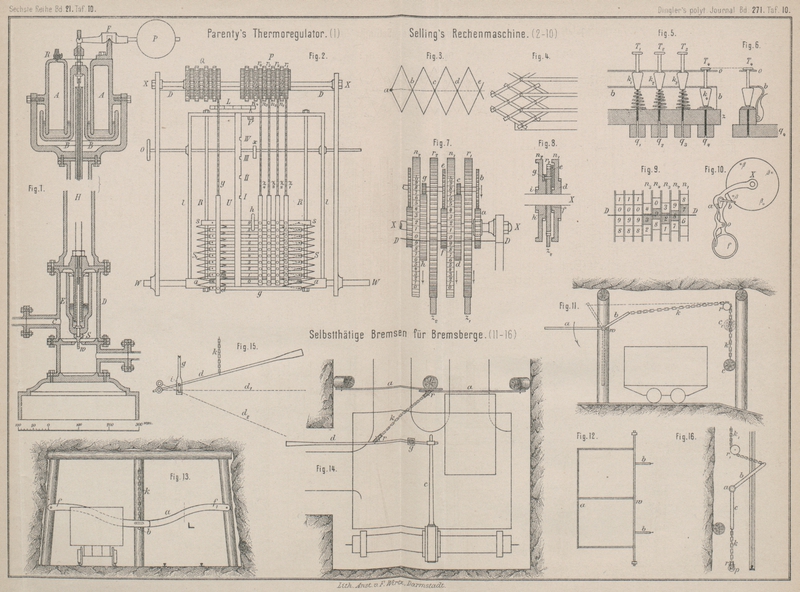
ausgeführten Textabbildung, sowie aus dem schematischen Grundrisse (Fig. 2 Taf. 10)
ersichtlich. Schon ein Blick auf diese Figuren läſst den eigenartigen, von allen
anderen bekannten Systemen völlig abweichenden Charakter der Selling'schen Rechenmaschine erkennen. Sie beruht im Wesentlichen auf zwei
Prinzipien, dem einen zur Bildung der Theilproducte, dem anderen zur
Zehnerübertragung.
A) Bildung der Theilproducte. Die Einführung der unter
der Bezeichnung „Nürnberger Schere“ bekannten rhombischen Gelenkverbindung,
als Mittel zur Bildung der Theilproducte, ist ein ebenso glücklicher als origineller
Gedanke. Fig.
3 Taf. 10 stellt die Nürnberger Schere in ihrer einfachsten Form
schematisch dar. Ihr Prinzip ist mit wenigen Worten erklärt. Wenn der Punkt a festgehalten, und der erste Kreuzungspunkt b längs der Mittellinie um 1 Einheit verschoben wird,
so bewegen sich die folgenden Kreuzungspunkte c, d,
e... bezieh. um 2, 3, 4... Einheiten. In Anwendung dieses Prinzipes sind zwei
vollkommen gleiche, in den Punkten aa festgehaltene
Nürnberger Scheren S und S1 (Fig. 2) an ihren
Kreuzungsstellen durch zehn Querstäbe 0, 1, 2, 3... 9 dergestalt mit einander verbunden, daſs sie längs
zweier Führungen RR durchaus gleiche Bewegungen machen.
Fig. 4
zeigt, wie ihre Gliederung der Verstärkung wegen in Wirklichkeit beschaffen ist.
Jenseits ihrer festen Punkte sind die Scheren um eine Gelenkverbindung erweitert,
deren Kreuzungspunkte durch einen elften Querstab g
verbunden sind. Dieser bewegt sich in einer den Verschiebungen der Doppelschere
entgegengesetzten Richtung. Sein Zweck wird später erklärt werden. Die Fixpunkte aa der Schere liegen auf dem vierkantigen Theile einer
Welle WW, welche mit dem Rahmen ll ein festes Ganze bildet. Ihre Enden sind in einem auf den
Führungsstangen R R gleitenden Schieber ss gelagert, welcher mittels des Handringes h vor oder zurück bewegt werden kann, wenn man die
Schere öffnen oder schlieſsen will. Dehnt man nun die letztere so weit aus, daſs der
Querstab i den Weg w
zurücklegt, so sind die von den Querstäben 2, 3, 4... 9
zurückgelegten Wege 2w, 3w, 4w... 9w. Die Querstäbe werden rechtwinkelig gekreuzt von
neun auf ihnen liegenden Zahnstangen Z1, Z2, Z3... Z9,
wovon jedoch in Fig.
2 nur vier angegeben sind. Der ungezahnte Theil jeder Zahnstange hat zehn
gleichweit von einander abstehende Löcher, welche bei der in Fig. 2 dargestellten
Anfangslage der Schere direkt über entsprechenden Löchern der Querstäbe zu liegen
kommen. Jedes der Zahnstangenlöcher enthält einen oben mit einem Knöpfchen
versehenen Stahlstift, welcher, wenn er wie eine Taste hinabgedrückt wird, die
betreffende Querstange mit der Zahnstange verbindet. Bezeichnet man die Stifte oder Tasten mit den
Nummern der Querstäbe, über denen sie liegen, so braucht man, um z.B. die Zahl 571
einzustellen, nur die Taste 1 der Zahnstange Z1, die Taste 7 der Zahnstange Z2 und die Taste 5 der
Zahnstange Z3
hinabzudrücken. Dadurch sind die drei Zahnstangen mit den betreffenden Querstäben
verbunden, so daſs sie beim Oeffnen der Schere die den Ziffern der gegebenen Zahl
entsprechenden Wege 1w, 7w, 5w der Querstäbe mitmachen,
während die übrigen mit dem unbeweglichen Nullstabe aa
verbundenen Zahnstangen zurückbleiben.
Soll eine neue Zahl an der Claviatur eingestellt werden, so braucht man auf die
vorher eingestellt gewesenen Ziffern keinerlei Rücksicht zu nehmen, indem der
betreffende Stift durch einen sinnreichen Federmechanismus von selbst in die Höhe
springt und auſser Eingriff kommt, sobald ein anderer derselben Zahnstange
hinabgedrückt wird. Die Fig. 5 und 6 veranschaulichen diesen
Hilfsmechanismus in zwei senkrechten Durchschnitten, q1, q2, q3, q4 sind vier Querstäbe der in Nullstellung
befindlichen Schere, T1, T2, T3, T4 ebenso viele in
einer Führung oo gleitende Tasten, wovon die eine
hinabgedrückt ist, um die Zahnstange ZZ mit dem
Querstabe q4 zu
verbinden. Jede Taste besitzt eine kleine kegelförmige Erweiterung, auf welche von
unten eine Spiralfeder wirkt und die Taste nach oben drängt. Beim Hinabdrücken der
Taste T4 hat der Kegel
k4 die vorstehende
Kante eines längs der Stiftenreihe sich hinziehenden, um eine Achse drehbaren und
elastisch andrückenden Bleches bb zurückgedrängt,
worauf die Kante, wie Fig. 5 zeigt, oberhalb des
Kegels eingeschnappt ist. Soll nun später an derselben Zahnstange eine andere Ziffer
eingesetzt und zu diesem Zwecke ein anderer Stift T1 hinabgedrückt werden, so schiebt k1 das Blech bb zurück, wodurch der Stift T4 frei wird und von selbst in die Höhe
springt, wogegen jetzt der niedergedrückte Stift T1 festgehalten wird. Es kann also nie eine und
dieselbe Zahnstange durch zwei Stifte gleichzeitig mit der Schere verbunden sein.
Das Einsetzen des Multiplicanden an der Claviatur nimmt auf diese Weise kaum so viel
Zeit in Anspruch, als das Anschreiben mit der Feder.
Ebenso schnell vollzieht sich die Bildung der Theilproducte einfach durch Oeffnen der
Scheren mittels des Handringes h (Fig. 2). Zur genauen
Begrenzung dieser Bewegungen dient die Scala U mit den
vier kleinen den Multiplicatorziffern 1, 2, 3, 4 entsprechenden Einschnitten I, II, III, IV, indem durch eine leichte Drehung des
Handringes h ein Riegel frei wird und in einen der
Einschnitte einschnappt. Der Ziffer 5 entspricht ein Anschlagen des Schiebers s an den Aufhaltstift V.
Die Fortsetzung der Multiplicatorscala bis zur neunten Haltstelle hat der Erfinder
nicht für nothwendig erachtet, da man den Ziffern 6, 7, 8, 9 bezieh. die Werthe (10
– 4), (10 – 3), (10 – 2), (10 – 1) oder auch (2 + 3), (3 + 4), (3 + 5), (4 + 5)
substituiren kann. Es ist dies jedoch nicht nothwendig und geschieht nur, um die
Längendimensionen der Maschine zu vermindern und kleinere Bewegungen zu erzielen.
Der ganze um WW drehbare Rahmen kann um einen kleinen
Bogen gehoben und gesenkt werden. Dieses geschieht durch Drehung des Handknopfes O, dessen Achse im Rahmen ll gelagert ist und ein Excenter x enthält,
welches auf der im Gestelle befestigten runden Stange u
(Fig. 1)
aufliegt. Durch Hebung des Rahmens gelangen die Zahnstangen mit den Zahnrädern r1, r2, r3... des Systemes P in Eingriff, um ihre den Theilproducten
proportionalen Längsverschiebungen in Drehungen dieser Räder umzusetzen. Die Senkung
des Rahmens bringt sie wieder auſser Eingriff.
B) Die Zehnerübertragung. Das Radsystem P besteht bei der in Fig. 1 abgebildeten
Rechenmaschine aus 13 gleichen Zahnrädern r1, r2, r3... jedes von 36 Zähnen, und ebenso vielen
Zifferrädern n1, n2, n3... von etwas
gröſserem Durchmesser. Sämmtliche Räder sitzen in wechselnder Reihenfolge lose auf einer gemeinsamen, an das Gestell festgeschraubten Achse XX.
Diese trägt noch ein zweites, gleichfalls mit Zehnerübertragung ausgestattetes
Radsystem Q, bestehend aus sieben Zahnrädern und sieben
Zifferrädern. Von diesem mag vorläufig nur so viel gesagt werden, daſs dasselbe in
Verbindung mit der einzelnen Zahnstange y bei
Multiplicationen den Multiplicator, bei Divisionen den Quotienten registrirt. Der
cylindrische Umfang der Zifferräder ist durch Querstriche in 40 gleiche Felder
getheilt, welche die zehn in erhabener Schrift gravirten Ziffern 0 bis 9 in
vierfacher Folge aufnehmen. Dicht über das ganze Radsystem ist parallel zur Achse
ein Faden DD als Index gespannt, welcher bei
Nullstellung der Räder den unteren Strich jedes Nullfeldes deckt. An diesem Faden
erscheint nach beendigter Rechnung in dem Einschnitte des Schutzbleches A (Fig. 1) das Resultat. Da
aber die Ziffern 1, 2, 3... 9 in vierfacher Folge auf den Radumfängen vorhanden
sind, so bilden sich die Resultate nicht nur längs der Ableselinie DD, sondern auch von 90° zu 90° längs dreier anderer
Linien. Dies kann dazu benützt werden, um auf der Rückseite der Räder das Resultat
mittels einer besonderen Vorrichtung, wozu die Walze cc
und das Rädchen d (Fig. 1) gehört, auf einem
Papierstreifen als Rechnungsbeleg abzudrucken.
Angenommen nun, die an der Claviatur eingesetzte Zahl 875 solle fürs erste einfach
als solche auf die Räder übertragen, d.h. mit 1 multiplicirt werden, und die
betreffenden Zahnstangen Z1, Z2, Z3 befinden sich mit
den Rädern r1, r2, r3 in Eingriff, so
öffnet man die Schere aus ihrer Anfangslage bis zum Einschnitte I der Scala U. Die
Zifferräder n1, n2, n3 werden alsdann in
entsprechender Richtung bezieh. um 5, 7, 8 Ziffern weiterrücken, und an Stelle der
drei Nullen wird der Multiplicand 875 am Faden DD
erscheinen. Soll dieselbe Zahl mit 4 multiplicirt werden, so öffnet man die Schere
von ihrer Nullstellung aus bis zum Scaleneinschnitte IV.
Da aber die Ziffern der Räder nur von 0 bis 9 gehen, während die Wege der
Zahnstangen Z1, Z2, Z3 im gegebenen Falle
bezieh. den 20fachen, 28fachen und 32fachen Ziffernabstand darstellen, so muſs für
die Zehnerübertragung von einem Zifferrade auf das links nächste gesorgt sein. Die
Methode dieser Uebertragung gehört zu den feinsten Eigenthümlichkeiten der Selling'schen Rechenmaschine. Sie besteht in einem
Mechanismus, mittels dessen jedes Zifferrad stetig um 1/10 der Drehung des rechts nächsten in
derselben Richtung sich dreht, neben dieser Drehung aber und ganz unabhängig von ihr
noch diejenige Bewegung annimmt, welche durch die Zahnstangen unmittelbar eingeführt
wird. Zur Erklärung und Veranschaulichung dieses Vorganges dient Fig. 7, worin zwei
Zifferräder n1, n2 (Einerrad und
Zehnerrad), zwei Zahnräder r1, r2, nebst
den die Zehnerübertragung vermittelnden Elementen in der vorderen Ansicht und zwei
Zahnstangen Z1, Z2 im Querschnitte
dargestellt sind, und zwar der besseren Uebersicht wegen durch einen gröſseren
Zwischenraum von einander getrennt. Auf die feste Hauptachse XX ist ein Zahnrad a, das einzige
unbewegliche Rad des ganzen Systemes, festgekeilt, Auf diesem rollt ein gleich
groſses Planetenrad b, dessen Achse in der Wand des 36
Zähne enthaltenden Rades r1 excentrisch gelagert ist und an ihrem jenseitigen Ende ein Stahltrieb
c von 10 Zähnen trägt, b und c sitzen an ihrer Achse fest. Das Trieb
c steht mit dem an die eine Seite des Zifferrades
n1 befestigten
Zahnrade d von 100 Zähnen in Eingriff. Mit der anderen
Seite von n1 ist das
Zahnrad f fest verbunden, dessen Durchmesser dem des
Rades a gleich ist. Denselben Durchmesser besitzt das
auf dem Umfange von f rollende Planetenrad e dessen Achse in der Wand des Rades r2 gelagert ist und an ihrem anderen Ende ein Trieb
g von 10 Zähnen trägt, welches in das an n2 befestigte Rad h von
100 Zähnen greift. Die gleiche Räderverbindung wiederholt sich durch das ganze
System. Fig. 8
zeigt die Zifferräder n1, n2 mit dem
zwischenliegenden Zahnrade r2, dem Planetenräderpaare e, g und den an n1, n2 befestigten
Zahnrädern d, f und h, i
im senkrechten Durchschnitte längs der Achse, und zwar in der Hälfte ihrer
wirklichen Gröſse.
Angenommen nun, die Zahnstange Z1 (Fig. 7) ertheile dem Rade
r1 eine
vollständige. Umdrehung in der Pfeilrichtung, so hat sich während dieser das
Planetenrad b genau einmal um a gewälzt, also mit dem Triebe c eine
Umdrehung um seine Achse vollendet. Während dieser muſs daher vermöge des
Verhältnisses der Zähnezahl des Triebes c zu der des
Rades d das Zifferrad n1 eine rückläufige Bewegung von 1/10 Drehung
gemacht haben. Nun wird aber gleichzeitig die Achse des Räderpaares b, c vom Rade r1 mitgenommen, eine Bewegung, welche durch das jetzt
als Mitnehmer wirkende Trieb c auf das Einerrad n1 übertragen wird. Die
aus diesen beiden Bewegungen resultirende Drehung des letzteren nach der Pfeilrichtung ist also 9/10 der Drehung
von r1. Die Abstände
der Scaleneinschnitte von U (Fig. 1 und 2) sind so geregelt, daſs,
wenn die Zahnstange Z1
mit dem Querstabe i verbunden ist, die Bewegung der
Schere aus ihrer Nullstellung nach den Einschnitten I, II,
III... die Ziffern 1, 2, 3... des Einerrades genau an die Stelle der Null
bringt. Das Einerrad n1
theilt seine Drehung durch Vermittelung des Räderwerkes e,
f, g, h, dessen Dimensionen denen des Räderwerkes a, b, c, d vollkommen gleich sind, auf 1/10 reducirt, dem Zehnerrade n2 mit, und dieses
wieder seine Drehung, auf gleiche Weise reducirt, dem Hunderterrade n3 u.s.w. Daſs bei
dieser dem Zeigerwerke einer Uhr analogen Zehnerübertragung die Resultatziffern
nicht genau in einer Linie oberhalb des Indexfadens erscheinen können, sondern je
nach der Gröſse der rechts vorhergehenden Zahl schon theilweise unter den Faden
hinabgerückt sein müssen, läſst sich voraussehen. Um sich aber auch einen
anschaulichen Begriff von dem wirklichen Betrage dieser Abweichung zu machen, nehme
man an, die Zahl 39287 sei in die Claviatur eingesetzt und von da auf die
Zifferräder übertragen worden. Bezeichnet man zuvörderst die Einer, Zehner,
Hunderter u.s.w. der gegebenen Zahl bezieh. mit a, b, c, d,
e und setzt die Bogenlänge eines Zifferfeldes = 1, so ist der Betrag, um
welchen der untere Strich des Feldes den Faden überschritten hat:
Bei
n_1=0
„
n_2=\frac{a}{10}
„
n_3=\frac{a}{10}+\frac{b}{10}
„
n_4=\frac{a}{1000}+\frac{b}{100}+\frac{c}{10}
„
n_5=\frac{a}{10000}+\frac{b}{1000}+\frac{c}{100}+\frac{d}{10}
Für die Zahl 39287 würden sich diese Ueberschreitungen herausstellen, wie folgt:
Bei
n1 = 0
„
n2 = 0,7
„
n3 =
0,87
„
n4 =
0,287
„
n5 =
0,9287
und danach die betreffenden Ziffern etwa wie in Fig. 9 sich
gruppiren, wenn man sich die Räder nahe an einander gerückt denkt. Jede etwaige
Unsicherheit in der richtigen Ablesung des Resultates wird durch die Beobachtung
folgender Regel gehoben: Die richtige Ziffer ist immer
diejenige, bei welcher entweder der untere Strich ihres Feldes mit dem
Indexfaden zusammenfällt (wie bei 7), oder deren Feld von dem Faden geschnitten wird.
Da das Auge gewohnt ist, jedes Rechnungsresultat in einer Reihe geordnet zu sehen, so könnte
jene Abweichung aus der Richtung neben einem gewissen Gefühle der Unsicherheit ein
ästhetisches Bedenken erregen. Der vorurtheilsfreie Rechner wird sich aber, sobald
er die Ueberzeugung gewonnen hat, daſs jene kleine Unregelmäſsigkeit auf die
richtige Erkenntniſs des Resultates keinen Einfluſs hat, bald daran gewöhnen. Der
Erfinder selbst bezeichnet diese Art der Ablesung sogar als einen Vortheil. Das Bild
der Zahl sei in gewisser Weise ein organisches Gefüge, worin kein Theil ohne alle
übrigen verändert werden könne. Jede Ziffer sei durch die Stellung des links
vorausgehenden Zifferrades controlirt. Nachdem man sich einmal an diese Ablesung
gewöhnt habe, würde man sie ungern vermissen, weil sie viel mehr das Gefühl der
Sicherheit gebe, als wenn jede Ziffer nur für sich steht. In der automatischen Copie
dagegen, welche ihrer Bestimmung gemäſs auch Anderen, die mit der Maschine selbst
nicht vertraut sind, zur Revision vorgelegt werde, sei es allerdings wünschenswerth,
die Rechnungsresultate in der gewöhnlichen Form zu erhalten. Von diesem
Gesichtspunkte ausgehend hat der Erfinder einen zur Zeit in Ausführung begriffenen
Mechanismus in der gemeinnützigen Wochenschrift des
polytechnischen Centralvereines für Unterfranken und Aschaffenburg mit
Abbildung angegeben, welcher das Gewünschte leistet, ohne daſs die stetige Bewegung
und die Möglichkeit der bisherigen Ablesung verloren geht.
C) Hilfsvorrichtungen. Bevor ich zur Ausführung der für
das Geschäftsleben wichtigsten Rechnungsoperationen mit der Selling'schen Maschine übergehe, sind noch einige wichtige
Hilfsvorrichtungen zu beschreiben. Der Rahmen II kann
mittels des Handknopfes O nicht nur gehoben und
gesenkt, sondern auch mit der Welle WW seitwärts
verschoben werden. Diese Verschiebung hat den Zweck, die Zahnstangen beim Uebergange
der Multiplication von den Einern auf die Zehner, Hunderter u.s.w. mit den nächsten
links liegenden Rädern in Eingriff zu bringen. Zur Controle dieser Einstellung dient
bei den neuesten Apparaten (statt der in die Einschnitte der Achse WW (Fig. 1) einschnappenden
Feder) die Scale L (Fig. 2), deren
Theilstriche genau denselben Abstand von einander haben, wie die Zahnräder. Man
braucht daher nur jedesmal einen an dem Rahmen angebrachten Zeiger von einem
Theilstriche zum nächstfolgenden zu führen. Dieses bedarf keiner besonderen
Aufmerksamkeit, indem sich der Eingriff der Zahnstangen, auch wenn der Zeiger nicht
genau auf dem betreffenden Theilstriche stehen sollte, am richtigen Orte ganz von
selbst vollzieht. Unterhalb der Zahnräder ist nämlich parallel zur Achse eine
Schiene fest mit dem Gestelle verbunden, welche in denselben Abständen, wie die
Räder, eine Reihe nach unten sich erweiternder Einschnitte enthält. In einen solchen
Einschnitt legt sich nach jeder Verschiebung bei Hebung des Rahmens ein an diesem
befestigter Ansatz, wodurch die Eingriffslage gesichert ist.
Zur Sicherheit gegen jede Verrückung der Räder, während die Zahnstangen auſser
Eingriff sind, läuft parallel zur Achse XX ein Rechen
über das Radsystem, welcher durch Seitenstäbe mit dem Rahmen in starrer Verbindung
steht, also mit diesem sich hebt und senkt. Wenn nun in Folge der Senkung die
Zahnstangen auſser Eingriff kommen, legen sich gleichzeitig die Zähne des Rechens
zwischen je zwei Zähne eines Rades und halten dasselbe in fester Lage. Bei Hebung
des Rahmens greifen die Zahnstangen ein, und die Zähne des Rechens treten aus dem
Bereiche der Radzähne. Die Vorrichtung gestattet übrigens, um die Nullstellung der
Zifferräder zu ermöglichen, innerhalb eines kleinen Intervalles eine Mittellage, bei
welcher die Räder oben und unten frei sind.
Die Nullstellung aller Zifferräder wird durch eine
einzige Bewegung mit Hilfe der in Fig. 10 veranschaulichten
Vorrichtung bewirkt. Jedes Zifferrad enthält nämlich an seiner rechten Kante vier
kleine Stiftchen β in Abständen von 90° und überall
neben der gleichen Ziffer. In einem um die Hauptachse XX drehbaren Rahmen ist die Achse a eines
Rechens gelagert, dessen Zinken b für gewöhnlich nicht
bis an die Stifte β reichen. Legt man aber, nachdem
durch Beiseiteschiebung eines in Fig. 1 sichtbaren Bügels
g die oben erwähnte Mittellage der Vorrichtung zur
Sicherung der Radstellung herbeigeführt worden ist, den Finger in den Ring f, und drückt zugleich das Ende eines um o drehbaren Hebels, dessen anderer Arm auf einen
kleinen an der Achse des Rechens sitzenden Hebel wirkt, zurück, so kommen die
Stiftchen β sämmtlicher Zifferräder in den Bereich der
Zinken b. Dreht man zugleich den Ring in die Höhe, so
raffen die Zinken des Rechens die Stiftchen, denen sie jetzt begegnen müssen,
zusammen. Gleichzeitig dreht sich ein durch einen Gelenkmechanismus mit dem ersten
verbundener, anfangs um 180° von ihm abstehender zweiter Rechen in der
entgegengesetzten Richtung. Sobald dieser Abstand bis auf 90° sich vermindert hat,
so drücken die Zinken beider Rechen in entgegengesetzten Richtungen an je zwei
Stifte β und sichern dadurch die Stellungen der Räder,
wobei die Nullen in einer Reihe stehen. Zieht man alsdann den Finger zurück, so
bewegt sich der ganze Hilfsapparat unter dem Einflüsse geeignet angebrachter Federn
von selbst wieder in seine ursprüngliche Lage zurück.
II. Ausführung der Rechnungen.
Bei Betrachtung der Fig. 2 erkennt man sofort, daſs beim Oeffnen der Schere die Ziffern der
Räder P in ihrer natürlichen Folge 0, 1, 2, 3... 9,
also in additivem Sinne, beim Schlieſsen der Schere
dagegen in umgekehrter Ordnung 9, 8, 7... 0, also in subtractivem Sinne, die Ableselinie DD
passiren müssen. Da nun die Multiplication als wiederholte Addition, die Division
als wiederholte Subtraction aufzufassen ist, so kann erstere nur durch wiederholtes Oeffnen, letztere
durch wiederholtes Schlieſsen der Schere ausgeführt werden. Die einzelne Zahnstange
y ist daher, um den Multiplicator und Quotienten
auf den Rädern Q registriren zu können, bei der
Multiplication durch Niederdrücken der Taste m mit dem
Querstabe 1, bei der Division durch Niederdrücken der
Taste d mit dem Querstabe g zu verbinden, damit sie beim Oeffnen der Schere im ersten Falle das
betreffende Zahnrad in additivem, im letzteren Falle in subtractivem Sinne drehen
könne. Zur Vermeidung von Wiederholungen soll vor Beginn jeder Rechnung Alles auf
Null gestellt angenommen werden.
Addition. Um eine beliebige Anzahl Summanden zu addiren,
setzt man den ersten Summanden an der Claviatur ein, schiebt die Schere, um ihn auf
die Räder zu übertragen, von 0 bis zum Einschnitte I, während die Zahnstangen eingreifen, und zurück auf
0, während sie nicht eingreifen, Dasselbe
wiederholt man mit jedem folgenden Summanden. Die Summe kann schlieſslich an dem
Indexfaden abgelesen werden.
Subtraction. Wollte man auch eine Subtraction auf der
Rechenmaschine ausführen, so müſste man zunächst den Minuenden auf das Radsystem
übertragen, die Schere ohne Zahnstangeneingriff in die Nullstellung zurückziehen,
dann den Subtrahenden an der Claviatur einsetzen, die Schere ohne
Zahnstangeneingriff bis I öffnen und nach
bewerkstelligtem Eingriffe wieder bis 0
zurückziehen.
Multiplication. Es sei zu multipliciren 7548 mit 354.
Folgendes ist die Reihenfolge der Operationen:
1) Einstellung der Einzelstange y durch Niederdrücken
der Taste m auf Multiplication und des Multiplicanden
7548 an der Claviatur. Die vier schwarzen Tasten in Fig. 2 mögen die
betreffenden Ziffern bezeichnen.
2) Zahnstangen in Eingriff und Oeffnen der Schere wegen des Multiplicators 4 bis zum Einschnitte IV.
Auf den Zifferrädern n1, n2, n3, n4, n5 erscheint am Faden
DD die Zahl 30192 als erstes Zwischenresultat,
welches man weiter nicht zu beachten braucht, und auf dem ersten Zifferrad des
Systemes Q die Multiplicatorziffer 4.
3) Zahnstangen auſser Eingriff und Zurückführung der Schere in ihre Nullstellung;
Verschiebung des Rahmens ll um eine Stelle nach links
und Hebung desselben, wodurch jede Zahnstange, statt in das bisherige Zahnrad, in
das links folgende eingreift.
4) Oeffnen der Schere wegen des Multiplicators 5 bis zum Anschlagstifte V. Am Indexfaden zeigt sich als zweites
Zwischenresultat die Zahl 407 592 und auf dem zweiten Zifferrade des Systemes Q die Multiplicatorziffer 5.
5) Wie in Nr. 3.
6) Oeffnen der Schere wegen des Multiplicators 3 bis zum Einschnitte III. Am Indexfaden erscheint das Endresultat: 2671992
und auf den Rädern Q steht der Multiplicator 354.
Demgemäſs erfordert die ganze Rechnung, nachdem der Multiplicand eingesetzt ist, nur
fünf sanfte Bewegungen. Denn die Operationen Nr. 3 und Nr. 5 lassen sich mit einer
einzigen zusammenhängenden Bewegung ausführen. In vorstehendem Beispiele geht keine
der Multiplicatorziffern über 5 hinaus. Ist aber die eine oder die andere derselben
gröſser als 5, so kann man sich dieselbe in zwei Summanden zerlegt denken, z.B. 8 in
3 + 5. Das Verfahren unterscheidet sich alsdann von dem vorhergehenden Beispiele nur
dadurch, daſs jetzt die Schere wegen einer Multiplicatorziffer zweimal zu öffnen
ist. Man kann aber auch den Multiplicator 8 ebenso gut durch (10 – 2) ausdrücken,
also von dem Zehnfachen des Multiplicanden, welches sich durch Verschiebung des
Rahmens um eine Stelle nach links ergibt, das Zweifache desselben subtrahiren.
Uebrigens wird jeder verständige Rechner, auch wenn er mit einem Apparate arbeitet,
bei welchem die Multiplicatorziffern bis 9 unmittelbar angewandt werden können,
passende Gelegenheiten zur Abkürzung des Verfahrens nicht vorübergehen lassen. Er
wird z.B. den Multiplicator 697 durch 700 – 3 sich ausgedrückt denken, den Rahmen um
zwei Stellen nach links verschieben, mit 7 multipliciren und schlieſslich den
dreifachen Multiplicanden subtrahiren.
Division. Das praktische Verfahren bei der Division
ergibt sich naturgemäſs aus ihrer Auffassung als wiederholte Subtraction, wonach der
Quotient die Zahl ist, welche anzeigt, wie vielmal der Divisor vom Dividenden
subtrahirt werden kann. Vor der Ausführung schiebt man den Rahmen nach links, so
daſs die Zahnstange Z9 unter das vorletzte, und die
Einzelstange y unter das letzte Zahnrad der
betreffenden Systeme P und Q zu liegen kommt.
Es sei z.B. 92742 zu dividiren durch 396. Die Reihenfolge der Operationen ist
diese:
1) Einstellen des Dividenden 92742 an der linken Seite der Claviatur und Uebertragen
desselben durch Oeffnen der Schere bis I auf das
Radsystem P.
2) Schere ohne Eingriff zurück in die Ruhelage und Einstellen des Divisors 396 an der
Claviatur.
3) Verbindung der Einzelstange y, durch Niederdrücken
der Taste d, mit dem Querstabe g, damit sich die mit y in Eingriff kommenden
Räder des Systemes Q in additivem Sinne drehen. Oeffnen
der Schere ohne Eingriff bis zum Anschlage V.
4) Rückführung der Schere mit Eingriff, bis man an der höchsten Stelle des Dividenden
Null erscheinen sieht.Wenn der Spielraum der Schere nicht hinreicht, um die Null mit einer Rückbewegung derselben an den Indexfaden
zu bringen, so wiederholt man diese Operation bis zum Erscheinen der
Null. Gleichzeitig mit dieser zeigt sich auf dem letzten
Zifferrade des Systemes Q die erste Quotientenziffer
2. An der Stelle des
gegebenen Dividenden steht jetzt als erster Rest 13542.
5) Zahnstangen auſser Eingriff und seitliche Verschiebung um eine Stelle nach rechts.
Rückschiebung der Schere mit Eingriff', bis statt der Ziffer 1 der Zahl 13542 Null
erscheint. Mit dieser zugleich zeigt sich im vorletzten Zifferrade des Systemes Q die zweite Quotientenziffer 3, und an Stelle von
13542 steht jetzt 1662 als zweiter Rest.
6) Zahnstangen auſser Eingriff und Verschiebung um eine Stelle nach rechts.
Rückführung der Schere mit Eingriff', bis statt der Ziffer 1 der Zahl 1662 Null
erscheint. Im Systeme Q kommt gleichzeitig 4 als dritte
Quotientenziffer zum Vorscheine und in P steht 78 als
dritter und letzter Rest am Indexfaden.
Resultat: Der Quotient ist 234 und der Rest 78.
Vorstehende Zusammenstellung der Rechnungsvorschriften für die vier Species dürfte
für die Geschäftspraxis genügen und den intelligenten Rechner in den Stand setzen,
sich die Regeln für verwandte Fälle, wie Wurzelausziehung u.s.w., selbst zurecht zu
legen. Daſs die Einübung auf den Dienst der Selling'schen Rechenmaschine mehr Zeit als die Erlernung der Handhabung des
Arithmometers erfordert, ist nicht in Abrede zu stellen. Hat man aber einmal eine
gewisse Fertigkeit in den Handgriffen und Sicherheit in ihrer Aufeinanderfolge
erlangt, so führt sie rascher zum Ziele, als das Arithmometer. Unter den von Dr. Selling dem letzteren gegenüber geltend gemachten
Vortheilen seines Instrumentes sind besonders folgende hervorzuheben:
1) Alle Bewegungen, sowohl bei der Bildung der Theilproducte, als auch bei der
Zehnerübertragung sind durchaus gleichmäſsig, sanft und geräuschlos; sie sind ebenso
leicht rückwärts wie vorwärts auszuführen.
2) Die Einstellung des Multiplicanden, Divisors u.s.w. geschieht durch einfaches
Niederdrücken von Tasten, wobei man auf die vorher eingesetzt gewesene Zahl keine
Rücksicht zu nehmen braucht.
3) Die Multiplication einer beliebigen Zahl mit irgend einer Ziffer, wozu bei dem
Arithmometer so viel Kurbeldrehungen nöthig sind, als die Multiplicatorziffer
Einheiten enthält, ist mit einer einzigen Handbewegung abgemacht.
4) Die Nullstellung einer beliebigen Zifferreihe vollzieht sich auf einen Griff.
5) Zur Sicherung der Radstellung sind nirgends Sperrfedern, wie bei der Thomas'schen Maschine, sondern ausschlieſslich starre
Körper benützt.
6) Alle eingesetzte Zahlen, Zwischen- und Endresultate können durch eine einzige
Handbewegung copirt werden.
7) Bei Selling's Rechenmaschine geht die
Zehnerübertragung durch alle Radsysteme hindurch, während sie im Arithmometer bei
der zweiten Stelle links vom Multiplicanden aufhört.
8) In Folge der Gleichmäſsigkeit der Widerstände kann die Stellenzahl bei nur
mäſsiger Preiserhöhung bis zu fast beliebiger Ausdehnung vergröſsert werden.
Ich darf übrigens nicht unerwähnt lassen, daſs es Herrn Arthur Burkhardt in Glashütte, dessen Verdienste um die Verbesserung des
Arithmometers bekannt sind, gelungen ist, den unliebsamen Folgen der unzulänglichen
Zahnerübertragung durch Anbringung eines Zehner-Ergänzungs-Signales
vorzubeugen.Auf das Bedürfniſs eines der Zehnerübertragung beizugebenden akustischen
Signales hatte Dr. Selling schon in der oben
erwähnten Broschüre S. 49 aufmerksam gemacht.
Prof. Selling hat die Herstellung seiner neuen
Rechenmaschine für Deutschland dem Mechaniker Max Ott
in Kempten übertragen. Sie ist in guten Händen; denn Herr Ott hat den Geist der Erfindung mit klarem Verständnisse erfaſst. Aus
seiner Werkstätte für Präcisions-Mechanik ist bereits eine Anzahl Exemplare in
untadelhafter Ausführung hervorgegangen.
Die Maschine, wie sie Fig. 1 darstellt, ist 35cm breit, 40cm lang und 15cm
hoch. Sie gestattet die Multiplication einer 9 stelligen Zahl noch mit einer
7stelligen, während das Product auf 13 Stellen genau abzulesen ist. Ihr Preis
beträgt 400 M.
Tafeln