| Titel: | E. Roche's Zeiger- und Schnellwage. |
| Autor: | Pr. |
| Fundstelle: | Band 271, Jahrgang 1889, S. 305 |
| Download: | XML |
E. Roche's Zeiger- und Schnellwage.
Mit Abbildungen im Texte und auf Tafel 14.
Roche's Zeiger- und Schnellwage.
Die Eigenthümlichkeit dieser Wage besteht in der Anordnung des Zeigerwerkes und in
der Verbindung desselben mit einer eingetheilten Hebelschiene und Laufgewicht, so
daſs auf der letzteren die groſsen Gewichtslasten abgelesen, während durch den
Zeiger die Einheiten angegeben werden. Der Genauigkeitsgrad soll hierdurch bis auf
\frac{1}{4000} des Gesammtlast steigen, während für die
gewöhnlichen Zeiger oder Schnellwagen gesetzlich in Frankreich nur
\frac{1}{1000} Empfindlichkeit vorgeschrieben ist (vgl. Guillaumin 1888 269 * 496).
Nach Le génie civil, 1888 * 380, besteht diese Wäge
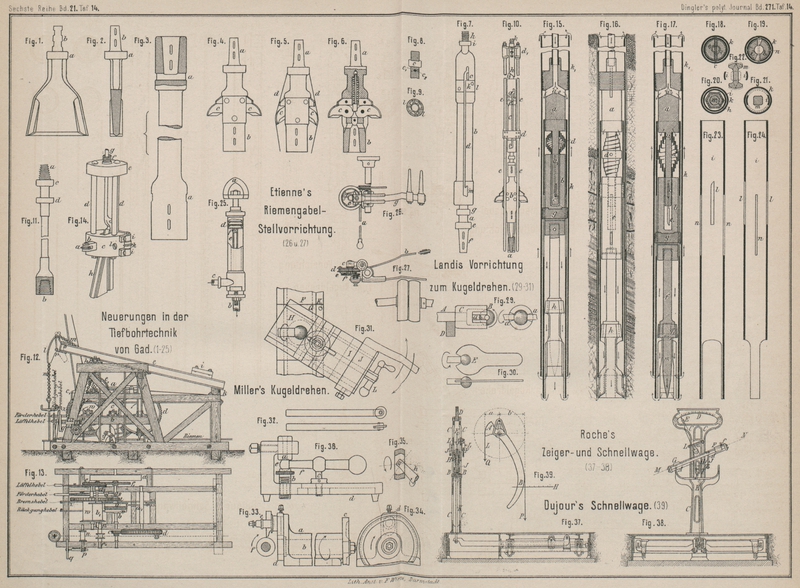
Vorrichtung, welche an einer Brückenwage angeordnet ist, aus der Standsäule C (Fig. 37 und 38 Taf. 14)
mit den Lagerpfannen O und dem Zeigerblatte D. An dem um 0
schwingenden Hebel MN ist die Hängeschiene J durch Vermittelung eines Parallelhebelwerkes IB und hieran die Hängestange K, welche die Verbindung mit den Brückenhebeln herstellt, angelenkt.
Winkelrecht zu MN und durch das Schwingungsmittel
gerichtet, ist der Zeiger E angeschraubt, welcher an
das kreisförmige Zeigerblatt D spielt, dessen
Gewichtseintheilungsstriche von seiner zugehörigen Kreisbogensehne nach dem später
zu erklärenden Verfahren abgetragen wird und nur zur bequemeren Ablesung bogenförmig
ausgebildet ist. Zur Herstellung einer standhaften Gleichgewichtslage dient das
Beschwerungsgewicht H, zur Ausgleichung und Regelung
das Schiebegewicht G, während zum Wägen groſser Lasten
(10 oder 100k) das mit dem Stellstifte f versehene Laufgewicht F verwendet wird.
Mit dem Schlieſshaken L wird die Wägevorrichtung
abgestellt.
Die Massenvertheilung des Gestänges ist nun in der Weise angeordnet, daſs in der
Nullstellung des Zeigers E die Hebelschiene die Lage
MN annimmt und hierbei jenen Lasten entspricht, die
durch die. Stellung des Laufgewichtes F auf der
Hebelschiene bedingt werden, also glatt 100, 200, 300k u.s.w. angibt, während die Zwischengewichte durch die Ausschwingungen
des Zeigers E angezeigt werden. Das Maſs dieser
Ausschwingung, sowie ihre Beziehung zur Last soll in der nachfolgenden Rechnung
begründet werden.
Fig. 1., Bd. 271, S. 306Fig. 2., Bd. 271, S. 306Es stelle in Textfig. 1 vor:
a Hebelarm der Last P; c
Hebelarm des Gegengewichtes q einschlieſslich dem
Schiebegewichte G : S
Schwerpunkt des Hebelwerkes bezieh. Angriffspunkt der Kraft q.
In der Nullstellung des Zeigers On muſs daher OS0 in die
Unterstützungslothrechten fallen. Zieht man ferner die Sehne nm senkrecht zur Zeigerrichtung OE = b, sobald die Hebelschiene MN (Fig.
38), d.h. der Hebelarm a (Fig. 1) in Folge einer
Belastung P wagerecht liegt, oder das Hebel werk sich
um den Winkel α gedreht hat, so entstehen bei einer
ferneren Drehung um den Winkel β; Abschnitte auf der
Sehne des Zeigerkreises, welche der Belastung P1 proportional sind.
Es ist
d = b . tg
α und x = b tg β
ferner
y = x +
d oder
y = x +
b . tgα 1)
Die Gleichgewichtsbedingung für den wagerechten Lastarm ist
0 = P . a – q . c sinα
und
q.c sinα = P . a 2)
Es ist ferner die Gleichgewichtsbedingung für die Last P1, entsprechend der weiteren Drehung um
den Winkel β:
0=P_1\,.\,\alpha\,.\,cos\,\beta-q\,.\,c\,sin\,(\alpha+\beta)
oder
q\,.\,c\,sin\,(\alpha+\beta)=P_1\,.\,\alpha\,.\,cos\,\beta
und
q\,.\,c\,.\,sin\,\alpha\,.\,cos\,\beta+q\,c\,.\,cos\,\alpha\,sin\,\beta=P_1\,\alpha\,cos\,\beta
bezieh.
q\,c\,sin\,\alpha+q\,c\,.\,cos\,\alpha\,.\,tg\,\ebta=P_1\,.\,a
q\,c\,.\,cos\,\alpha\,.\,tg\,\beta=P_1\,.\,\alpha-q\,.\,c\,.\,sin\,\alpha
endlich
Tg\,\beta=\frac{P_1\,a-q\,c\,sin\,\alpha}{q\,.\,c\,.\,\cos\,\alpha}
. . . . . . . . . . 3)
daher
x=b\,.\,tg\,\beta
und
x=b\,.\,\frac{P_1\,a}{q\,.\,c\,.\,cos\,\alpha}-b\,.\,tg\,\alpha
folglich
y=\frac{a\,.\,b}{q\,.\,c\,.\,cos\,\alpha}\,.\,P_1 . . . . .
. . . . . 4)
Weil aber \left(\frac{a\,.\,b}{q\,.\,c\,.\,cos\,\alpha}\right)
unveränderlich ist, so folgt die Proportionalität zwischen der Sehnenstrecke y und der Belastung P1. Es wird daher für P1
= o auch y = o, und für β = o (Gl. 3)
auch P1 = P werden.
Für sich allein würde aber die Zeigervorrichtung unzureichend sein, deſshalb ist
deren Verbindung mit der Hebelschiene sammt Laufgewicht vortheilhaft, indem die
Zeigerwage die Gewichtseinheiten, das Laufgewicht aber die Zehner oder Hunderte
angibt.
Ist MN (Textfig. 2) die
Hebelschiene und Q das Laufgewicht, so kann in irgend
einer Stellung, also auch in der Zeiger-Nullstellung nur Q und P2 in
Betracht kommen, deren Gleichgewichtsbedingung
0=P_2\,a-Q\,.\,l
lautet.
Die Gesammtbelastung ist aber
und
\left\{ {{P_2=\frac{l}{a}.Q\ \ \ \ \ \ \ \ \
}\atop{P_1=\frac{q\,.\,c\,.\,cos\,\alpha}{a\,.\,b}\,.\,y}}
\right.
also (P2 + P1).
Es ist schon früher erwähnt worden, daſs zur Bequemlichkeit der Zeigerablesungen die
gleich groſsen Gewichtsunterschieden entsprechenden gleich groſsen Sehnenabschnitten
(mn) einfach auf den Kreisbogen übertragen werden,
so daſs die Gewichtseintheilung am Zeigerbogen ungleichmäſsig und nach den
Schwingungsendpunkten zu abnehmend ausfällt. In den Ausführungen steht der Zeiger
winkelrecht zur Hebelschiene, daher die Bogensehne mn
wagerecht, weil der Zeiger OE lothrecht, bei
wagerechter Hebelschiene MN steht.
Pr.
Tafeln