| Titel: | Abhandlung über senkrechte, unterschlächtige Räder mit krummen Schaufeln, nebst Erfahrungen über die mechanischen Wirkungen dieser Räder; von Herrn J. V. Poncelet, Capitain des Geniewesens. |
| Fundstelle: | Band 19, Jahrgang 1826, Nr. CIII., S. 418 |
| Download: | XML |
CIII.
Abhandlung uͤber senkrechte,
unterschlaͤchtige Raͤder mit krummen Schaufeln, nebst Erfahrungen
uͤber die mechanischen Wirkungen dieser Raͤder; von Herrn J. V. Poncelet, Capitain des
Geniewesens.Wir hatten uns Anfangs vorgenommen, nur einen Auszug dieser wichtigen Abhandlung
mitzutheilen; nachdem wir aber reiflich hier uͤber nachdachten, fanden
wir es raͤthlicher, sie ganz zu liefern. Die Wasser-Raͤder sind an
den meisten unserer Werkstaͤtte ganz zuverlaͤssig nach den
fehlerhaftesten Grundsaͤzen gebaut; allein wer kennt nicht die Allmacht
des alten Herkommens? Wir wagen es nicht uns zu schmeicheln, daß die
nuͤzliche Verbesserung des Hm. Poncelet an
diesen Raͤdern den allgemeinen Beifall der Mechaniker finden wird, selbst
wenn sie die Beweise hieruͤber im Detail hier vor Augen gelegt sehen
werden. A. d. O. (Was in Frankreich gilt, wird wohl auch in Deutschland gelten.
Der Welsche sagt: „die ganze Welt ist Ein Land.“ Nach dem
Bulletin de la Société d'Encouragemenet
Nr. (CCLVII. S. 335 hat die Académie
royale des Sciences Hrn. Poncelet den von
Hrn. Moutyon gestifteten Preis fuͤr Mechanik,
eine goldene Medaille, 1000 Franken Werth, zuerkannt. Diese Abhandlung ist in
dem Bulletin gleichfalls in Extenso abgedrukt.
D.)
Aus den Annales de Chemie et de Physique T. XXX.
October. 1825. S. 136.
(Mit Abbildungen auf Tab.
X.)
Uebersezt von J. B. Fischer, M C.
Poncelet's, Abhandlung uͤber senkrechte,
unterschlaͤgige Raͤder.
Vorlaͤufige Betrachtungen.
Die gegenwaͤrtig am meisten gebraͤuchlichen
Wasser-Raͤder sind die senkrechten uͤberschlaͤchtigen
Raͤder oder Eimer-Raͤder, und die unterschlaͤchtigen
Schaufel-Raͤder. Die Einen wie die Anderen haben die Eigenschaft, daß sie nur
wenig Plaz fordern, leicht zu besorgen und auszubessern sind, und endlich die
Bewegung unmittelbar in einer senkrechten Ebene fortpflanzen, wie es der
groͤßte Theil der in den Kuͤnsten gebraͤuchlichen Maschinerien
erfordert.
Was die imaginaͤren oder neulich verbesserten horizontalen Raͤder, wie
das Danaidische, das Rad mit Centrifugal-Kraft, mit Ruͤkwirkung, und alle
jene Raͤder mit krummen Schaufeln betrifft, welche ein Ingenieur, Burdin, mit dem allgemeinen Ausdruke Kreisel- oder
Wirbelraͤder (turbines) bezeichnet hat, so
scheinen sie sich eigentlich mehr fuͤr jene Anstalten zu eignen, welche
geradezu eine umdrehende Bewegung in horizontaler Ebene mit einer großen
Schnelligkeit, erfordern, wie z.B. die Mehl-Muͤhlen und andere. Die
Schwierigkeiten, welche der Bau und die Unterhaltung dieser Raͤder
verursachen, die Groͤße des Raumes, welchen sie in horizontaler Richtung
brauchen, der unendlich kostspieliger ist, als jener, welchen man auf der
Hoͤhe des Gebaͤudes nehmen kann, beschraͤnken ihre Anwendung
vielfaͤltig, abgesehen davon, daß die Paris noch nicht genuͤgend
uͤber die Quantitaͤt der Wirkung aufgeklaͤrt ist, welche sie
mitzutheilen vermoͤgen. In der That, die Theorie gibt als Graͤnze oder
Maximum der Wirkung dieser Raͤder, eine Quantitaͤt von Wirkung an,
welche derjenigen gleich ist, die die bewegende Kraft besizt; allein; abgesehen von
der Unsicherheit der Daten, auf welche sich das Problem stuͤzt, bleibt es
keinem Zweifel unterworfen, daß diese Wirkung derjenigen wohl geleiteter und
gebauter, unterschlaͤchtiger Raͤder nachsteht.
Dieses sind wahrscheinlich die verschiedenen Gruͤnde, aus denen man sich
bisher, oder wenigstens in den meisten Faͤllen, an die senkrechten
Raͤder gehalten hat, von welchen ich oben sprach, und weßwegen man diese
bestaͤndig zu vervollkommnen und ihre Wirkungen kennen zu lernen suchte. Eben
diesem Streben nach Vervollkommnung verdankt man die senkrechten Raͤder, die
man Seitenraͤder nennt, welche man erst seit wenigen Jahren in den
Werkstaͤtten einfuͤhrte, und die, wie man sagt, sich von den Schaufel-
und Eimer-Raͤdern nur darin unterscheiden, daß das Wasser sich in einem
krummen Laufe bewegt, welcher einen Theil des Rades umfaßt, und dort nur in einem
Zwischenpuncte zwischen dem Gipfel und dem unteren Ende aufgefangen wird.
Die Vortheile der Seiten-Raͤder bestehen wesentlich darin, daß einerseits das
Wasser durch Druk wirkt, wie in den Eimer-Raͤdern, indem es folglich eine
groͤßere Wirkung ausuͤbt als in den Schaufelraͤdern, welche
durch Stoß, bewegt werden; und daß sie auf der anderen Seite faͤhig sind, den
kleinsten Fall des Wassers zu benuͤzen; was bei den oberschlaͤchtigen
nicht der Fall ist, deren Anwendung fast einzig auf jene Faͤlle
beschraͤnkt ist, welche 2–3 Meter uͤbersteigen, und nicht eine zu
große Menge Wassers liefern.
Ueberdieß haben die gewoͤhnlichen Schaufelraͤder den Vortheil einer
großen Einfachheit, allgemeinen Anwendbarkeit und vorzuͤglich der
Faͤhigkeit, sich mit großer Schnelligkeit zu bewegen, ohne sich von dem
Maximum der ihnen eigenen Wirkung zu entfernen, was bei den anderen nicht Statt
haben koͤnnte, ohne ihnen die Eigenschaft zu benehmen, einen groͤßeren
Theil der bewegenden Kraft zu ersparen.
Die Bedingung einer hinlaͤnglich großen Schnelligkeit, einer Schnelligkeit
z.B., welche 2 und 3 Meter uͤbersteigt, gruͤndet sich 1) darauf, daß
die Raͤder und die verschiedenen anderen Theile der Maschinerie, welche mit
derselben getrieben werden, dann Schwungraͤder bilden, oder mit einer
Quantitaͤt lebendiger Kraft begabt sind, die faͤhig ist, die
Einfoͤrmigkeit der Bewegung des Systemes, ungeachtet der Stoͤße, der
ungestuͤmen Veraͤnderungen der Schnelligkeit gewisser Stuͤke
und der periodischen Abwechslung der Wirkung des Widerstandes, zu erhalten; 2. daß,
da die arbeitenden Stuͤke der Maschine (les
opérateurs) fast immer eine betraͤchtliche Schnelligkeit zur
Erzeugung einer guten technischen Wirkung erfordern, zwischen Widerstand und Kraft
mehr oder weniger vervielfachte Triebwerke angebracht werden muͤßten, um
diese End-Geschwindigkeit zu erhalten, wenn das bewegende Rad langsam geht; so daß,
außer der Vermehrung der Kosten, daraus ein Zuwachs an passivem Widerstande, so wie
Hindernisse und Schwierigkeiten entspringen koͤnnten, welche unter gewissen
Orts-Verhaͤltnissen unuͤberwindlich waͤren.
Auch sieht man selten, daß selbst die Eimerraͤder, sich mit einer geringeren
Geschwindigkeit, als Ein Meter in der Secunde, bewegen. Fast immer gibt man ihnen,
im Gegentheile, eine Geschwindigkeit, die zwei Meter uͤbersteigt, ohne daß
man deßhalb diejenigen, welche sie gebaut, der Unwissenheit zu beschuldigen das
Recht hat; denn da der Fall des Wassers dann wenigstens 3 bis 4 Meter
betraͤgt, so bringen diese Raͤder eine Wirkung hervor, die jene der
best gebauten unterschlaͤchtigen Raͤder noch uͤbertrifft. Was
die Seiten-Raͤder betrifft, so weiß man, daß, in Folge des Spieles im Laufe
und der Geschwindigkeit, womit das Wasser zu entfliehen strebt, man dieselben nie
mehr als 2–3 Meter in Einer Secunde durchlaufen laͤßt, was fast
gaͤnzlich die Vortheile aufhebt, welche sie vor den gewoͤhnlichen Schaufel-Raͤdern
voraus haben, wann der Fall klein ist, z.B., zwei Meter und darunter.
Dieser verschiedenen Umstaͤnde wegen werden die gewoͤhnlichen
unterschlaͤchtigen Schaufel-Raͤder ungeachtet ihres wohl bekannten
Fehlers, nur einen kleinen Theil der Kraft, welche man ihnen vertraut,
zuruͤkzugeben, fortwaͤhrend in der Praxis angewendet,
vorzuͤglich in ebenen Laͤndern, wo das Gefaͤlle
natuͤrlich sehr gering, und die Wassermasse sehr betraͤchtlich ist,
und wo man sich folglich einen Fall von zwei Meter von oben herab nicht ohne
vorausgaͤngige, aͤußerst kostspielige Vorrichtungen, die unter
gewissen Ortsverhaͤltnissen oft auch unausfuͤhrbar sind, verschaffen
koͤnnte.
Wenn man also nicht gaͤnzlich das Licht der Praxis verbannen will, welcher
doch selbst so viel daran liegt, die Naturkraͤfte auf das moͤglich
Beste zu benuͤzen, so fuͤhlt man sich gezwungen, anzuerkennen, daß die
unterschlaͤchtigen Raͤder, bei einer Menge von Umstaͤnden,
einzig und allein mit Erfolg und Vortheil angewendet werden koͤnnen.
Da also die Vortheile der unterschlaͤchtigen Raͤder klar erwiesen sind,
und da diese Raͤder niemals, ausgenommen bei sehr kleinen Faͤllen,
mehr als 3/10 der Quantitaͤt der Wirkung, die man ihnen vertraut, und oft
selbst, bei der gewoͤhnlichen Stellung der Schuzbretter und Laͤufe,
nicht mehr als 1/4 oder 1/6 dieser Quantitaͤt zuruͤkgeben, so muß man
jene Untersuchungen als aͤußerst nuͤzlich anerkennen, welche von
verschiedenen Gelehrten, namentlich von Parent, Deparcieux,
Smeaton, Borda, Bossut, von Chevalier Morosi
etc. in der Absicht angestellt wurden, theils die Theorie derselben
aufzuklaͤren, theils Vervollkommnungen oder nuͤzliche Aenderungen in
ihrem Baue zu erfinden.
Diese Verbesserungen bestehen, wie man weiß, vorzuͤglich darin, 1) den
Raͤdern wenigstens 36 Eimer oder Schaufeln zu geben; 2) diese Eimer unter
einem Winkel von 15 bis 30° auf die verschiedenen Halbdurchmesser zu neigen;
3) diese Eimer so tief als moͤglich ins Wasser, zu 1/4 oder 1/3 ihrer
Hoͤhe, zu tauchen; 4) endlich an jedem ihrer senkrechten Enden Bandleisten
von ungefaͤhr 2 bis 3 Zoll Vorsprung anzubringen.
Einige Schriftsteller haben auch vorgeschlagen, etwas der Quere nach concave
Schaufeln anzuwenden; andere haben den unterschlaͤchtigen Raͤdern die
Form von Eimer-Raͤdern gegeben, indem sie die Schaufeln brachen. Fabre schrieb vor, eine Schwelle und eine Erweiterung am Laufe unter der
Achse des Rades anzubringen, um dadurch den Ausfluß des Wassers zu erleichtern, und
seine impulsive Wirkung zu vermehren; endlich hat man seit einiger Zeit
vorgeschlagen, den Waͤnden des Schuzbrettes die Form des Wasserfadens zu
geben, und dasselbe soviel moͤglich unter das Rad zu neigen, um die
Laͤnge des Laufes, den das Wasser durchfließt, und folglich auch den Verlust
an Geschwindigkeit zu vermindern, den es von Seite seiner Waͤnde erleidet.
Aber diese verschiedenen Mittel, außer dem lezteren, und jenem, welches von Morosi vorgeschlagen wurde, haben nie zu, fuͤr die
Praxis bedeutenden Vermehrungen der Wirkung, gefuͤhrt; was diese betrifft, so
ist es leicht, sie zu schaͤzen, und lezterer die Graͤnze ihres
respectiven Nuzens anzuweisen.
Man sieht sogleich, daß die vortheilhafteste Wirkung, die man erhalten kann, wenn man
das Schuzbrett vorwaͤrts neigt, und seinen Seitenwaͤnden die Form des
Wasserfadens gibt, diese ist, daß die Geschwindigkeit des Wassers beim Austritte aus
dem Behaͤlter und beim Eintreten in das Rad sichtbar dieselbe ist, so daß die
lebendige Kraft, oder die Quantitaͤt der Wirkung des Falles, nicht
geaͤndert wird: bei diesem Stande der Dinge, wird die Quantitaͤt der
durch das Eimer-Rad gelieferten Wirkung, statt nur 1/4 oder 1/5 jener des Falles zu
seyn, soviel man weiß, 3/10 betragen, was ohne Zweifel eine große Vermehrung der
Wirkung ist. Im zweiten Falle geht es aus den directen Erfahrungen des Hrn. Christian (Mecanique industrielle
T. I. p. 270 u. f.) hervor, daß die Vermehrung des Drukes, die durch die
Seiten-Leisten, Morosis entspringt, sich nur zu einem
oder zu zwei Zehnteln des Drukes, der auf die gewoͤhnlichen Schaufeln
ausgeuͤbt wird, erhebt; wenigstens dann, wann diese Schaufeln unbeweglich und
in einem Laufe eingeschlossen sind. Es ist selbst zweifelhaft, daß diese Vermehrung
bei wohl gebauten Raͤdern, die wenig Spiel im Laufe haben, so viel
betraͤgt, besonders wenn man, statt sie als unbeweglich anzunehmen, sie als
in Bewegung befindlich betrachtet. Es hieße sehr viel zugeben, wenn man
annaͤhme, daß die Leisten des Chev. Morosi das
Maximum der Wirkung der Schaufel-Raͤder um 0,2 ihres Werthes vermehren
koͤnnten; und da diese leztere geringer ist, als 0,3 der Quantitaͤt
der ganzen Wirkung, die das Wasser beim Austritte aus dem Laufe besizt, so sieht man, daß die Wirkung
der Leisten den Raͤdern hoͤchstens 0,36 dieser Quantitaͤt
verschaffen wird.
Wenn man jezt, statt die uͤbertragene Wirkung mit jener zu vergleichen, welche
das Wasser wirklich besizt, sie mit denjenigen vergleichen wollte, welche dem ganzen
Falle des Wassers von seinem Niveau an in dem Behaͤlter bis zum unteren Ende
des Rades zukommt, eine Quantitaͤt der Wirkung, die wahrhaft von der Art ist,
daß man sie in der Praxis beachten muß, so wuͤrde man wahrscheinlich finden,
daß sie, in den meisten Faͤllen, hoͤchstens 0,32 oder 0,33 ist.
Bei dieser Unvollkommenheit der senkrechten unterschlaͤchtigen Raͤder,
und gemaͤß den wohl bekannten Vortheilen, die ihnen auf der anderen Seite
zukommen, und woruͤber schon oben gesprochen wurde, suchte ich, indem ich die
vorzuͤglichsten Verbesserungen, die bei diesen Raͤdern bereits
angebracht wurden, benuͤzte, die Form derselben in der Art
abzuaͤndern, daß sie faͤhig wuͤrden, eine nuzbare Wirkung
hervorzubringen, welche sich mehr dem absoluten Maximum naͤherte, und sich
kaum von dem der besseren gebraͤuchlichen Raͤder entfernte, und dieses
zwar ohne sie ihrer ausgezeichneten Eigenschaft einer großen Schnelligkeit zu
berauben. Die ganze Frage besteht, wie man nach dem Principe der lebendigen
Kraͤfte weiß, darin, es so einzurichten, daß das Wasser, indem es keinen Stoß
bei seinem Eintritte in das Rad ausuͤbt, dasselbe gleichfalls
verlaͤßt, ohne merkliche Geschwindigkeit zu behalten.
Indem ich dieß uͤberlegte, schien es mir, daß man dieser doppelten Aufgabe
dadurch Genuͤge leisten koͤnne, wenn man die geraden Schaufeln der
gewoͤhnlichen Raͤder durch krumme oder cylindrische ersezen
wuͤrde, welche ihre Concavitaͤt dem Strome darbieten, und deren
Elemente, vom ersten an, welches sich an jenen des aͤußeren Umfanges des
Rades als Tangente anschließen wuͤrde, immer weniger und weniger gegen den
Halbmesser geneigt waͤren, und also eine krumme oder fortwaͤhrende
Oberflaͤche bilden wuͤrden. Es ist einleuchtend, daß das Wasser,
angelangt auf diesen Krummen, in einer fast tangentiellen Richtung mit ihrem ersten
Elemente, dort, ohne dieselben zu stoßen, sich bis zu einer Hoͤhe erheben
wird, welche der relativen Geschwindigkeit, die dasselbe besizt, zukommt, und dann
hinabsteigen wird, indem es von Neuem, aber in entgegengesezter Richtung, der
Bewegung des Rades, eine relative Geschwindigkeit erlangt, die jener gleich ist, welche es beim
Aufsteigen hatte. Wenn man nun die absolute Geschwindigkeit des Wassers beim
Austritte aus dem Rade gleich Null sezt; so findet man, daß die Bedingungen der
Aufgabe alle erfuͤllt seyn werden, indem der Umfang dieses Rades die mittlere
Geschwindigkeit des Laufes erhaͤlt, mithin eine Geschwindigkeit, die jener
gleich kommt, welche den gewoͤhnlichen Schaufelraͤdern zur Erzeugung
des Maximum der Wirkung zukommt; daraus folgt, daß die Raͤder mit krummen
Schaufeln, von welchen hier die Rede ist, außer dem Vortheile, daß sie die
moͤglich groͤßte Wirkung hervorbringen, auch noch den darbieten, daß
sie den gewoͤhnlichen Raͤdern ohne einige Veraͤnderungen
unmittelbar substituirt werden koͤnnen.
Wenn man Sorge traͤgt, das Schuzbrett so anzulegen, wie oben gesagt wurde, und
auf der anderen Seite einen Vorsprung und eine Erweiterung am Laufe dort, wo die
Krummen das Wasser auszuleeren anfangen, anzubringen, um die Ausleerungen derselben
zu erleichtern; wenn man endlich Leisten an jeder Seite der krummen Eimer nach
Morosis Methode anbringt, oder, was mehr ausrichtet, diese Eimer zwischen zwei
kreisfoͤrmigen Flaͤchen einschließt, wie man bei den
Eimer-Raͤdern es thut, (Flaͤchen, denen die Theorie uͤbrigens
nur eine Breite gibt, die 1/4 der Hoͤhe des Falles betraͤgt); so sieht
man, daß mittelst aller dieser Vorrichtungen das neue Rad nothwendig sehr
vortheilhafte Ergebnisse, welche die der ersten Verbesserungen uͤbertreffen,
geben muͤsse.
Der Gedanke, krumme Schaufeln statt der geraden des alten Systemes anzuwenden,
scheint so natuͤrlich und einfach, daß man glauben muß, er sey mehr als einer
Person eingefallen; auch masse ich mir nicht an, demselben großes Verdienst
beizulegen; allein, so wie die einfachsten Ideen oft mit den meisten Schwierigkeiten
zu kaͤmpfen haben, bis sie angenommen werden, und den Praktikern das mindeste
Vertrauen einfloͤßen, so wollte ich mich nicht an rein theoretische
Entwuͤrfe halten. Da mir uͤberdieß nicht unbekannt war, daß gewisse
Schriftsteller die Nuͤzlichkeit der Anwendung der rationellen Mechanik auf
die Maschinen in Zweifel gezogen haben, hielt ich es fuͤr nuͤzlich,
eine Reihe von Versuchen an einem Modelle von Raͤdern mit krummen Schaufeln
anzustellen, sowohl um durch die That die Geseze oder Formeln zu bestaͤtigen,
welche aus dem Principe der lebendigen Kraͤfte sich herleiten lassen, einem
Principe, das heute zu
Tage allgemein von den Geometern angenommen ist, als auch um die bestaͤndigen
Coefficienten zu entdeken, welche diese Formeln vervielfachen muͤssen, damit
sie unmittelbar fuͤr die Praxis anwendbar werden.
Man wird sehen, daß diese Formeln so genau bewiesen sind, als man es von Versuchen
dieser Art hoffen kann, und daß der Coefficient, worauf sich dieselben in den
verschiedenen Faͤllen beziehen, zwischen den Zahlen 0,60 und 0,76,
fuͤr das Modell des Rades bleibt, womit man die Versuche anstellte. Da ich
uͤberdieß von hier ausging, und dasjenige bedachte, was im Großen zutreffen
muß, wenn man der Oeffnung des Schuzbrettes und dem Gefaͤlle des Laufes die
gehoͤrigen Dimensionen gibt, so konnte ich approximativ schließen, daß die
Quantitaͤt der Wirkung, die durch ein Rad mit krummen Schaufeln, wirklich
geliefert wird, bei einem Falle von 0,80 bis 2,00 Meter nie geringer, als 0,6 seyn
kann, und oft 0,67 der Quantitaͤt der Wirkung, welche der ganzen Hoͤhe
des Wassers des Behaͤlters von seinem oberen Niveau an bis auf den
niedrigsten Punct des Rades gleich kommt; was ohne Widerrede die Ergebnisse
uͤbertrifft, welche man von den SeitenraͤdernEs sind Erfahrungen von Hrn. Christian (von dessen
Mécanique industrielle T. 1.)
uͤber ein Seitenrad vorhanden, aus denen hervorgeht, daß diese
Raͤder nur die Haͤlfte der Quantitaͤt der Wirkung, die
dem Falle zukommt, aͤußern: uͤberdieß war die dem Rade
gegebene Geschwindigkeit schwach und der Fall hinlaͤnglich stark. Zu
der naͤmlichen Folgerung leitet die Formel, welche H. Navies fuͤr Biest Art von Raͤdern
aufstellte. und selbst von den oberschlaͤchtigen Raͤdern, in dem einzelnen
Falle, wo es sich um einen kleinen Fall handelt, erhielt.
Folgende Abhandlung enthaͤlt die vorzuͤglichsten Ergebnisse der
Erfahrungen und Berechnungen, welche ich anstellte, um diese Schluͤsse und
mehrere andere zu ziehen; sie zerfaͤllt in drei Theile: der erste
enthaͤlt die Theorie und die allgemeine Bauart des neuen Rades nebst
Zugehoͤr; der zweite, die verschiedenen Versuche, welche man anstellte, um
die Geseze der Theorie und die mechanischen Wirkungen dieses Rades zu beweisen: der
dritte und vierte endlich beziehen sich auf die Geseze des Ausflußes des Wassers
quer uͤber das Schuzbrett und den Lauf des Apparates: Geseze, welche
nothwendig waren, um die Quantitaͤt der eigentlichen Wirkung des Wassers in
dem Augenblike, wo es
auf das Rad wirkt, kennen zu lernen, und daraus das Verhaͤltniß dieser
Quantitaͤt zu jener, welche durch das leztere im Falle des Maximum der
Wirkung geleistet wird, abzuleiten.
Ich halte es fuͤr noͤthig, im Voraus zu bemerken, daß die verschiedenen
Versuche, welche diese Abhandlung enthaͤlt, und, die numerischen
Berechnungen, welche sie benoͤthigen, gleichzeitig in den Monaten August und
September des Jahres 1824 gemacht wurden, und daß ich in diesem eben so zarten als
muͤhevollen Theile meiner Arbeit durch die Gefaͤlligkeit des Hrn.
Capitain's des Genie Lesbras, und durch seinen Eifer
fuͤr Foͤrderung der Wissenschaften unterstuͤzt wurde.
Erster Theil. Beschreibung und Theorie der
unterschlaͤchtigen senkrechten Raͤder mit krummen Schaufeln.
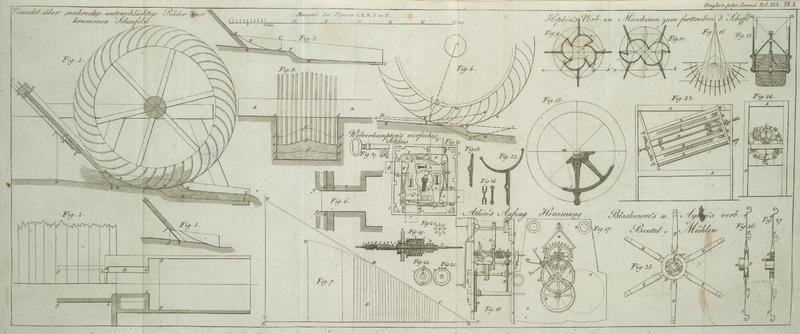
1. Die erste Figur stellt ein senkrechtes Rad mit krummen Schaufeln dar, welches so
gestellt ist, daß der Stoß des Wassers und der Verlust der Geschwindigkeit, welcher
gewoͤhnlich dann Statt findet, nachdem es auf das Rad gewirkt hat, soviel
moͤglich vermieden wird. Diese Schaufeln sind an ihren Enden in zwei
kreisfoͤrmige Ringe eingeschlossen, wie die Eimer-Raͤder, ohne jedoch,
wie diese einen Boden zu haben; sie koͤnnen aus schmalen Schienen
zusammengesezt seyn, wenn man sie aus Holz macht; sonst aber muͤssen sie aus
Einem Stuͤke bestehen, entweder aus Gußeisen oder aus Eisenblech, und dann
braucht man sie nicht in kreisfoͤrmige Buͤhnen einzulassen, indem man
dort Ohren oder Leisten anbringt, die auf diese Buͤhnen genagelt oder gebolzt
werden. In gewissen Faͤllen wird man es vorteilhafter finden, die Ringe zu
unterdruͤken, und sie durch Radschienen zu ersezen, wie dieß
gewoͤhnlich bei den unterschlaͤchtigen Raͤdern
gebraͤuchlich ist; die krummen Schaufeln muͤssen dann durch kleine
eiserne Klammern unterstuͤzt werden, deren unterer Theil uͤber der
Schiene angebracht ist, nachdem er dieselbe quer durchlaufen hat; der Rest der
Klammer, duͤnner und nach der Krummen gebogen, welche weiter unten untersucht
werden wird, muß in den Zwischenraͤumen mit kleinen Loͤchern
durchbohrt seyn, um die Naͤgel oder Bolzen aufzunehmen, welche bestimmt sind
die Oberstemme zu befestigen. In dem Falle, von welchem es sich hier handelt, wird
es uͤberdieß fuͤr die Wirkung nuͤzlich seyn, vorspringende
Leisten auf den Oberstemmen nach Morosis Systeme anzubringen:
diese Leisten koͤnnen 2–3 Zoll Uebersprung haben.
2) Hier nun die Haupt-Einrichtung des Laufes und des Schuzbrettes:
Der Lauf, BC, ist hier unter 1/10 geneigt in der
Absicht, dem Wasser den Verlust an Geschwindigkeit zu ersezen, der durch die Reibung
gegen die Waͤnde verursacht wird; seine Neigung kann ohne Nachtheil viel
kleiner seyn, wann die Wasserschichte dik, oder die Geschwindigkeit gering ist, wie
es meistens der Fall ist. Der Lauf muß so breit, oder, was noch besser ist, ein
wenig schmaͤler, als die Eimer des Rades seyn. In dieser Absicht muß man in
seinen Seitenwaͤnden kreisfoͤrmige Vertiefungen, D E C, (Fig. 1, 2 und 3.) anbringen, die
geeignet sind, die Ringe und einen Theil der Eimer des Rades aufzunehmen; es muß der
moͤglich kleinste Spielraum zwischen diesen Waͤnden und den Ringen
Statt finden; endlich muß man einen Vorsprung, E F, in
einer gewissen Entfernung von der Verticalen der Are des Rades anbringen, um dem
Wasser nach seinem Austritte aus den Krummen Ausfluß zu verschaffen: der Lauf muß
uͤberdieß soviel moͤglich in der Umgegend dieses Vorsprunges erweitert
seyn (Fig.
2.), um diesen Ausfluß desto mehr zu erleichtern. Was das Strebeholz, B O, betrifft, so ist es noͤthig, dasselbe so
vorwaͤrts zu neigen, daß es sich den Theilen des Rades naͤhert; und,
unter diesem Verhaͤltnisse, muß man auch das Schuzbrett, B R, außen anbringen, indem man es aus einer Platte von
starkem Bleche, oder aus einer Gußeisen-Platte, welche in einen Falz einpaßt, der an
den Baken des Laufes angebracht ist, verfertigt. Die Regierung desselben geschieht
mittelst einer Winde, oder auf jede andere Art.
Wir werden spaͤter auf diese verschiedenen Einrichtungen zuruͤk kommen,
wann wir durch Theorie und Versuche die einzelnen Daten der Frage aufgestellt haben
werden; fuͤr jezt genuͤgt es uns, eine allgemeine Idee des Apparates
gegeben zu haben.
3) Um die Theorie des Rades, um welches es sich hier handelt, fest zustellen, werden
wir bemerken, daß das Wasser, wann es aus der Schleuse tritt, eine Geschwindigkeit
annimmt, deren Richtung beinahe tangentiell mit dem Umkreise des Rades ist; so daß,
wenn man das erste Element der Krummen der Fluͤgel selbst als Tangente, oder
fast als Tangente zu diesem Umkreise annimmt, kein merklicher Stoß beim Eintritte des Wassers
in das Rad Statt haben wird. Das Wasser wird also nach der Laͤnge einer jeden
hinlaͤnglich verlaͤngerten Krummen mit einer relativen Geschwindigkeit
herabgleiten, welche dem Unterschiede seiner eigenen Geschwindigkeit und jener des
Rades gleich ist, und wird sich, indem es die Krumme druͤkt, zu einer
Hoͤhe erheben, die jener gleich ist, welche dieser Geschwindigkeit zugekommen
waͤre. Folglich, wenn der Aussprung, F, oder der
Vorsprung des Laufes so gestellt ist, daß der untere Rand der Krummen genau in dem
Augenblike dort ankommt, wo das Wasser seine groͤßte Erhebung erreicht, so
wird dasselbe wieder nach der Laͤnge der Krummen herabsteigen, indem es auf
dieselbe neuerdings druͤkt, und wird durch den unteren Theil mit einer
relativen Geschwindigkeit entfliehen, welche genau derjenigen gleich ist, die es bei
seinem Eintritte besaß, und zur Richtung jene des unteren Elementes dieser Krummen
hat. Was die absolute Geschwindigkeit des Wassers betrifft, so wird diese gleich
seyn dem Unterschiede zwischen seiner relativen Geschwindigkeit laͤngs der
Krummen und zwischen der Geschwindigkeit des Rades, weil man hier noch das lezte
Element der Krummen als merklich horizontal und tangentiell zu dem Umkreise dieses
Rades annehmen kann: da nun keine Kraft dort verloren ging, so muß diese absolute
Geschwindigkeit, wie man weiß, Null seyn.
Es sey nun, V, die Geschwindigkeit des Wassers dort, wo
es uͤber das Rad zu steigen beginnt; H, die
dieser Geschwindigkeit zukommende Hoͤhe: m, die
Masse Wassers, die in Einer Secunde fließt; endlich, v,
die unbekannte Geschwindigkeit, welche der Umkreis des Rades nehmen muß; so wird,
V – v, die relative Geschwindigkeit seyn,
womit sich das Wasser laͤngs der Krummen erhebt, und
((V – v)/2g)²
wird die Hoͤhe seyn, zu welcher es sich laͤngs
dieser Krummen erhebt: nach dem Vorhergehenden wird es von Neuem, wann es
laͤngs dieser naͤmlichen Krummen herabsteigt, die Geschwindigkeit, V – v, erlangen, und (V
– v) – v = V – 2v wird die absolute Geschwindigkeit beim Austritte aus
dem ade seyn; da diese Geschwindigkeit zur Hervorbringung des Maximum der Wirkung
null seyn muß, so wird V – 2v = 0, oder v = 1/2 V; d.h., das Rad muß die Haͤlfte der Geschwindigkeit
des Laufes erhalten; genau also, wie es bei den Raͤdern mit
gewoͤhnlichen Schaufeln der Fall ist. Ueberdieß ist es, nach dem Principe der
lebendigen Kraͤfte, einleuchtend, daß die Quantitaͤt der Wirkung, die
durch das Rad geliefert wird, der Theorie nach, gleich m g
H, d.h., derjenigen gleich seyn wird, welche das Wasser im Augenblike
seines Eintrittes in die Krummen besizt; was man uͤberdieß unmittelbar
beweisen kann, wie folgt:
4) Wenn die Bewegung des Rades als einfoͤrmig angenommen wird, und P, die bestaͤndig an seinem Umkreise in
Thaͤtigkeit gesezte Kraft ist, welche immer als gleich einem Gewichte
angenommen werden kann, das durch ein Seil gehoben wird, das uͤber eine
Trommel von demselben Durchmesser, wie das Rad, gerollt ist; so wird, P v, in der Einheit der Zeiten, die Quantitaͤt
der Wirkung seyn, welche dieser Kraft entspricht; die waͤhrend der
naͤmlichen Zeit durch den Fall verzehrte Quantitaͤt der Wirkung wird,
m g H; also wird m g H
– P v, die Quantitaͤt der ganzen Wirkung seyn, welche dem
Systeme mitgetheilt wird. Auf der anderen Seite ist die absolute Geschwindigkeit,
welche dem Wasser uͤbrig bleibt, nachdem es auf das Rad gewirkt hat,
gemaͤß dem Vorausgehenden, V – 2v: also ist die lebendige Kraft, welche am Ende der
fraglichen Zeit uͤbertragen wird, m, (V – 2v)²; und
folglich hat man, nach dem Principe der lebendigen Kraͤfte, m (V – 2v)² = 2 (mgH
–
Pv); woraus sich ergibt
Pv = mgH
– m ((V – 2v)/2)²;
und, weil V² = 2 gH
,
Pv = 2 m (V – v) v.
Dieß ist die Quantitaͤt der Wirkung, die dem Rade in der Einheit der Zeit
wirklich uͤbertragen wird, wann seine Bewegung zur Gleichfoͤrmigkeit
gekommen ist. Wenn man sie im Verhaͤltnisse zu v,
differenzirt, so findet man, wie oben, fuͤr die Geschwindigkeit, welche dem
Maximum der Wirkung entspricht, v = 1/2 V; und die Quantitaͤt der dem Rade gegebenen
Geschwindigkeit ist in diesem Falle
Pv = m V²/2 =
mgH;
d.h., sie ist gleich der Quantitaͤt der ganzen Wirkung
des Falles selbst.
Wenn man, D, den Ausfluß des Wassers in Einer Secunde dem
Volumen nach nennt, und bemerkt, daß g = 9,m 809; so erhaͤlt man, wie man weiß, m g = 100 Kil. D. nach
diesem werden obige Formeln, welche die Quantitaͤt der dem Rade
uͤbertragenen Wirkung ausdruͤken, fuͤr den Fall irgend einer
Geschwindigkeit v,
Pv = 2000D/9,809 (V – v) v = 203,8943 D (V – v) v;
und fuͤr den Fall des Maximum
Pv = 1000 DH.
Der Druk oder die Kraft, welche unter den naͤmlichen Umstaͤnden am Ende
des Halbmessers des Rades ausgeuͤbt wird, wird also respective seyn:
P = 203,8943 D (V – v) Kil.
P = 1000D
H/¹/₂V = 1000D V/g = 101, 9472 DV Kil.
Hieraus ersieht man, daß, der Theorie nach, 1) das Rad, von welchem die Rede ist,
eine doppelt so große Wirkung, als die gewoͤhnlichen
unterschlaͤchtigen Raͤder, welche zugleich der moͤglich
groͤßten aller Wirkungen gleich ist, hervorbringen wird; 2) daß der Druk oder
die Kraft, welche auf das Rad ausgeuͤbt wird, ebenfalls das Doppelte von
demjenigen ist, welches auf unterschlaͤchtige Raͤder fuͤr die
naͤmliche Geschwindigkeit ausgeuͤbt wird; ein kostbarer Vortheil in
allen Faͤllen, wo der zu besiegende Widerstand beim Abgange
betraͤchtlich ist; 3) daß die Geschwindigkeit des Rades, welche dem Maximum
der Wirkung entspricht, die Haͤlfte von der des Stromes ist, und folglich so
groß, wie bei den gewoͤhnlichen Schaufelraͤdern.
5) Verschiedene Umstaͤnde hindern, daß alles in der Praxis sich vollkommen so
verhalten kann; man muß daher dieselben untersuchen, ehe man weiter geht, sowohl um
ihren respectiven Einfluß auf die Ergebnisse kennen zu lernen, als auch um daraus
die Regeln fuͤr eine bessere Einrichtung, welche man den verschiedenen
Theilen des Systemes zu geben hat, abzuleiten.
Die vorausgehende Theorie sezt voraus, daß das Wasser in das Rad eintritt, ohne die
Krummen zu stoßen, und daß es aus demselben mit einer Geschwindigkeit austritt,
welche eine entgegengesezte Richtung, im Vergleiche derjenigen hat, welche der
Umkreis des Rades besizt: nun sind diese zwei Forderungen in der Praxis sehr schwer mit
voller Strenge zu erfuͤllen; man kann selbst sagen, daß sie sich
wechselseitig ausschließen.
Die leztere fordert, in der That, daß die Krumme der Eimer sich zum aͤußeren
Umkreise des Rades tangentiell verhalte, und um der anderen Genuͤge zu
leisten, muͤßte man ihr erstes Element in gewisser Quantitaͤt im
Verhaͤltnisse zum Umkreise neigen.
Betrachten wir z.B. (Fig. 4.) irgend einen Faden a b der
Wasser-Schichte, und nehmen wir uns vor zu suchen, welches die Richtung einer Ebene,
b c', seyn muß, damit diese Ebene keinen Stoß von
Seite des fluͤssigen Fadens, ab, erleide;
tragen wir hierzu die Geschwindigkeit, V, dieses Fadens
von, b, nach, c, in der
Richtung feiner Bewegung, und auf gleiche Weise die entsprechende Geschwindigkeit,
v, des Umkreises des Rades von, b, nach, d, auf die Tangente
in, b, zu diesem Umkreise; so wird die gerade Linie, cd, oder die mit ihr parallel laufende, b c', ganz einleuchtend die Richtung ausdruͤken,
welche man zur Erreichung des vorgestekten Zieles der Ebene geben muß. Man sieht
also, daß der Winkel, c'b d, der Ebene und des Umkreises
des Rades noch sehr beachtungswerth seyn muß, und daß er abaͤndert 1) nach
der eigenthuͤmlichen Stellung des fluͤßigen Fadens ab; 2) nach dem Verhaͤltnisse der
Geschwindigkeiten, v und V;
3) endlich nach der Groͤße des Umkreises des Rades.
6) Hinsichtlich der eigenthuͤmlichen Stellung des fluͤßigen Fadens, in
Bezug auf die Wasserschichte wovon er einen Theil ausmacht, sieht man, daß der
Winkel, c'b d. Null seyn muß fuͤr den unteren
Faden dieser Schichte, und daß er der moͤglich groͤßte seyn wird
fuͤr den oberen Faden in dem naͤmlichen Rade und fuͤr die
naͤmlichen Geschwindigkeiten, v und V; Sezen wir z.B., der Bogen, welcher durch die
Wasser-Flaͤche des Laufes umfaßt wird, sey 25°, was insbesondere
fuͤr den Fall paßt, wo diese Schichte eine Dichtigkeit von 25° und das
Rad 5 Meter im Durchmesser haͤtte; so wird dann der dem oberen Faden
entsprechende Winkel, c b d, auch 25° haben; und
wenn man fuͤr die Geschwindigkeit, v, eine
Geschwindigkeit annimmt, welche dem Maximum der Wirkung entspricht; so muß sie so
ziemlich (4) gleich seyn 1/2 V. Aus diesen respectiven
Werthen folgert man durch das Dreiek, b c d, daß der
Winkel, c'b d, der Ergaͤnzungs-Winkel von, b d c, ungefaͤhr 46''
betraͤgt; es muß sich also zwischen 0° und 46° der mittlere Neigungs-Winkel finden,
welcher sich fuͤr die Ebene, b c'; am besten
schikt. Wenn man 23° fuͤr diesen Winkel annimmt, wird man sich
wahrscheinlich nicht weit von der Neigung entfernen, welche das Minimum des Stoßes
gibt; wenigstens kann man sich geradehin versichern, daß der Verlust an
Kraͤften durch diesen Stoß aͤußerst gering ist im Verhaͤltnisse
zur ganzen lebendigen Kraft des Wassers.
Nennen wir, L, den Winkel, c'bd, welchen die Richtung, bd, des
fluͤßigen Fadens mit jener der stachen Schaufel, b
c', bildet, die in was immer fuͤr einer Stellung
angenommen wird; ferner, O, den Winkel, cbd, der durch diesen Faden mit dem
aͤußeren Umkreise des Rades gebildet wird, oder die Tangente, bd. Die verlorne lebendige Kraft kann als
verhaͤltnißmaͤßig zur Dichtigkeit der Wasserschichte angenommen
werden, welche unmittelbar auf die Ebene, b
c', stoͤßt, und zum Quadrate der Differenz der
Geschwindigkeiten, V und v,
nach der Senkrechten auf diese Ebene, d.h. [V sin. (L – B) – v sin.
B]² bemessen; wenn, m, die ganze Masse
des Fluidum's ist, welches in der Einheit der Zeit fließt, so wird also, im
Allgemeinen, diese Kraft kleiner seyn, als, m, [V. sin. (L – B) – v sin. B]² weil man dabei annimmt, daß
die ausgeflossene Wassermasse, m, auf die Ebene, b
c', nach der ganzen Hoͤhe stoͤßt, welche
sie im Laufe einnimmt; ein Umstand, der hoͤchstens fuͤr die Stellung
zutrifft, wo diese Ebene den Boden dieses Laufes beruͤhrt; wenn man nun, v und L, die oben
angegebenen Werthe gibt, und den Winkel, B oder cbd, von Null bis zu seiner Graͤnze, welche
25° ist, spielen laͤßt; so wird man finden, daß die Werthe der
vorhergehenden Formel zwischen 0 und 0,04. mV², begriffen bleiben. Der Verlust an Kraft durch die Wirkung des
Stoßes ist nicht einmahl das 4/100 der lebendigen Kraft, mV², welche die Masse des
anstroͤmenden Wassers besizt, und es ist wahrscheinlich, daß im mittleren
Durchschnitte derselbe nicht die Haͤlfte dieser Quantitaͤt
betraͤgt, immer unter den vor laͤusig angenommenen Voraussezungen,
welche unguͤnstig sind, da es in der Praxis selten sich zutragt, daß die
Wasserschichte, welche den Stoß ausuͤbt, das Rad unter einem Winkel von mehr
als 25° umfaßt.Man wird bemerken, daß, nach dem oben gefundenen Ausdruke, in gewissen
Stellungen der stachen Schaufel, b
c', der Druk des Wassers negativ werden,
d.h., in entgegengesezter Richtung von der Bewegung des Rades wirken kann;
wenn man nun dieses auf die krummen Schaufeln uͤbertraͤgt,
wird man leicht einsehen, daß es nur fuͤr einen sehr kleinen Theil
ihrer Ausdehnung statt findet; angefangen naͤhmlich von dem
aͤußeren Umkreise des Rades; die Wasserschichte, die auf diesen Theil
stoͤßt, wird also nicht nur ein sehr kleiner Bruch der ganzen in den
Lauf gedrungenen Wasserschichte seyn, so daß der normale Druk
aͤußerst schwach seyn wird, sondern es wird auch der Arm des Hebels
dieses Drukes, im Verhaͤltnisse zum Mittelpuncte des Rades viel
kleiner seyn, als der Radius, welcher den Arm des Hebels fuͤr den
Total-Druk, oder, fuͤr die auf dieses Rad ausgeuͤbte Kraft
vorstellt. Dieser Druk ist also, fuͤr die Praxis, leicht zu
uͤbergehen.
Bei der
gegenwaͤrtigen Unvollkommenheit der Hydraulik wuͤrde es, wie ich
glaube, sehr schwierig seyn, den Verlust an lebendiger Kraft durch den Stoß in der
Untersuchung, die uns beschaͤftigt, mit Genauigkeit zu bestimmen; die
vorausgehenden Betrachtungen koͤnnen hinreichen, um, im Allgemeinen, die
Graͤnzen zu bezeichnen, und sich uͤber die Wirkungen zu vergewissern,
welche man in vorgehender Theorie dem Stoße anzuweisen versuchte.
7. Ueberdieß scheint es nicht nothwendig, fuͤr den Fall krummer Schaufeln, das
erste Element dieser Krummen auf den Umkreis, des Rades so viel zu neigen, als es
die vorlaͤufig angestellten Betrachtungen uͤber die geraden Schaufeln
anzuzeigen scheinen, und statt 23° Neigung kann man ohne Gefahr ihnen viel
weniger, z.B. 10 bis 15° geben. Man merkt in der That, daß, da die
Wasserschichte, welche auf die krumme Schaufel stoͤßt, eine gewisse
Hoͤhe hat, nicht nur das erste Element der Krummen einen Stoß erleidet,
sondern mehrere nach einander folgende Elemente; nun sind diese Elemente mehr und
mehr auf den Umkreis des Rades geneigt, so daß das Wasser nothwendig auf eines
trifft, wofuͤr der Stoß Null ist.
Wenn man diese leztere Einrichtung fuͤr die Krummen annimmt, sieht man, daß
nicht nur die lebendige Kraft, welche durch den Stoß des Wassers verloren geht, sehr
gering ist, sondern daß auch die relative Geschwindigkeit dieses Wassers beim
Austritte aus den Krummen eine Richtung haben wird, die, gemaͤß der Theorie,
wahrscheinlich die angemessenste seyn wird.
8. Die Form der Krummen der Schaufeln ist ganz gleichguͤltig, wie man weiß,
vorausgesezt, daß sie eine fortlaufende ist, und daß sie dem Strome ihre Concavitaͤt
darbiethet; dieß gilt aber nicht ebenso von ihrer Hoͤhe uͤber dem
aͤußeren Umfange des Rades, d.h. von der Breite der Ringe; diese Hoͤhe
muß groß genug seyn, damit das zufließende Wasser seine ganze relative
Geschwindigkeit verlieren koͤnne, indem es die Laͤnge der Krummen
wieder herabsteigt.
Wir haben gesehen, daß die Geschwindigkeit des Aufsteigens des Wassers uͤber
die Laͤnge der Krummen, V – v, war, und
daß es sich zu einer Hoͤhe
((V – v)/2g)²
erhob; sie ist also veraͤnderlich mit der
Geschwindigkeit, v, des Rades, und die moͤglich
groͤßte fuͤr den Fall, wo das Rad unbeweglich ist; da diese
Hoͤhe dann
V²/2g
ist, so sieht man, daß man der Krummen eine Hoͤhe geben
muͤßte, die jener des Falles gleich waͤre, wenn man die ganze
Geschwindigkeit des Wassers beim Austritte aus dem Rade gewinnen wollte; allein da
diese Dimension der Schaufeln oft uͤbermaͤßig und unausfuͤhrbar
waͤre, und da man uͤberdieß ohne großen Nachtheil einen Theil der
Wirkung des Falles in dem Augenblike, um den es sich handelt, aufopfern kann, so
halten wir es in den meisten Fallen genuͤgend, den Krummen nur die
Hoͤhe zu geben, welche der Geschwindigkeit, v =
1/2 V, des Maximum der Wirkung, entspricht.
Obiger Ausdruk fuͤr diese Hoͤhe wird also
1/4 V²/2g'
d.h. sie ist genau ein Viertel des ganzen Falles. Fuͤr
die Faͤlle uͤber 2 Meter wird man es oft fuͤr vortheilhaft
finden, sich an dieses Verhaͤltniß zu halten, waͤhrend man sie
fuͤr viel kleinere Faͤlle ohne Nachtheil vergroͤßern kann,
indem man sie z.B. auf die Haͤlfte, oder ein Drittel der ganzen Hoͤhe
des Falles bringt. Man muß daher in allen Faͤllen uͤber die Bauart,
welche man anzubringen sich vornimmt, und nach der Beschaffenheit der Materialien,
die man dazu verwenden will, in's Reine kommen, ohne zu vergessen, daß immer ein
Vortheil mit der Vergroͤßerung der Krummen oder der Ringe, die sie enthalten,
verbunden ist; denn außerdem, daß es sich in der Praxis oft zutraͤgt, daß die
Geschwindigkeit der Raͤder sich mehr oder minder von jener entfernt, welche
dem Maximum der Wirkung entspricht, so hat man noch zu fuͤrchten, daß wenn
man die Hoͤhe der Krummen beschraͤnkt, man die Stoßkraft des Wassers
beim Austritte aus dem Rade vermindert. Wenn man uͤberdieß eine solche
Einrichtung trifft, daß in dem Augenblike, wo sich das Wasser uͤber die
Krummen erhebt, seine Richtung beinahe senkrecht mit der Richtung der Bewegung des
Rades ist; so wird der Verlust an Wirkung, der daraus entsteht, daß das Wasser die
Krummen verlaͤßt, wenig zu bedeuten haben, weil es dann aufhoͤrt auf
dieselben zu wirken, und im Zuruͤkfallen, neuerdings durch sein Gewicht und
durch seine erlangte Geschwindigkeit, auf das untere Wasser und die Krummen wirken
wird.
9. Nach allen diesen Betrachtungen, und zur Erleichterung der Ausfuͤhrung,
haben wir uns auf folgende Zeichnung der Krummen beschraͤnkt: wenn man irgend
einen Halbmesser, Ab (Fig. 4.) des Rades
gezogen, und die Breite, b
b', der Ringe, welche die Schaufeln einschließen
muͤssen, bestimmt hat, eine Breite, welche nie unter einem Viertel der
Total-Hoͤhe des Falles seyn duͤrfte; so fuͤhrt man von dem
Puncte, b, des aͤußeren Umkreises eine gerade
Linie, bo, die ungefaͤhr unter 10°
auf den Halbmesser, Ab, geneigt ist, gegen das
Schuzbrett, d.h. beinahe 1/6; wenn man ferner einen Punct, o, als Mittelpunct nimmt, welcher etwas uͤber dem inneren Umkreise
des Ringes liegt, z.B. um 1/7 oder 1/8 seiner Breite; so beschreibt man, mit der
Entfernung, bo, als Halbmesser, den Bogen des
Kreises, bm, der auf beiden Seiten sich am Ringe
endet; diesen Bogen wird man fuͤr die krummen Schaufeln des Rades nehmen
koͤnnen.
Was die Entfernung dieser Schaufeln betrifft, so steht sie im Verhaͤltnisse
mit dem Durchmesser des Rades, und kann sich nach den naͤhmlichen
Grundsaͤzen, wie fuͤr die gewoͤhnlichen
unterschlaͤchtigen Raͤder, richten; also wird man fuͤr
Raͤder, die 4 bis 5 Meter im Durchmesser halten, ohne Gefahr eine Zahl von 36
bis 40 Schaufeln anwenden koͤnnen.
10. Es bleibt uns noch uͤbrig, zu untersuchen, welche Form und Stellung man
dem Laufe und dem Vor- oder Aus-Sprunge, der sie beendigt, geben muͤsse,
damit die uͤbrigen Forderungen der Theorie auf die moͤglich beste
Weise erfuͤllt werden.
Die Betrachtungen, auf welche wir uns bisher gestuͤzt haben, sezen in der That
voraus, daß das Wasser den Krummen nicht ehe, als bis zu dem Augenblike selbst
entflieht, wo das untere Ende des Elementes derselben am niedrigsten Puncte des
Rades, und folglich des Falles, angekommen ist, denn, wenn es viel fruͤher
oder spaͤter entfliehen wuͤrde, so begreift, man, daß die ganze
Wirkung des Falles unnuͤz waͤre, und daß man den Theil dieses Falles
verloren haͤtte, welcher der Differenz des Niveaus zwischen dem Puncte, wo
das Wasser zu fließen anfaͤngt, und dem niedrigsten Puncte des Rades
entspricht.
Rufen wir uns zuruͤk (8), daß das Wasser sich in den Krummen zu einer
Hoͤhe erhebt, die im Allgemeinen
((V – v)/2g)²
ist; nun ist aber die Zeit, welche es brauchen wird, um bis zu
dieser naͤhmlichen Hoͤhe zu steigen, nach den bekannten Formeln:
(V – v)/g:
folglich ist der wirklich durch das Rad, waͤhrend
dieses naͤhmlichen Zeitraumes beschriebene Raum
v . (V – v)/g.
Man steht, nach diesem Ausdruke, daß dieser Raum Null oder sehr klein seyn wird
fuͤr die Geschwindigkeiten, v = o, v = V, des Rades; und der
moͤglich groͤßte fuͤr die Geschwindigkeit, v = 1/2 V, die genau dem
Maximum der theoretischen Wirkung des Rades entspricht;
v . (V–v)/g wird also 1/2 V²/g:
der Raum mithin, welchen der Umkreis des Rades
durchlaͤuft, waͤhrend das Wasser zu seiner ganzen Hoͤhe
laͤngs der Krummen sich erhebt, ist hoͤchstens die Haͤlfte der
ganzen Hoͤhe des Falles, und folglich wird ein anderer gleicher Raum durch
das Rad beschrieben, bevor jede Krumme ganz ihr Wasser verloren hat.
11. Es sey jezt, A, (Fig. 4.) ein Rad mit
krummen Schaufeln, dessen Lauf, BC, ich unter 1/10
geneigt annehme; es sey, DE, der obere Faden der
Wasserschichte, die auf das Rad wirken muß, waͤhrend, H, immer die Hoͤhe ist, welche der effectiven Geschwindigkeit des
Wassers im Laufe zukoͤmmt, und, E, der Punct oder
der obere Faden, welcher dem Umkreise des Rades begegnet; so muß man, nach dem
Vorausgehenden, die Laͤnge H/2 auf diesem
Umkreise von, E nach F,
ziehen, um den Punct, F, zu haben, wo das Wasser von dem
Rade abzugleiten anfaͤngt. Aber der obere Faden, DE, ist nicht allein; er haͤngt mit mehreren anderen zusammen,
welche, da sie ein wenig spaͤter in's Rad eintreten, kurz nach dem ersten aus
demselben treten, d.h., jenseits des Punctes, F, wenn
uͤberdieß diese verschiedenen fluͤßigen Faden nicht wechselseitig auf
sich Einfluß haͤtten, so daß sie fast im naͤhmlichen Augenblike aus
dem Rade treten. Wahrscheinlich wird man sich nicht viel von der Wirklichkeit
entfernen, wenn man den Austritts-Punct, F, nach dem
mittleren Faden, ab, der Wasserschichte des
Laufes, statt des oberen Fadens, DE, bestimmt.
Es ist einleuchtend, daß man an dem also bestimmten Puncte, F, den Vorsprung oder Aussprung des Laufes anbringen muß, um den Abfluß
des Wassers zu erleichtern, sobald es aus dem Rade zu treten beginnt; man kann in
dem Grunde des unteren Canales, HT, (Fig. 1, 3 und 4.) mittelst
einer geraden sehr geneigten Linie, oder durch eine Krumme, FH, anpassen, die zu diesem Grunde taugent ist. Es
wird auch vortheilhaft seyn, die Baken des Laufes im Puncte, F, zu endigen, um dem Wasser zu verstatten, sich unmittelbar nach der
ganzen Breite des Ausganges auszubreiten, welchen der untere Canal darbiethet, oder,
wenn dieß durch die Beschaffenheit der schon angebrachten Einrichtungen
unmoͤglich ist, so muß man, von der Stelle angefangen, wo es die Figuren 2 und
6.
andeuten, denselben erweitern.
Was die Hoͤhe des Vorsprunges, F, uͤber dem
Grunde des unteren Canales betrifft, so bezieht sie sich auf die
eigenthuͤmliche Leitung des Wassers in diesem Canale; und es laͤßt
sich in diesem Bezuge nichts besonderes vorschreiben, außer, daß man ihm die
moͤglich mindeste Erhoͤhung geben muß, um die Hoͤhe des Falles
nicht zu sehr zu vermindern. Uebrigens gelten die Vorschriften, welche man in dieser
Ruͤksicht geben koͤnnte, fuͤr alle Raͤder, aus welchen
das Wasser mit einer Geschwindigkeit entflieht, die Null oder fast Null ist, und man
wird bemerkt haben,
daß das Rad, welches uns beschaͤftigt, nicht im naͤhmlichen Grade, wie
die meisten anderen Raͤder, den Nachtheil hat, das Wasser nach hinten
aufzuheben oder zu stoßen, wenn es, wie man sagt, untergetaucht (noyé) ist, so daß es, in den meisten
Faͤllen, genuͤgen wird, den Aussprung, F,
in der Verlaͤngerung der oberen Oberflaͤche, KL, der Gewaͤsser des Canales fuͤr
den Ablauf anzubringen.
12. Jezt, um auf das zuruͤkzukommen, was uͤber die Bewegung des Wassers
in den Krummen gesagt wurde, wird man bemerken muͤssen, daß das Wasser, um
laͤngs der Krummen herabzusteigen, beinahe die naͤhmliche Zeit
brauchen wird, die es zum Hinaufsteigen noͤthig hat, so daß es nur
uͤber dem Puncte, F, (Fig. 4.) hinaus, welcher
oben in einer Entfernung, FG, die wahrscheinlich
etwas kleiner ist, als, EFo. H/2 bestimmt wurde,
vollkommen ausgeflossen seyn wird; nun trifft es sich aber in den meisten
Faͤllen, besonders wenn das Rad im Verhaͤltnisse zum Falle groß ist,
daß der Punct, G, sich nicht viel uͤber den
unteren Punct des Rades erheben wird, so daß ein sehr kleiner Theil der Wirkung
durch den Fall des Wassers außer den Krummen verloren geht, um so mehr, als der
groͤßere Theil dieses Wassers nahe am Puncte, F,
ausfließen wird.
In allen Faͤllen kann man den Nachtheil sehr vermindern, wenn man in einem
gewissen Verhaͤltnisse den unteren Punct des Rades unter den Grund, BF, des Laufes herabsteigen laͤßt, und
lezteren zur Aufnahme desselben kreisfoͤrmig aushoͤhlt; diese
Vorrichtung wird offenbar dazu dienen, den Punct, G, des
senkrechten Halbmessers des Rades anzunaͤhern, und vermindert sehr den
Verlust des Wassers im Laufe; daher empfehlen wir auch in der Praxis davon Gebrauch
zu machen. In der Mehrzahl der Faͤlle wird es genuͤgen, das Rad 2 bis
3 Zolle unter der Linie des Gefaͤlles des Laufes einzusenken, wie man in Fig. 5.
ausgedruͤkt findet.
Wir denken, daß, wenn man nach den verschiedenen Grundsaͤzen, die wir
erlaͤutert haben, verfaͤhrt, man sich nicht weit von den besseren
Einrichtungen entfernen wird, welche man den unterschlaͤchtigen
Raͤdern mit krummen Schaufeln geben muß; allein um uns nicht auf rein
theoretische Betrachtungen zu beschraͤnken, unternahmen wir eine Reihe von
Versuchen an einem Modelle im Kleinen, sowohl um die durch den Calcul angezeigten
Vortheile zu
wuͤrdigen und zu bestaͤtigen, als auch um verschiedene interessante
Fragen aufzuklaͤren, welche durch die Theorie nicht auf eine
genuͤgende und vollstaͤndige Weise geloͤset werden
koͤnnen, und auf welche zuruͤkzukommen wir also Gelegenheit haben
werden.
Zweiter Theil. Erfahrungen uͤber die
Wirkungen der senkrechten unterschlaͤchtigen Raͤder mit krummen
Schaufeln.
13. Das Rad, dessen wir uns zu diesen Versuchen bedienten, ist in Fig. 1. vorgestellt, und
war im Fuͤnftel-Maßstabe nach den vorlaͤufig entwikelten
Grundsaͤzen gebaut: sein Durchmesser, von außen genommen, betraͤgt 50
Centimeter; die krummen Schaufeln aus feinem Holze haben 2 bis 3 Millimeter Dike;
ihre Hoͤhe, oder die Breite der kreisfoͤrmigen Ringe, betraͤgt
ungefaͤhr 62 Millimeter und die Entfernung zwischen diesen Ringen oder die
horizontale Breite der krummen Schaufeln betraͤgt im mittleren Maße 76
Millimeter, und gleicht der Breite des Laufes nahe am Schuzbrette: es war ohne
Widerrede vorzuziehen, den Krummen eine uͤbermaͤßige Breite zu geben,
um versichert zu seyn, daß das Wasser, in keinem Falle, die Dike der Schienen oder
Ringe erreichte.
Die ganze Breite des Rades, mit Einschluß des Ringes, ist ungefaͤhr 103
Millimeter, waͤhrend die des Laufes am Vorsprunge 111 Millimeter
betraͤgt; der Spielraum war also ungefaͤhr 8 Millimeter fuͤr
die zwei Seiten des Rades; betrug aber unten nur 2 Millimeter. Im Allgemeinen ließ
das Rad, aus Nußbaum-Holz und ohne viele Sorgfalt verfertigt, genug Wasser durch
seine Seiten ausstießen, und drehte sich, wie man zu sagen pflegt, nicht rund: durch
die Feuchtigkeit und Trokenheit hatte es sich geworfen, und daher mußte man ihm viel
Spielraum im Laufe geben. Mit einem Worte, es ist sehr wahrscheinlich, daß, mit
Beobachtung des ganzen Verhaͤltnisses, die Raͤder im Großen mit mehr
Genauigkeit ausgefuͤhrt wuͤrden, und dieser Grund spricht zu Gunsten
der Ergebnisse aus unseren Versuchen; uͤbrigens betrug das Gewicht dieses
Rades ungefaͤhr 3,25 Pfund.
14. Hier nun die uͤbrigen vorzuͤglichen Einrichtungen, die wir
angebracht haben: das Wasser, welches dem Rade die Bewegung gibt, war in einem
Gefaͤße von ungefaͤhr 80 Cent. Breite und 30 Tiefe eingeschlossen, das
vorne offen war, um unmittelbar das Wasser eines kleinen Baches aufzunehmen, den es
gaͤnzlich verdaͤmmte; ein Theil der Wand, an der Seite des Rades, ist
vorwaͤrts geneigt, wie es unter Nr. 2. erklaͤrt wurde, und in Fig. 1. und
2.
dargestellt ist; und man hat an seinem unteren Theile eine Schleuse von der Breite
des Laufes, d.h. von ungefaͤhr 76 Millimeter, und von ungefaͤhr 37
Millimeter Hoͤhe, senkrecht im Grunde des Laufes gemessen, angebracht, dessen
Gefaͤlle zu 1/10, sich im Inneren des Gefaͤßes bis zu einer Entfernung
von ungefaͤhr 10 Centimeter verlaͤngert. Die Seitenraͤnder
dieser Schleuse sind so zugerundet, daß sie so viel moͤglich die
Zusammenziehung der fluͤssigen Ader vermeiden, und um sie zu schließen, ist
innenwendig ein erstes hoͤlzernes Schuzbrett, ab, (Fig.
1.) angebracht, welches etwas uͤber die Zurundungen der Schleuse
hinausgeht, und uͤberdieß eine Stange, ac,
traͤgt, um sie nach Belieben zu heben oder zu senken, wenn man dem Rade
Wasser geben will.
Da dieses Schuzbrett uͤbrigens fuͤr dieselbe Reihe von Versuchen oft
geoͤffnet und geschlossen werden mußte, so konnte es nicht dazu dienen, die
Oeffnung der Schleuse mit genuͤgender Genauigkeit zu bestimmen; man brachte
daher vorne ein anderes, BR, aus feinem Bleche an,
das sich in sehr engen Falzen schiebt, welche genau in der Verlaͤngerung der
aͤußeren Flaͤche des Ruͤkhaltes liegen, so daß dadurch kein
Verlust an Wasser entsteht. Da dieses Schuzbrett zur Regulirung der wahren Oeffnung
dient, so beruͤhrte man es nicht, außer wann es nothwendig war, es
fuͤr eine neue Reihe von Versuchen zu aͤndern; man trug Sorge, das
innere Schuzbrett hinlaͤnglich zu erheben, damit es auf keine Weise den Fluß
des Wassers stoͤren konnte. Uebrigens machten wir auf die uͤbrigen
Vortheile, welche mit dieser Einrichtung verbunden sind, schon (unter 2)
aufmerksam.
15, Um mit hinlaͤnglich strenger Genauigkeit die Oeffnung des aͤußeren
Schuzbrettes zu bestimmen, ließen wir uns kleine Lineale von Holz verfertigen,
welche zur Breite die verschiedenen anzubringenden Oeffnungen hatten; man traf alle
noͤthige Vorsicht, um sich zu versichern, daß sie nicht in dem Augenblike, wo
man sich ihrer bedienen mußte, betraͤchtlich abwichen; man befestigte dann
die eine ihrer beiden Flaͤchen am geneigten Grunde des Laufes, und senkte das
Schuzbrett, bis sein unteres Ende die andere Flaͤche beruͤhrte; man
ließ dann das Lineal nach allen Richtungen zwischen das Schuzbrett und den Lauf
gleiten, indem man es
genau in senkrechter Richtung hielt: es ist einleuchtend, daß die Dike des Lineals
genau die Schleusen-Oeffnung gab.
Was die Art, die Hoͤhe des Wassers im Gefaͤße zu bestimmen, betrifft,
so wandten wir anfaͤnglich einen Schwimmer an, welcher sich nach der
Laͤnge einer graduirten Stange auf und nieder schob; als aber dieser
Schwimmer gebrochen war, so sezte man an seine Stelle spaͤter das gerade Maß
der Wassertiefe, mit Huͤlfe eines Lineales von Kutsch, welches in Millimeter abgetheilt war: dieses Maß wurde
verschiedene Male in demselben Versuche genommen, um sich zu uͤberzeugen, daß
sich das Niveau nicht bedeutend geaͤndert habe.
16. Die Weise das Niveau zu bestimmen ist, wie man weiß, der zarteste und schwerste
Theil bei Versuchen dieser Art; sie erfordert viele Sorgfalt und Geduld. Da uns
uͤberdieß die mehr oder minder sinnreichen Mittel, welche von verschiedenen
Kunstverstaͤndigen angewendet werden, nicht zu Gebote standen; so
begnuͤgten wir uns auf der Seite des Gefaͤßes oder Behaͤlters
einen Kanal und ein Schuzbrett fuͤr den Abfluß anzubringen, dessen
Dimensionen dem ganzen Strome des Wassers, welches der Bach lieferte,
genuͤgten: da das kleine Schuzbrett des Rades auf angemessene Weise erhoben
war; so bestimmte man durch oͤfteres langes Versuchen die Oeffnung dieses
Abflusses so, daß man ein bestaͤndiges Niveau erhielt, welches der
eigentliche Gegenstand des anzustellenden Versuches erforderte.
Die Zeit wurde mittelst eines Zaͤhlers von Breguet
gemessen, welcher halbe Secunden gibt, und man erhielt die Quantitaͤt
Wassers, welche in einer Secunde floß, durch die Zeit, welche erforderlich war, ein
mehrere Male geeichtes Gefaͤß zu fuͤllen, das genau 184 Liter faßte.
Man hielt immer nur jene Versuche fuͤr gut, welche mehrmals wiederholt, nur
Differenzen von einer halben Secunde in der ganzen Dauer des Fließens gaben, und
ebenso ward es auch mit den uͤbrigen Arten von Versuchen, wovon in der Folge
Rechenschaft gegeben wird, gehalten.
17. Ehe wir weiter gehen, und die Anordnungen beschreiben, mittelst welcher man dahin
gelangte, genau die Quantitaͤten der Wirkung zu bestimmen, welche durch das
Rad unter verschiedenem Falle und bei verschiedenen Oeffnungen des Schuzbrettes
geliefert werden, ist es noͤthig einen merkwuͤrdigen Umstand anzufuͤhren: als
ich naͤmlich zum ersten Male das Wasser in den Lauf einlassen wollte, um die
Weise zu beobachten, wie sich der Ausfluß machte, war ich ganz uͤberrascht zu
sehen, daß statt daß es aus dem Schuzbrette in parallelen Faden austrat, wie man
gemaͤß der Sorgfalt erwarten durfte, womit man die inneren Waͤnde des
Laufes ausgeschweift hatte, sich das Wasser in einer sehr feinen Schichte von 10 bis
12° senkrechter Hoͤhe uͤber den Grund des Laufes erhob, indem
es so seine Seiten-Waͤnde verließ. Nachdem ich einige Augenblike uͤber
diese sonderbare Erscheinung nachgedacht hatte, erkannte ich bald, daß dieses einzig
davon herruͤhrte, daß die inneren Waͤnde des Gefaͤßes gegen den
Grund desselben geneigt waren, und mit diesem einen sehr spizigen Winkel an der
Seite, und einen anderen an der Schleuse bildeten, wodurch das Wasser mit
hinlaͤnglicher Schnelligkeit ankam, um die Schichte zusammenzuziehen, und
gezwungen wurde, sich im Laufe zu erheben.
In der Folge ließ ich zwei dreiekige Schienen verfertigen, die in, f g h, g'h' (Fig. 1. und 2.) vorgestellt
sind, und eine Dike von 27 Millimeter bei 27 Centimeter an der Basis hatten; sie
waren zu beiden Seiten des Schuzbrettes angebracht, so daß sie die Winkel, von denen
die Frage war, einfaßten, und gleichfalls die Verlaͤngerung des Laufes in dem
Gefaͤße bildeten, obwohl sie unter sich mehr entfernt waren, als die
Waͤnde dieses lezteren: die Wirkung hoͤrte bald auf, oder wurde so
wenig bemerkbar, daß sie mit dem Rade zu arbeiten, und die Wasserschichte, welche
dort eintritt, fast mit dem Grunde des Laufes parallel zu betrachten erlaubte; was
unerlaͤßlich ist, um den Stoß gegen die Krummen zu vermeiden.
18. Indem ich diese Einrichtung waͤhlte, fanden sich die Umstaͤnde des
Abflusses jenen aͤhnlich, die haͤufig in der Praxis vorkommen, wann
die Waͤnde des Laufes uͤber das Schuzbrett hinaus verlaͤngert
sind, indem sie so einen engen Kanal von Seite des Ruͤkhaltes bilden; aber,
außer dem, daß diese Einrichtung die Erscheinung des Abflusses complicirt, indem sie
von den gewoͤhnlichen Annahmen der Theorie abweicht, bietet sie auch noch den
viel groͤßeren Nachtheil dar, daß dem Wasser ein betraͤchtlicher Theil
der Geschwindigkeit, welche es dadurch erlangte, daß man dem Eintritts-Kanale
groͤßere Breite gab, hierdurch entzogen wird: denn nicht nur lassen die
Waͤnde dieses Kanales dem Wasser, das dort circulirt, einen um so
groͤßeren Widerstand fuͤhlen, je kleiner sein Abschnitt und je
betraͤchtlicher seine Laͤnge ist, sondern es findet auch eine leichte
Zusammenziehung beim Eintritte des Wassers in diesen Kanal Statt, wann es in ein
Beken einmuͤndet, dessen horizontaler Abschnitt weit staͤrker ist;
dieß traͤgt offenbar dazu bei, die Geschwindigkeit beim Austritte aus der
Schleuse zu vermindern.
Man haͤtte großen Theiles diese Nachtheile vermieden, wenn man die
Laͤnge des inneren Kanales verminderte, und uͤberdieß den ganzen
Winkel oder die Eke zwischen der geneigten Wand des Schuzbrettes und dem Grunde des
Laufes einfaßte. Man konnte sich z.B. begnuͤgen, (Fig. 5. und 6.) zwei
dreiekige Leisten, f g h, g'h' in diesem Winkel
anzubringen, deren senkrechte Flaͤchen, fg,
dem oberen Vorsprunge der Schleuse entsprochen haͤtten, wie man in Fig. 5. steht;
ihr Vorsprung, gh, im Inneren wuͤrde dann
auf 4 bis 5c zuruͤkgefuͤhrt worden seyn.
Ueberdieß waͤre es zwekmaͤßig gewesen, die Enden, g'h', der Leisten in die Verlaͤngerung der Baken
des Laufes zu sezen, und sie zuzurunden, um die Contraction zu vermeiden. Einige,
neulich angestellte, Versuche hatten uns wirklich belehrt, daß man durch diese
einfachen Vorrichtungen mit Vortheil seinen vorgesezten Zwek erreichen
wuͤrde, indem das Wasser aus dem Behaͤlter in einer sehr
regelmaͤßigen Schichte austritt, welche in Profil eine gerade parallele Linie
im Grunde des Laufes vorstellt. Daher muß man nie unterlassen, diese Vorrichtungen
in der Praxis anzuwenden, wenn man die Nachtheile vermeiden will, welche durch
geneigte Schuzbretter verursacht werden.
19. Da ich ferner nur fuͤr kurze Zeit uͤber den Bach verfuͤgen
konnte, wo das Rad angebracht war; da er seinen Zufluß nur durch das Wasser erhielt,
welches zufaͤlliger Weise bei einer hydraulischen Vorrichtung, die an dem
oberen Theile angebracht war, entwischte; so begnuͤgte ich mich durch ein
schleuniges Mittel einem Nachtheile vorgebeugt zu haben, welcher anfangs sehr groß
war; und ohne mich fuͤr den Augenblik mit der Aufsuchung passenderer Mittel
das Schuzbrett des Ruͤkhaltes in Ordnung zu bringen, aufzuhalten, unternahm
ich eine Reihe von Versuchen, die noͤthig waren, um die durch das Rad
gelieferte Quantitaͤt der Wirkung zu bestimmen, was ein wesentlicher
Gegenstand der Untersuchungen war, die man zur Absicht hatte; ich versparte
uͤbrigens auf eine andere Epoche von Versuchen die Wirkungen der Vorrichtung,
deren man sich bediente, genau zu bestimmen, d.h., den Verlust an Geschwindigkeit,
welcher fuͤr das Wasser dort entspringt, wo es auf das Rad wirkt.
20. Man weiß, daß, um die Quantitaͤt an Wirkung, die von einem hydraulischen
Rade geliefert wird, zu schaͤzen, das einfachste Mittel dieses ist, von
demselben ein Gewicht mit Huͤlfe eines Strikes oder Bindfadens heben zu
lassen, welcher uͤber eine Rolle geht und sich mit seinem anderen Ende
uͤber die Achse des Rades rollt: diese Quantitaͤt an Wirkung hat, in
der That, das Product des aufgehobenen Gewichtes, vermehrt durch den passiven
Widerstand, mit der Hoͤhe, zu welcher es in der Einheit der Zeit erhoben
wurde.
Die Erhoͤhung der Rolle uͤber das Rad betrug ungefaͤhr 8 Meter;
diese Rolle hatte selbst 9 Centimeter im Durchmesser, und befand sich fast senkrecht
uͤber der Achse des Rades, woruͤber sich der Faden von 2 bis 3
Millimeter Durchmesser aufrollte. Dieses Gewicht befand sich in einem kleinen Sake
von Tuch, den man vorlaͤufig gewogen hatte.
Vor allem mußte man den Widerstand, welcher der Luft und der Steife des Fadens, so
wie der Reibung der Zapfen zukommt, fuͤr die verschiedenen Geschwindigkeiten
des Rades approximativ bestimmen: man verschloß folglich die Wanne hermetisch, und
nachdem man nach und nach verschiedene Gewichte in den Sak gebracht hatte, erhob man
diesen zur moͤglich groͤßten Hoͤhe, indem man den Faden um die
Achse des Rades rollte, so daß das Gewicht beim Herabsteigen dieses Rad in der
naͤmlichen Richtung herumdrehte, als wenn es auf einfache Weise durch das
Wasser bewegt wuͤrde. Man ließ dann das Rad 10 ganze Umdrehungen machen,
damit es beinahe eine gleichfoͤrmige Bewegung unter der Wirkung des Gewichtes
erlangte; der Anfang und das Ende jeder Umdrehung wurden sehr genau durch einen
Zeiger am Zapfen der Achse angezeigt.
Dieses vorausgesezt, zaͤhlte man mehrmals die Zeit, welche das Rad brauchte,
um genau eine gewisse runde Zahl von Drehungen zu machen, die im Allgemeinen 200. 25
betrugen. Man entwarf sich hiernach eine Tabelle der verschiedenen
Geschwindigkeiten, welche das Rad bei den im Sake befindlichen Gewichten annahm;
wenn nun die Bewegung jedes Mal zur Einheit gekommen war, waren diese Gewichte genau
jene, welche ins Gleichgewicht sezten, oder alle vereinigten Widerstaͤnde des
Rades darstellten, wenn es leer geht.
Wann man dann das Rad mittelst des Wassers ein gewisses Gewicht aufheben ließ, trug
man Sorge, diesem Gewichte dasjenige beizufuͤgen, was, in der Tabelle, der
einfoͤrmigen Geschwindigkeit entsprach, welche dieses Rad genommen hatte, und
man erhielt so das ganze aufgehobene Gewicht, die Widerstaͤnde mit
einbegriffen.
Diese Methode, die von verschiedenen Maͤnnern angewendet wurde, ist doch noch
immer nicht in ganz mathemathischer Strenge genau genug; denn da das Rad eine Kraft
von Seite des Wassers erleidet, wann es durch dieses bewegt wird, und da der Sak
dann mehr sich belastet findet, als wenn er leer geht; so ist einerseits die
Spannung, und folglich die Steife des Fadens staͤrker, und auf der anderen
Seite ist der Druk und die Reibung uͤber den Rollen veraͤndert. Es
wuͤrde ohne Zweifel sehr schwierig seyn, auf diese lezteren Ursachen in den
Versuchen Ruͤksicht zu nehmen, welche sehr vervielfaͤltigt werden
muͤssen; aber gluͤklicher Weise gibt es Abziehungen und
Ergaͤnzungen, welche die Total-Summe der Widerstaͤnde in den
verschiedenen Faͤllen vermindern; eine Summe, welche uͤberdieß viel
schwaͤcher ist, als der Widerstand, der sich aus den Versuchen uͤber
das leere Rad ergab.
21. Um einen Begriff von der Weise zu geben, nach welcher wir bestaͤndig zu
Werke gingen, und um den Grad von Sorgfalt und Genauigkeit in den Versuchen
wuͤrdigen zu lassen, wollen wir das Detail von einigen derselben liefern, und
daraus die strenge Bestaͤtigung mehrerer interessanter Puncte der Theorie
herleiten. Wir werden z.B. eine Reihe von Versuchen waͤhlen, die sehr weit
getrieben wurden, um die Geseze kennen zu lernen, nach welchen die Wirkungen der
Raͤder mit krummen Schaufeln vor sich gehen, wann man sie verschiedene
Geschwindigkeiten unter verschiedenen Lasten annehmen laͤßt. Bei allen diesen
Versuchen wurde die Oeffnung des aͤußeren Schuzbrettes zu 3 Centimetern
erhalten, und die Hoͤhe des Niveaus des Wassers in dem Behaͤlter
uͤber dem Aussprunge dieses Schuzbrettes entfernte sich nicht merklich von
234 Millimetern; der Aufwand an Wasser wurde fuͤr die Secunde zu 3,8942 Liter
nach wiederholten Versuchen befunden. Man versicherte sich uͤberdieß, daß
jede Umdrehung des Rades genau 0,m 2188 des Fadens entwikelte, d.h., daß das
Gegengewicht sich zu dieser Hoͤhe fuͤr jede Umdrehung des Rades erhob,
um dahin zu gelangen, hatte man unmittelbar die entsprechende Erhebung des Gewichtes
fuͤr genau 18 Umdrehungen des Rades bestimmt.
Nachdem die Sachen so vorgerichtet waren, begann man das Rad unbelastet gehen zu
lassen, und fand, daß es 25 Umdrehungen in 19'',5 machte; man brachte dann in den
Sak ein Gewicht von einem Kilogramme, das man nach und nach bei jedem Versuche bis
auf ungefaͤhr 5 Kilogr. erhoͤhte, und uͤber welches hinaus. das
Rad seine regelmaͤßige und einfoͤrmige Bewegung verlor. Diese Zahl
haͤtte ohne Zweifel weiter hinausgesezt werden koͤnnen, wenn das Rad
gut gebaut gewesen waͤre; allein, so wie schon bemerkt wurde, das Rad war
nicht genau centrirt, und drehte sich nicht vollkommen in die Runde. Bei jedem
Versuche ließ man uͤbrigens das Rad 6 bis 8 Umdrehungen machen, ehe man die
Zeit am Chronometer zaͤhlte; man ließ dann das Rad 25 neue Umdrehungen
machen, um mit großer Annaͤherung die Zahl der Umdrehungen fuͤr Eine
Secunde, dann die Hoͤhe des Hinaufsteigens des Gewichtes, und zulezt die
Quantitaͤt der Wirkung des Rades, oder das Product dieser Hoͤhe durch
das mit den Widerstaͤnden, welche sich bei den Versuchen ohne Wasser ergaben,
vermehrte Gewicht zu erhalten. Folgende Tabelle zeigt die Reihe der verschiedenen
Daten des Versuches, und die Ergebnisse, die man daraus durch Calcul ableitete. Die
Zahlen der zweiten Columne wurden durch 3 oder 4 Versuche erhalten, die beinahe auf
eine halbe Secunde uͤbereinstimmten.
Tabelle der aufgehobenen Gewichte und der Quantitaͤten der
Wirkung, die vom Rade, bei einer Oeffnung des Schuz-Brettes auf 3 Centimeter und
einem Falle von 234 Millimeter geleistet wurden.
Textabbildung Bd. 19, S. 446
Nummern der Versuche; Zeit
fuͤr 25 Umdrehungen des Rades; Zahl der Umdrehungen in Einer Secunde;
Hoͤhe, zu welcher sich das Gewicht in Einer Secunde erhob; Gehobenes
Gewicht, mit Inbegriff jenes des Sakes; Gewicht, welches den
Widerstaͤnden das Gleichgewicht haͤlt; Total-Gewicht, welches vom
Rade gehoben wurde; Quantitaͤt der Wirkung, welche vom Rade geleistet
wurde
Beobachtungen.
22) Man steht, daß die Geschwindigkeiten und die Quantitaͤten der Wirkung, welche das Rad
liefert, einen sehr regelmaͤßigen Gang befolgen, obwohl die Werthe der Zahlen
bis auf die vierte Decimalstelle fortgesezt wurden. Um zu erfahren, ob die auf diese
Weise durch Erfahrungen gegebenen Geseze sich denen annaͤherten, welche die
Theorie gab, brauchten wir dazu das sehr einfache und schnelle Mittel der Krummen,
und da nach den n°. 4. aufgestellten Formeln die
Druke oder Kraͤfte, P, die auf das Rad wirkten,
einem Geseze folgen, welches viel leichter zu pruͤfen ist, als die
Quantitaͤten der Wirkung, die ihm entsprechen, so nahmen wir diese Druke,
oder vielmehr die aufgehobenen Gewichte, die ihnen proportionell sind, als die
Ordinaten der Krummen, und als Abscissen die Geschwindigkeiten, oder vielmehr die
Zahlen der Umdrehungen des Rades waͤhrend der Einheit der Zeit.
Um eine hinlaͤngliche Annaͤherung zu erhalten, stellte man jedes
Hundertel der Umdrehung des Rades und jedes Zehntel des Kilogramms des gehobenen
Gewichtes, durch zwei Mit. dar; so daß man leicht die Tausendtheile der Umdrehung,
und die Hundertel des Kilogrammes erhalten konnte: da die Zahlen der einen wie der
anderen unmittelbar durch die Columnen 3 und 7 der Tabelle gegeben waren, war es
leicht die Krumme des Gewichtes, BMC, (Fig. 7.) zu
construiren, welche dort nur im halben Maßstabe vorgestellt ist.
Diese Krumme unterscheidet sich nicht merklich von einer geraden Linie, außer von der
Ordinate angefangen, welche dem Versuche n°. 31.
angehoͤrt; im ganzen uͤbrigen Reste ihres Laufes betragen die
Differenzen, als mehr oder weniger, nicht uͤber 1/2 Millimeter, was nach dem
Maßstabe, 25 Grammen gibt: da diese Differenzen nicht das Hundertel der
entsprechenden Gewichte betragen, so muß man sie einzig den unausweichlichen
Irrthuͤmern der Beobachtungen zuschreiben, und in der That, um sie ganz
verschwinden zu machen, reicht es hin, die in der zweiten Columne der Tabelle
eingetragenen Zahlen nur um eine Viertel-Secunde zu aͤndern, was ganz außer
den Werthen liegt, welche durch das gebrauchte Instrument sich ergaben. –
23. Da die dargestellte Theorie (n°. 4.), um die
Druke, P, die den verschiedenen Geschwindigkeiten, v, des Rades entsprechen, zu berechnen, die Formel
P = 203, 8943 D (V – v) Kil. gibt;
so sieht man, daß das allgemeine Gesez, welches sie anzeigt,
auf eine gewisser
Massen strenge Art durch alle Versuche, welche zwischen n°. 1 und 3, derselbe Tabelle begriffen sind, sich
bestaͤtigt findet. Was die folgenden Versuche betrifft, deren Ergebnisse sich
zu bedeutend von diesem Geseze entfernen, als daß man die Differenzen
Irrthuͤmern in der Beobachtung zuschreiben koͤnnte, so erinnern wir
uns (8), daß die oben gegebene Formel nur in der Annahme aufgestellt wurde, daß die
Schaufeln des Rades eine hinlaͤngliche Hoͤhe haͤtten, um das
Wasser nicht oben entwischen zu lassen: diese Annahme wird aber, ungefaͤhr
vom 31ten Versuche an, nicht erfuͤllt.
Um dieß zu bestaͤtigen, wird man bemerken, daß die groͤßte
Hoͤhe, zu welcher sich das Wasser in den Krummen, indem es auf dieselben
druͤkt, erhebt, dort (13), 0m,062
ist, und daß die Geschwindigkeit 1m,1028,
die dieser Hoͤhe zukaͤme, nach den Art. 8. gegebenen Gruͤnden,
so groß oder groͤßer seyn muß, als die relative entsprechende Geschwindigkeit
des Wassers und Rades, die durch V – v, ausgedruͤkt ist. Wenn man nun annimmt, daß die
Geschwindigkeit des Wassers, in dem Augenblik, wo es in das Rad tritt, sich nicht
viel von jener unterscheidet, welche dem mittleren Falle 0m,234 – 0m, 015 = 0m,219 uͤber dem Mittel-Puncte der
Oeffnung der Schleuse (21), zukommt; eine Annahme, welche sehr wenig von der
Wirklichkeit abweichen kann; so wird V = 2m,0727, und V
– v = 1m
1028, woher v = 0m,9699 ; dieß ist dann, im wirklichen Falle, die Geschwindigkeit des
Rades, uͤber welche das Wasser zu wirken aufhoͤrt, wie es die Theorie
erfordert. Wenn uͤbrigens der Umkreis des Rades ungefaͤhr 1m,59 ist, so ist die Zahl von Umdrehungen,
welche dieser Geschwindigkeit entspricht, 0m,9699/1,59 = 0,61, eine Zahl, die beinahe dem Versuche 30 der Tabelle
entspricht.
24) Ueberdieß haben wir schon bemerklich gemacht, (13), daß die Excentricitaͤt
des Rades und seine schlechte Bauart andere Ursachen sind, welche veranlassen, daß,
fuͤr schwache Geschwindigkeiten, die Bewegung des Systemes regelmaͤßig
und gleichfoͤrmig zu seyn aufhoͤrt; die Erfahrung hat selbst gelehrt,
daß bei allen Arten von Raͤdern die Bewegung lange Zeit vor dem Termine
stokte, die ihm die Theorie anwies; dieser Umstand muß ebenfalls der
Unvollkommenheit der Raͤder in der Wirklichkeit zugeschrieben werden, die bei
kleinen Geschwindigkeiten großen Einfluß ausuͤbt.
Nach diesen verschiedenen Betrachtungen wird man also uͤberrascht seyn, daß
die Uebereinstimmung der Theorie und der Erfahrung sich fuͤr den Fall unserer
Vorrichtung so weit gehalten hat; aber man muß sie nicht dem Zufalle zuschreiben, da
sie sich auf dieselbe Weise in allen Reihen von Versuchen aussprach, wodurch wir
eine große Menge von Groͤßen bestimmt haben: oft differirten sogar die
Ordinaten der Krummen des Gewichtes nur auf eine voͤllig unbestimmbare Art
von denen einer geraden Linie. Daher muß man im Allgemeinen die Principien, von
denen wir ausgingen (4), um die Theorie des senkrechten Rades mit krummen Schaufeln
aufzustellen, als genau und mit der Erfahrung uͤbereinstimmend anerkennen:
wir werden uͤberdieß bald neue Beweise fuͤr die Genauigkeit unserer
Formeln sehen.
25) Wenn man die Zahlen pruͤft, welche in der lezten Columne zur Rechten der
Tabelle eingetragen sind, so wird man bemerken, daß das Maximum der
Quantitaͤt der Wirkung des Rades fuͤr den Versuch 27 eintrat, indem er
0,6667 oder 2/3 der Umdrehung dieses Rades gewaͤhrte. Um diese
Geschwindigkeit mit jener zu vergleichen, welche im naͤmlichen Falle durch
die Theorie angegeben wird, so muͤßte man die mittlere Geschwindigkeit des
Wassers in dem Augenblike kennen, wo es in die Krummen tritt: nun gibt es nur
unmittelbare Erfahrungen uͤber die Beschaffenheit derselben, welche am Ende
dieser Abhandlung werden beschrieben werden, und welche uns dieselbe auf eine
hinreichend genaue Weise geben koͤnnten; das Mittel, welches anfangs von
Smeaton fuͤr den Fall von Raͤdern mit gewoͤhnlichen Schaufeln
angewendet wurde, wuͤrde hier in der That zu wenig genuͤgenden
Resultaten fuͤhren, in Betracht der eigenthuͤmlichen Form der
Schaufeln.
Um, von einer anderen Seite, den mittleren und absoluten Werth der Geschwindigkeit
unseres Rades kennen zu lernen, welcher der Zahl der obigen Umdrehungen entspricht,
muͤßte man anfangs wissen, in welcher Entfernung vom Mittelpuncte dieses
Rades man den Mittelpunct des mittleren Drukes des Wassers annehmen muͤßte;
alles dieß macht folglich die Werthbestimmung des genauen Verhaͤltnisses des
Rades und Wassers fuͤr den Augenblik des Maximum der Wirkung schwierig.
Man kann aber hier auf eine andere Weise den oben angestellten Constructionen (Fig. 7.) zu Huͤlfe
kommen; es ist wirklich offenbar, daß, wenn man bis zu ihrem Durchschneiden in D, mit der Achse, AT,
der Abscissen, die gerade Linie, MC,
verlaͤngert, welche das Gesez der durch den Versuch gegebenen Versuche
darstellt, die Entfernung, AD, dieses Punctes vom
Ursprunge, nach dem Maßstabe, fuͤr jene genommen werden kann, welche die Zahl
der Umdrehungen ausdruͤkt, die einem Druke = o,
der vom Wasser auf das Rad ausgeuͤbt wird, und folglich der mittleren
Geschwindigkeit des Wassers selbst entspricht. Man findet daher diese Zahl = 1,282,
deren umgekehrtes Verhaͤltniß zu 0,6667, die dem Maximum der Wirkung
entspricht, 0,52 ist; dieß entfernt sich sehr wenig von dem durch die Theorie (4)
gegebenen Verhaͤltnisse; die geringe Differenz, welche Statt hat, kann der
Ungewißheit zugeschrieben werden, die natuͤrlicher Weise bei der wahren
Stellung des Maximums Statt findet, weil die Quantitaͤten der Wirkung gegen
diese Stellung, nur in fast unmerklichen Stufen variiren, wie es die Tabelle der
Versuche selbst anzeigt.
26. Es bleibt uns uͤbrig, die Quantitaͤt der vom Rade gelieferten
Wirkung fuͤr den Fall des Maximum der Wirkung zu bestimmen; eine
Quantitaͤt, welche, nach den Tabellen, 0k,5282 gehoben auf 1m,00
fuͤr die Secunde, jener gleich ist, welche wirklich durch das bewegende
Wasser aufgewendet wurde.
Da die gelieferte Quantitaͤt Wassers in einer Secunde, nach dem Versuche (21),
3 Liter, 8942 ist, was im Gewichte 3k,8942
betraͤgt: so handelt es sich darum, diese Quantitaͤt durch die
Hoͤhe zu multipliciren, welche der mittleren und effectiven Wirkung zukommt,
die das Wasser im Augenblike seines Eintrittes in die Eimer des Rades besizt, um
Ergebnisse zu erhalten, welche sich mit jenen der Theorie und mit jenen, die von
verschiedenen Schriftstellern, namentlich von Smeaton geliefert wurden, genau
vergleichen lassen: wir finden also hier die naͤmliche Schwierigkeit, auf
welche wir oben stießen, ohne die naͤmlichen Mittel zu ihrer Hebung zu
haben.
Nenn man sich mit Annaͤherung begnuͤgen will, so wird man immer die
Geschwindigkeit, um die es sich handelt, nach der Zahl der Umdrehungen
schaͤzen koͤnnen, welche dem unbelasteten Rade entspricht, das nichts
desto weniger der Wirkung des Stromes ausgesezt wurde; die Construction gab uns (25)
fuͤr diese Zahl 1t,2775, die man
noch mit dem Umkreise des Rades, der dem mittleren Faden des Wassers im Laufe
entspricht, multipliciren muß; nimmt man nun diesen Faden als in der Mitte des Durchschnittes befindlich an,
so wird noch die Hoͤhe dieses lezteren zu bestimmen uͤbrig bleiben,
was nicht leicht ist, da sie selbst von der Geschwindigkeit abhaͤngt, welche
man finden soll. Wenn man nun erwaͤgt, daß die Hoͤhe des
Durchschnittes des Wassers am Rade nicht viel von jener, die = 0m,03, verschieden seyn kann, welche der
Oeffnung des Schuzbrettes angehoͤrt, so daß die Differenz, wenn eine Statt
findet, nur ein sehr kleiner Bruch des mittleren Halbmessers, den man sucht, seyn
kann; so werden wir hinreichend ermaͤchtigt seyn, fuͤr diesen
Halbmesser die Entfernung des Mittelpunctes des Rades von jenem Puncte anzunehmen,
welcher sich bei 0m,015 uͤber dem
Grunde des Laufes unter der Achse dieses Rades findet. Da die Entfernung bis zum
Grunde des Laufes, nach geraden Messungen, 0m,251 ist; so wird der mittlere Halbmesser des Rades 9m,236 seyn, und sein mittlerer Umkreis 1m,483 ; folglich wird die gesuchte
Geschwindigkeit 1m,483 × 1t,2775 = 1m,895 zu ihrem Werthe haben, welchem die
Hoͤhe des Falles 0m,183 entspricht.
Wenn man nun diese Hoͤhe mit dem Aufwande 3k,8942 multiplicirt, der durch den Versuch
gegeben wurde; so wird fuͤr die Quantitaͤt der vom Wasser des
Behaͤlters gelieferten Wirkung, 0k,7126 erhoben zu 1m,00 fuͤr
die Secunde kommen; da dieses vom Rade gelieferte Maximum, 0k,5282 ist, so wird sein Verhaͤltniß
zum Ersten Bruche 0,741 gleich seyn.
Dieses Verhaͤltniß ist fast 2 1/2 Mahl dasjenige, welches Smeaton fuͤr
die Raͤder mit gewoͤhnlichen Schaufeln gefunden hat, und entfernt sich
nicht von dem Ergebnisse bei den besten bekannten hydraulischen Raͤdern. Die
Theorie, welche im ersten Theile dieser Abhandlung aufgestellt wurde, findet sich
also auch durch die absoluten Quantitaͤten der Wirkung, so viel es nur immer
durch die Erfahrung moͤglich wird, gerechtfertigt; denn man wird sich
erinnern, daß diese Theorie auf mehrere Umstaͤnde, welche in der Praxis Statt
finden, nicht Ruͤksicht nimmt, wie z.B. auf den Verlud durch das Spiel im
Laufe, den Stoß des Wassers gegen das Rad, die Geschwindigkeit, welche es nach dem
Austritte behaͤlt, und endlich den Widerstand, den es durch sein
Hinaufsteigen nach der Laͤnge der Krummen erleidet. –
27. Wenn es erlaubt waͤre, die mittlere Geschwindigkeit 1m,895, die man oben erhielt, als ganz genau zu
betrachten, so wuͤrde man, in Vergleichung derselben mit der Geschwindigkeit
2m,073, weiche nach der Theorie der
Hoͤhe des Wassers 0m,219
uͤber dem Mittelpuncte des Schuzbrettes zukommt, finden, daß sie nur
ungefaͤhr 0,92 ist; so daß die 8 Hundertel der Geschwindigkeit des Wassers
beim Austritte aus diesem Schuzbrette, durch die Wirkung der Widerstaͤnde und
der Zusammenziehungen, welche es außen und innen im Behaͤlter erleidet,
verloren gehen. Wir werden spaͤter, durch unmittelbare Versuche, sehen, daß
diese Zahlen sich sehr wenig von den wahren entfernen, und daß die Differenz 0,08
vorzuͤglich dem Umstande zuzuschreiben ist, daß das Wasser aus der Schleuse
mit einer geringeren Geschwindigkeit ausstießt, als die Theorie anzeigt. Wenn man
uͤberdieß die Faͤlle vergleicht, welche den Geschwindigkeiten 1m,895 und 2m,073 entsprechen, so wird man finden, daß
sie unter sich im Verhaͤltnisse von (1,895)² zu (2,073)²
stehen, welches gleich ist (0,92)², oder 0,846; so daß der Fall des Wassers
am Schuzbrette, um ungefaͤhr 15 Hundertel durch obige Ursachen
geschwaͤcht wird. Um auf gleiche Weise den effectiven Aufwand, der
ungefaͤhr 3k,8942 betraͤgt,
mit dem theoretischen zu vergleichen, wird man bemerken, daß die Oeffnung des
Schuzbrettes dort 3 Cent., und seine Breite ungefaͤhr 76 Mill.
betraͤgt; was fuͤr die Breite, durch welche das Wasser entflieht, 0m,00228 macht; da ferner die
Geschwindigkeit, welche der Hoͤhe uͤber dem Mittelpuncte der Oeffnung
zukommt, nach dem Vorhergehenden 2m,0727
fuͤr die Secunde ist; so wird der theoretische Aufwand waͤhrend
derselben Zeit 0,00228. 2,0727 = 0m,0047258, oder 4k,7258 dem Gewichte
nach betragen: eine Quantitaͤt, deren umgekehrtes Verhaͤltniß zu
jenem, das unmittelbar durch den Versuch gegeben wurde, 0,824 ist.
28) Man wird vielleicht neugierig seyn zu wissen, ob das Verhaͤltniß 0,741 der
gefundenen Quantitaͤten der Wirkung in n°.
26. genau der Coefficient ist, welcher der theoretischen Formel der Druke P, zukommen muß. Um dahin zu kommen, gibt es kein
anderes Mittel, als diese Formel mit jener zu vergleichen, die durch die Gleichung
der geraden Linie, MC (Fig. 7.) der durch das Rad
gehobenen Gewichte gegeben wuͤrde: nun haben wir schon gefunden, daß die
Abscisse des Punctes, D, der einem Gewichte = 0
entspricht, 1,2775 des Rades darstellte, und auf der anderen Seite gibt die
Construction fuͤr das Gewicht, AD, das
einer Geschwindigkeit = 0 des Rades entspricht, 7k,55 : daher hat man, indem man auf die respectiven Maßstaͤbe der
Ordinaten und der
Abscissen (22) Ruͤksicht nimmt, und durch t,
uͤbrigens die Zahl der Umdrehungen ausbruͤten laͤßt, welche
irgend einem durch das Rad gehobenen Gewichte, p,
entspricht,
p = 75500/12775 (1,2775 – t)
Aber nach (21) und (26) erhebt sich das Gewicht, p, zu
einer Hoͤhe 0,2188, wahrend der Mittelpunct des mittleren Drukes des Rades
den Umkreis 1m,483 beschreibt: folglich
besteht zwischen p und dem Druke P, der auf diesen Umkreis ausgeuͤbt wird, das Verhaͤltniß
p. 0,2188 = P. 1,483.
Da, auf der anderen Seite, v, im Allgemeinen die
Geschwindigkeit des Mittelpunctes des Drukes, worum es sich handelt, ist, so hat
man, v = 1m,483t ; wenn man nun daraus die Werthe von
t und p, zieht, und sie
in obiger Gleichung substituirt; so wird nach Anstellung der ganzen Berechnung,
P = 0,58797 (1,895 – v) Kil.
Dieß ist die Gleichung, welche man nun mit folgender
vergleichen muß:
P = 2m (V – v) Kil. = 203,8943 D (V – v) Kil.,
welche Art. 4. gefunden wurde, und worin D, das Volumen des Wassers, das in einer Secunde
ausfließt, bezeichnet; aber man hat hier, (21) und (26),
D = 0m,0038942
und V = 1m,895;
daher wird diese Gleichung werden:
P = 0,794022 (1,895 – v) Kil.
Man steht, daß sie sich von der ersten absolut nur durch den Werth der Coefficienten
unterscheidet, und daß das Verhaͤltniß 0,58797/0,794022 = 0,740 dieser
Coefficienten sich nur um ein Tausendtheil von jenem 0,741 entfernt, welches oben
fuͤr die Quantitaͤten der Wirkung des Wassers und des Rades in Bezug
auf das Maximum der Wirkung gefunden wurde; dieß ist ein Grad von
Annaͤherung, den man bei Versuchen der Art, wie die unsrigen, nicht erwarten
sollte.
29) Wir glaubten auf dem vorausgehenden Beispiele fest bestehen, und es unter allen
Gesichtspuncten – pruͤfen zu muͤssen, da die Versuche, welche
sich darauf beziehen, und die in der Tabelle von n°. 21. dargestellt sind, mit viel Sorgfalt angestellt wurden, und
weil sie auf eine gewisser Massen strenge Art die Anwendungen des Principes der
lebendigen Kraͤfte bei hydraulischen Raͤdern zu beweisen dienen, nicht nur, wie man sich
gegenwaͤrtig begnuͤgte, es fuͤr alle einzelnen Umstaͤnde
der Wirkung dieser Raͤder zu thun, sondern fuͤr die ganze Reihe der
Wirkungen, welche sie unter Wirkung einer gleichen bewegenden Kraft hervorbringen
koͤnnen; denn die Ergebnisse, welche vorausgehen, beweisen, daß die
naͤmlichen Coefficienten fuͤr alle Werthe der von diesem Principe
hergeleiteten Formeln anwendbar sind.
Unsere Beweise beschraͤnkten sich uͤberdieß nicht auf dieses einzige
Beispiel, und wir koͤnnten viele andere anfuͤhren, wenn wir nicht
befuͤrchteten, diese Abhandlung zu sehr in die Laͤnge zu ziehen, und
uns von unserem speciellen Gegenstande zu entfernen.
30. Man wird sich erinnern, daß es sich darum handelt, die Quantitaͤten der
Wirkung, die von dem neuen Rade und von dem Wasser, das darauf wirkt, geliefert
werden, unter sich, in den verschiedenen Faͤllen, zu vergleichen, um auf eine
genaue Weise die Vortheile, die diesem Rade eigen seyn duͤrften, und die
besonderen Umstaͤnde, wo diese Vortheile fuͤr ihre Anwendung in der
Praxis Statt finden werden, wuͤrdigen zu koͤnnen. Nun sind wir noch
nicht im Stande, diese Fragen auf eine genuͤgende Weise zu loͤsen,
indem wir noch nicht mit Genauigkeit die mittlere Geschwindigkeit des Wassers am
Rade kennen, und man doch diese Geschwindigkeit kennen muß (26), wenn man Ergebnisse
erhalten will, die sich mit jenen der Theorie vergleichen lassen.
Das oben angewandte Mittel (26), außerdem, daß es langweilig und muͤhsam ist,
ist uͤberdieß zu unbestimmt, als daß man die Werthe, zu welchen es
fuͤhrt, als der Wahrheit hinlaͤnglich nahe kommend betrachten
koͤnnte; daher ist das Erste, womit wir uns jezt zu beschaͤftigen
haben, dieses, die Umstaͤnde des Fließens des Wassers durch Schuzbrett und
Lauf, die wir gebrauchten, durch eine Reihe von Versuchen zu bestimmen; wir werden
diese Versuche zum Gegenstande des lezteren Theiles dieser Abhandlung machen, und,
um diese fuͤr jezt auf das moͤglich Beste zu vervollstaͤndigen,
schließen wir damit, die Tabelle der verschiedenen Ergebnisse der Versuche und
Berechnungen uͤber das Rad fuͤr das Maximum der Wirkung zu geben,
indem die Oeffnungen des Schuzbrettes und die Hoͤhe des Wassers im
Behaͤlter abwechselten, und zwar in hinlaͤnglich ausgedehnten
Graͤnzen in Bezug auf die Dimensionen, welche fuͤr dieses Rad
angewendet wurden.
Tabelle uͤber die Resultate der Versuche, welche
mit dem Rade unter verschiedenen Lasten des Wassers und Oeffnungen des Schuzbrettes
angestellt wurden.
Textabbildung Bd. 19, S. 455
Nummern der Versuche; Hoͤhe
der Oeffnung des Schuzbrettes; Hoͤhe des Wassers uͤber dem
Aussprunge des Schuzbrettes; Effectiver Aufwand an Wasser in I. Secunde
ausgedruͤkt in Gewicht; Verhaͤltniß des wirklichen Aufwandes zum
Theoretischen; Zahl der Umdrehungen des Rades, fuͤr das Maximum der
Wirkung; Geschwindigkeit des aͤußeren Umkreises des Rades beim Maximum;
Quantitaͤt des Maximum der Wirkung des Rades
Bemerkungen.
31. Nach dem, was vorlaͤufig gesagt wurde, scheint es nicht nothwendig,
uͤber die Bildung dieser Tabelle in das Einzelne zu gehen; ich werde mich
begnuͤgen, einige Betrachtungen uͤber die Unregelmaͤßigkeiten
zu geben, welche sich in der 5ten Columne zwischen den Verhaͤltnissen des
wirklichen und theoretischen Aufwandes finden.
Diese Unregelmaͤßigkeiten werden, wie man steht, besonders fuͤr die
Oeffnungen des Schuzbrettes von 3c. Statt haben, die dem
großen Aufwande an Wasser entsprechen: hieruͤber wird man nicht sehr staunen,
wenn man bedenkt, daß dann eine groͤßere Ungewißheit in der Beobachtung des
Aufwandes herrschen muß. Man wuͤrde sich jedoch betruͤgen, wenn man
sie dieser einzigen Ursache zuschriebe; denn die Zahlen der 5ten Columne
haͤngen nicht nur von dem wirklichen Aufwande an Wasser, sondern auch vom
bestimmten Maße der Breite der Muͤndung ab, welches in unserem Falle nicht
leicht zu bestimmen ist, und woruͤber man sich nur um ein Dreißigstel
tauschen duͤrfte, um Differenzen von mehreren Hunderteln in den
Verhaͤltnissen des wirklichen Aufwandes zum theoretischen zu bekommen. Diese
Verhaͤltnisse, wie sie in der 5ten Columne eingetragen sind, muͤssen
daher nicht als absolute Zahlen betrachtet werden, um so mehr, als die
bezuͤglichen Versuche in Zwischenraͤumen von oͤfters mehreren
Tagen angestellt wurden; so daß außer der Unmoͤglichkeit die Hoͤhen
des Schuzbrettes auf eine bestaͤndige Art zu bestimmen, auch einige Unordnung
im Systeme der Zimmerung sich einstellen koͤnnte. Da nun die Umstaͤnde
des Fließens nicht die naͤmlichen waren, ist es unmoͤglich, daß die
Ergebnisse vollkommen unter sich uͤbereinstimmen. Alles, was wir fuͤr
den Augenblik erkannt und angenommen wissen wollen, ist, daß diese Ergebnisse alle
vorzuͤglich in so fern sehr genau sind, als sie die bestimmte Beobachtung der
Hoͤhe des Wassers und stilles Aufwandes betreffen: die einzigen Daten, die
uns zur Werthbestimmung der Quantitaͤt der vom Wasser gelieferten Wirkung
unerlaͤßlich sind, und die immer mehrmahls mit aller wuͤnschenswerthen
Genauigkeit in den Versuchen dieser Art bestimmt wurden.
32. Um in diesem Bezuge gar keinen Zweifel uͤbrig zu lassen, wird es an einer
einzigen Bemerkung genuͤgen; die Versuche N°. 6 und 11. sind jene, deren in die 5te Columne eingetragene Zahlen die
groͤßte Anomalie in Bezug auf die benachbarten Versuche darbieten, weil sie
um einige Hundertel schwaͤcher sind; nun wurden von diesen Versuchen immer
zwei am naͤmlichen Tage und in einem von den uͤbrigen entfernten
Zeitraume angestellt; und, was die Unordnung betrifft, welche in der Zimmerung des
Schuzbrettes Statt finden konnte, haben wir den Beweis hieruͤber erlangt, als
wir am Ziele einer bestimmten Zeit die Messung der Breite der Schleuse und des
Laufes wieder vornehmen wollten: diese Breite, welche anfaͤnglich 8e. war, wurde zu 0m,076 befunden, und selbst 0m,074; so daß durch die Wirkung der Feuchtigkeit, oder anderer Ursachen, sie
um mehr als ein Zwanzigstel geaͤndert wurde.
In der Werthbestimmung der Zahlen der 5ten Columne suchte man, so viel als
moͤglich, diese Ursache des Irrthurmes in Rechnung zu bringen; indessen, da
sie nur am Ziele einer gewissen Zeit beobachtet wurde, konnte man nicht annehmen,
daß diese Zahlen mit Genauigkeit die Verhaͤltnisse des wirklichen Aufwandes
zum Theoretischen anzeigten. Wir werden spaͤter auf diesen Gegenstand
zuruͤkkommen, indem wir die ganze Reihe von Versuchen uͤber das
Fließen wiederholen, so daß wir vollkommen vergleichbare Ergebnisse erhalten.
Fuͤr den Augenblik genuͤgt es, bewiesen zu haben, daß die Anomalien
der Zahlen der fuͤnften Columne der obigen Tabelle nicht ganz den Fehlern der
Beobachtung des wirklichen Aufwandes zukommen, welche, wie ich wiederhole, immer mit
der groͤßten Sorgfalt und mehrmahls gemacht wurde.
Dritter Theil. Versuche uͤber die Geseze des
Ausfließens des Wassers in dem angewendeten Apparate.
33. Ehe wir die Ergebnisse dieser Versuche darlegen, ist es gut, im Voraus zu
erinnern, daß sie weder in der naͤmlichen Zeit, noch in dem naͤmlichen
Locale mit den vorhergehenden angestellt wurden; Umstaͤnde, welche nicht von
meinem Willen abhingen und welche ich schon am Anfange des zweiten Theiles
auffuͤhrte, zwangen mich den Apparat auf einen anderen Lauf des Wassers zu
verlegen; man muß daher nach dem, was uͤber die vorhergehenden Versuche
bemerkt wurde, erwarten, einige Unterschiede zwischen den neuen und alten
Ergebnissen in Bezug auf den Verbrauch zu finden. Allein da man die groͤßte
Sorgfalt anwendete, um die Dinge in ihren alten Stand zu versezen, und uͤberdieß die Einrichtung
des Behaͤlters, des Schuzbrettes und des inneren oder aͤußeren Laufes
nicht geaͤndert wurde, so ist man noch immer berechtigt, einen großen Theil
dieser Unterschiede auf Rechnung der Fehler zu sezen, welche bei Schaͤzung
der Oeffnung der Schleuse begangen wurden, und folglich die Umstaͤnde und
Geseze des Ausfließens des Wassers in jeder Hinsicht als genau aͤhnlich zu
betrachten, d.h. mit anderen Worten, daß wir fuͤr alle Faͤlle die
Geschwindigkeiten des Wassers, welche dem naͤmlichen Falle und der
naͤmlichen Hoͤhe des Schuzbrettes zukommen, als dieselben annehmen
koͤnnen. Wenn man ferner in der Folge dahin kommen wird, aus diesen Versuchen
das Maß der Quantitaͤten der Wirkung des Wassers abzuleiten, wird man Sorge
tragen, die verschiedenen Ursachen zu eroͤrtern, welche die Schlußfolgen
schwaͤchen oder bestaͤtigen koͤnnen, welche man daraus folgern
will, und welche den Gegenstand dieser Abhandlung ausmachen.
34. Wir haben bereits gezeigt, wie es uns gelang, im Allgemeinen mit
genuͤgender Approximation, den Verbrauch an Wasser in einer Secunde, unter
verschiedenem Falle und bei verschiedenen Oeffnungen des Schuzbrettes zu bestimmen;
es bleibt uns noch uͤbrig zu erklaͤren, wie wir hier verfuhren, um die
Geschwindigkeit am Rade zu erhalten.
Das gewoͤhnlich gebraͤuchliche Mittel besteht, wie man weiß, darin,
sich eines sehr leichten Drehkreuzes zu bedienen, das auf dem Strome angebracht ist;
da aber dieses Mittel in dem gegenwaͤrtigen Falle nicht ohne Unbequemlichkeit
ist, und uͤberdieß einige Ungewißheit uͤber das Maß der mittleren
Geschwindigkeit laͤßt, so bedienten wir uns der Methode der Durchschnitte,
die ohne Widerrede den Vorzug verdient, da man den Ausfluß des Stromes kennt. Da wir
uͤbrigens den Durchschnitt des Wassers mit aller moͤglichen
Genauigkeit erhalten wollten, ließen wir uns eine Art von Kaͤmmen machen, von
der in Fig. 8.
angedeuteten Form. Diese Kaͤmme bestehen aus einem prismatischen
Stuͤke Holz, AB, welches eine
hinlaͤngliche Laͤnge besizt, um sich an den Enden auf dem oberen
Theile der senkrechten Seitenwaͤnde, ab,
und, cd, des Laufes oder Kanales stuͤzen zu
koͤnnen. Dieses Stuͤk ist an zweien seiner Seiten mit verschiedenen in
einer Entfernung von 4 bis 5 Mill. stehenden Loͤchern senkrecht durchbohrt,
welche Loͤcher gerade Stifte aus Eisendraht aufnehmen, deren untere
zugespizte Enden bestimmt sind, so genau als moͤglich in Beruͤhrung mit der Oberflaͤche
des Wasses zu kommen, ohne jedoch in dasselbe einzudringen, was; man, wann der Strom
keine merkliche Fluctuationen erleidet, leicht durch Uebung erlernt.
35. Es ist einleuchtend, daß man durch dieses Verfahren sowohl den Durchschnitt der
oberen Flaͤche des Wassers, als auch jenen des Grundes, des Laufes sehr genau
erhalten, und leicht auf ein Brett oder einen Schiefer uͤbertragen kann,
indem man gegen einen seiner Vorspruͤnge, welcher vorlaͤufig gut
gerichtet ist, die untere Flaͤche des Querstuͤkes, AB, des Instrumentes anbringt. Wenn man
uͤbrigens annimmt, daß man in Voraus auf dem Brette die senkrechten Linien,
ab, und, cd,
gezogen hat, welche die Seitenwaͤnde des Laufes vorstellen, so daß man den
oberen Durchschnitt des Wassers, efg, und jenen,
bc, des Grundes des Laufes genau auf einander
passen kann, so wird man nur mehr den Flaͤcheninhalt zwischen diesen
Durchschnitten und den geraden Linien, ab, und,
cd, mittelst gleich entfernter
Parallel-Linien, zu berechnen haben, was, wie man weiß, nur eine Addition und
Multiplication kostet.
36. Der Quotient des Ausflusses des Stromes durch den also gefundenen
Flaͤcheninhalt gibt die mittlere Geschwindigkeit des Wassers auf eine
absolute und hinlaͤnglich angenaͤherte Weise; denn man kann sich
hoͤchstens um ein Viertel Millimeter uͤber die Hoͤhe einer
jeden Ordinate des Durchschnittes taͤuschen, wenn man Gelaͤufigkeit in
solchen Operationen erlangt hat, und der mittlere Fehler muß noch geringer seyn.
Wenn also die Dike der in den Lauf getretenen Wasser-Schichte ungefaͤhr 1
oder 2 oder 3 Centimeter waͤre, so wuͤrde die Totalitaͤt des
bei der Messung des Flaͤcheninhaltes des Durchschnittes begangenen Fehlers
geringer seyn, als das 40stel, 80stel oder 120stel dieses Flaͤcheninhaltes,
und man wird bemerken, daß dieser Fehler sich nochwendig verringert, und folglich
dienen wird, die Schaͤzung der mittleren Geschwindigkeiten des Wassers am
Durchschnitte zu vergroͤßern; denn da die Enden der Stangen nothwendig in
Beruͤhrung mit dem Wasser stehen, so sind die Ordinaten des Durchschnittes
eher schwaͤcher als staͤrker.
Ueberdieß ist es noͤthig die Durchschnitte nur in dem Augenblike zu nehmen, wo
das Ausfließen des Wassers ganz gleichfoͤrmig geworden ist, und eine, so zu
sagen, unbewegliche Flaͤche darbietet ohne Streifen und ohne Fluctuation:
dieß erhaͤlt man immer, wann die Hoͤhe des Wassers im Behaͤlter gut geregelt und kein
Hinderniß da ist, welches sich seiner Bewegung beim Austritte aus der Schleuse oder
im Laufe entgegenstellt. Man wird uͤberdieß einen großen Theil der Versuche
vermeiden, welche noͤthig sind, um die Spizen der Stangen in
Beruͤhrung mit der Oberflaͤche des Wassers zu bringen, wenn man, statt
diese Stifte bloß durch das Stuͤk, AB,
laufen, und dort mittelst der Reibung allein festhalten zu lassen, man ihr Einsenken
durch einen Theil von Schraubengaͤngen, der an jedem derselben angebracht
ist, regelt, in dem Theile naͤmlich, der diesem Stuͤke entspricht.
37. Um nichts Wesentliches zu vernachlaͤssigen, muͤssen wir Ans
zuruͤkrufen, daß die Seitenwaͤnde des Laufes, welcher zu unsern
Versuchen diente, kreisfoͤrmige Vertiefungen; REC, (Fig.
2. und 3.) tragen, welche bestimmt sind, die Ringe des Rades aufzunehmen, welche
also die Verlaͤngerungen des vorderen Theiles dieser Seitenwaͤnde
bilden. Bevor wir daher einen Versuch uͤber das Ausstießen begannen, hielten
wir es fuͤr zwekmaͤßig, diese Vertiefungen mit kleinen Brettern
einzufassen, welche genau an die Waͤnde des Laufes anschließen, und dieses
zwar um die Sachen sast in den naͤmlichen Stand zu sezen, als ob man mit dem
Rade arbeitete, und uͤberdieß eine zu große Unfoͤrmlichkeit im
Durchschnitte der Wasserschichte zu vermeiden. Nachdem hierauf die Oeffnung des
Schuzbrettes und die Hoͤhe des Wassers im Behaͤlter gehoͤrig
geregelt waren, konnten wir mit einiger Genauigkeit den Durchschnitt unter der Achse
des Rades in CC
' (Fig. 2. und 3.) d.h.
ungefaͤhr in 11 Cent. des Schuzbrettes, nehmen, und daraus die
Geschwindigkeit des Wassers am naͤmlichen Orte ableiten: ein
aͤhnliches Verfahren, neben dem zusammengezogenen Durchschnitte wiederholt,
d.i. in einer Entfernung von dem oberen Vorsprunge der Schleuse, welche fast ihrer
halben Hoͤhe gleichkommt, erlaubte uns die groͤßte Geschwindigkeit des
Wassers beim Austritte aus der Schleuse herzuleiten; das Verhaͤltniß zwischen
diesen beiden Geschwindigkeiten war uͤberdieß unmittelbar durch das
umgekehrte Verhaͤltniß der entsprechenden Durchschnitte angegeben.
Obgleich die Berechnung dieses Verhaͤltnisses und der Geschwindigkeit beim
Austritte aus dem Schuzbrette fuͤr unseren Zwek eben nicht
unerlaͤßlich war, glaubten wir doch die Ergebnisse in der folgenden Tabelle
anzeigen zu muͤssen, da sie nuͤzliche Bemerkungen veranlassen
koͤnnen. Aus dem naͤmlichen Grunde verglichen wir auch die
Geschwindigkeit des Wassers am Schuzbrette mit der mittleren Geschwindigkeit, die
durch die bekannten Formeln ausgedruͤkt ist, und welche beinahe, wie man
weiß, von der Hoͤhe des Niveaus uͤber dem Mittelpuncte der Oeffnung
abhaͤngt. Um endlich gar nichts zu vernachlaͤssigen, was einiges
Interesse haben koͤnnte, berechneten wir den theoretischen Ausfluß oder
Verbrauch des Wassers und sein Verhaͤltniß zum wirklichen Verbrauche, der
sich aus den Versuchen ergab.
Tabelle, welche die Ergebnisse der Versuche enthaͤlt,
welche uͤber das Ausfließen des Wassers, unter verschiedenem Falle und bei
einer Oeffnung des Schuzbrettes von 1 Cent. angestellt wurden.Man wird ohne Muͤhe bemerken, daß die Zahlen der siebenten Columne der
Tabelle die Product Zahl 1,2346 sind, welche (42) das Verhaͤltniß
100/1 des Flaͤchenraumes des zusammengezogen Durchschnittes
darstellt; eben so sind auch die Zahlen der neunten Columne die Producte der
entsprechenden Zahlen der siebenten und achten Columne.
Nummern der Versuche.
Hoͤhe des Wassers uͤber dem Grunde des
Schuz-Brettes.
Wirklicher Verbrauch an Wasser in Litres.
Verbrauch nach der Theorie.
Verhaͤltniß des wirklichen und theoretischen
Verbrauches, od. d. Geschwindigkeiten am Schuz-Brette.
Geschwindigkeit des Wassers am Schuz-Brette nach d.
Theorie.
Verhaͤltniß der wirkl. Geschwindigkeiten beim
zusammengezogenen Durchschnitte zu den theoretischen.
Verhaͤltnisse der wirklichen Geschwindigkeiten
unter dem Rade, und bei zusammengezogenem Durchschnitte
Verhaͤltnisse der Geschwindigkeiten unter dem
Rade zu den theoretischen Geschwindigkeiten
M.
lit.
lit.
M.
1
0,277
1,426
1,756
0,812
2,310
1,002
0,853
0,855
2
0,249
1,343
1,663
0,808
2,188
0,997
0,855
0,852
3
0,227
1,269
1,586
0,800
2,087
0,988
4
0,197
1,191
1,475
0,807
1,941
0,996
5
0,182
1,144
1,416
0,808
1,863
0,988
6
0,170
1,105
1,367
0,808
1,799
0,998
0,858
0,856
7
0,147
1,014
1,268
0,800
1,669
0,987
8
0,132
0,949
1,199
0,792
1,578
0,997
9
0,119
0,900
1,131
0,796
1,488
0,982
0,871
0,855
10
0,102
0,825
1,039
0,794
1,367
0,980
11
0,090
0,773
0,981
0,788
1,291
0,972
12
0,082
0,727
0,934
0,779
1,229
0,961
0,885
0,851
Bemerkungen.
38. Die Betrachtung der fuͤnften Columne dieser Tabelle scheint anzuzeigen,
daß das Verhaͤltniß des wirklichen Verbrauches oder Ausflusses zum
theoretischen Verbrauche, oder, was dasselbe ist, das Verhaͤltniß der
wirklichen Geschwindigkeit zur theoretischen Geschwindigkeit an dem Schuzbrette sich
mit der Hoͤhe des Wassers im Behaͤlter vermindert, und da das Profil
nahe am zusammengezogenen Durchschnitte im ganzen Laufe der Versuche nicht auf eine
merkliche Weise abgeaͤndert wurde, so muß man daraus noch schließen, daß die
wirklichen Geschwindigkeiten des Wassers am zusammengezogenen Durchschnitte sich um
so viel mehr von den theoretischen Geschwindigkeiten unterschieden, je geringer der
Fall war; dieses ist klar genug in der siebenten Columne angezeigt, welche die
Verhaͤltnisse dieser Geschwindigkeit enthaͤlt.
Man steht uͤberdieß, daß die Verminderung der Geschwindigkeit nur bei sehr
kleinen Faͤllen gehoͤrig bestimmt werden kann, was ohne Zweifel davon
abhaͤngt, daß der Durchschnitt des Wassers beim Eingange des inneren Canales,
fgh, g'h'
(Fig. 1.
und 2.), wovon
Art. 17. die Rede war, dann dem Flaͤchenraume der Schleuse sehr nahe kommt.
Man wird in der That bemerken, daß das Verhaͤltniß der Geschwindigkeiten und
das Verhaͤltniß des wirklichen Verbrauches zum theoretischen Verbrauche auf
eine merkliche Weise nur beim Abflusse von der Hoͤhe des Falles 17. an
abnehmen: nun ist diese Hoͤhe nicht sehr verschieden von jener, fg, welche die Bretter hatten, die den inneren
Canal bildeten. Die naͤmliche Bemerkung findet ihre Anwendung auch auf die
Ergebnisse der Versuche, welche uͤber die Oeffnungen des Schuzbrettes von 2
und 3 Cent. gemacht wurden, und die spaͤter dargelegt werden sollen.
39. Nach den Zahlen der achten Columne kann man auch schließen, daß das Wasser einen
großen Verlust an Geschwindigkeit von Seite des aͤußeren Laufes erleidet, und
daß das Gefaͤll von Einem Zehntel, welches man ihm gegeben hat, nach Anzeige
verschiedener Schriftsteller, bei weitem nicht hinreicht, diesen Verlust im
gegenwaͤrtigen Falle, bei einer Wasserschichte von 1c, zu ersezen; immer scheint, wie man bereits gesehen hat, der Widerstand
mit der Geschwindigkeit abzunehmen.
40. Wir haben so eben gesagt, daß der Durchschnitt des zusammengezogenen Fadens
waͤhrend der Dauer aller Versuche sich nicht merklich aͤnderte; wir haben uns davon
auf eine bestimmte Art uͤberzeugt, indem wir eines der oben beschriebenen
Instrumente (34) an diesem Durchschnitte anbrachten und dort ließen, waͤhrend
wir die Hoͤhe des Wassers im Behaͤlter innerhalb der Graͤnzen
der verschiedenen Versuche abaͤndern ließen; nachdem die Spizen der Stifte so
genau als moͤglich in Beruͤhrung mit der oberen Flaͤche des
Wassers gebracht worden waren, dessen Durchschnitt eine wahre gerade horizontale
Linie war, bemerkte man bestaͤndig, sowohl fuͤr die Oeffnung des
gegenwaͤrtigen Schuzbrettes, als auch fuͤr die verschiedenen anderen
Oeffnungen, die zum Versuche benuͤzt wurden, daß die Spizen keinen Augenblik
aufhoͤrten, die obere Oberflaͤche des Wassers zu beruͤhren; nur
fand die Beruͤhrung nicht Statt, wann die Hoͤhe des Wassers im
Behaͤlter so schwach wurde, daß das Ausfließen auf eine regelmaͤßige
Weise fuͤr jene Hoͤhen aufhoͤrte, welche sich außer den
Graͤnzen unserer Versuche befanden.
41. Uebrigens schien das Wasser genau den Waͤnden des Laufes neben dem
Schuzbrette zu folgen, und die Zusammenziehung verrieth sich nur durch eine leichte
Senkung der oberen Flaͤche, deren Durchschnitt, wie wir sagten, eine
vollkommen gerade Linie war; die groͤßte Senkung hatte Statt bei einer
Entfernung von ungefaͤhr 5 bis 6 Mill. des oberen Vorsprunges der Schleuse,
d.h. einer Entfernung, die ungefaͤhr ihrer halben Oeffnung gleich ist;
uͤber diese Stelle hinaus zeigte der Durchschnitt des Wassers an den Seiten
eine leichte Eindruͤkung, welche in, e'f'g', (Fig.
8.) dargestellt ist, und welche sich gegen das Ende des Laufes
vergroͤßerte; die Einbeugung wuchs uͤberdieß mit der Dike der
Wasserschichte, wie man in den Linien, fgh, f''g''h'', der Figur steht.
Es ist einleuchtend, daß diese Wirkungen dem Umstande zugeschrieben werden
muͤssen, daß noch von den Seiten her eine Zusammenziehung beim Austritte des
Wassers durch die Schleuse, jedoch eine innere und unmerkliche, Statt fand; dieses
wurde uns in der Folge bewiesen, wo wir, als diese Schleuse so eingerichtet war, wie
Fig. 5 und
6. zeigt,
und wie es unter N°. 18. erklaͤrt wurde,
durch den Versuch einsahen, daß, selbst fuͤr Wasser-Diken von 3 Cent., die
Seiten-Eindruͤkung nicht mehr Statt hatte, so daß der Durchschnitt der oberen
Flaͤche uͤberall eine vollkommen gerade Linie darboth.
42. Das oben (40) dargestellte Verfahren fuͤhrte uns dahin, die Zahl 0,85 fuͤr das
Verhaͤltniß der Flaͤchen-Raͤume des und der Oeffnung des
Schuzbrettes anzunehmen, indem man diesen Durchschnitten die gewoͤhnliche
Breite von 76 Mill. gab, welche auch dem Laufe zukommt. Diese Zahl ist, wie man
steht, groͤßer als jene, welche man fuͤr das Verhaͤltniß des
wirklichen und theoretischen Verbrauches erhielt; und man kann fuͤr ihre
Genauigkeit auf mehr denn ein oder zwei Hundertel nicht gut stehen, indem diese
Hundertel dort den Zehnteln eines Millimeters entsprechen; ein Grad von
Annaͤherung, welchen man sich nicht schmeicheln durfte, in dem Ergebnisse der
Masse erhalten zu haben.
Hiernach, und wenn man uͤberdieß die wirklichen Verbrauche und die Breite von
76 Mill., welche fuͤr den zusammengezogenen Durchschnitt angenommen wurden,
als genau voraus sezt, steht man, daß die Zahlen der 7ten Columne um einige
Hundertel von ihren wirklichen Werthen abweichen koͤnnen, und daß, in dem
gegenwaͤrtigen Falle, kein Beweis dafuͤr vorhanden ist, daß die
Geschwindigkeit am zusammengezogenen Durchschnitte wesentlich jener gleich sey,
welche durch die Theorie fuͤr die großen Hoͤhen des Wassers angezeigt
wurde; daß einzige Gewisse ist, daß der Fehler, wenn einer Statt hat, alle im
gleichem Verhaͤltnisse treffen muß. Die naͤhmlichen Bemerkungen lassen
sich auch auf die Zahlen der achten Columne anwenden; was jene der folgenden Columne
betrifft, welche die wichtigsten fuͤr den Zwek dieser Abhandlung sind, so
muͤssen die Fehler kleiner seyn, da sie von der Messung einer dichteren
Wasserschichte abhaͤngen. Nach der schon in N°. 36. gemachten Bemerkung haben wir Grund, zu glauben, daß dieser
Fehler nicht ein 40tel oder gar ein 50tel uͤbersteigt, und daß er nothwendig
dazu dient, den wahren Werth der Zahlen der 9ten Columne zu vergroͤßern.
43. Wie dem auch sey, diese Zahlen beweisen, daß, obschon die Geschwindigkeiten des
Wassers bei der Zusammenziehung auf der einen Seite in einem veraͤnderlichen
Verhaͤltnisse mit den theoretischen Geschwindigkeiten, und auf der anderen
Seite mit den Geschwindigkeiten unter dem Rade stehen, doch, durch eine Art von
Ersaz, diese lezteren sich in einem Verhaͤltnisse befinden, welches man fast
als bestaͤndig mit den theoretischen Geschwindigkeiten, d.h. mit jenen
Geschwindigkeiten betrachten kann, welche nach der Theorie der Hoͤhe des
Wassers uͤber der
Muͤndung zukommen; wirklich gehen die Differenzen der Zahlen der neunten
Columne nicht uͤber ein Tausendtel.
Diese Zahlen wurden, in der That, nur fuͤr 5 unter sich ziemlich entfernte
Ausdruͤke berechnet; da aber die Flaͤchenraͤume der
Durchschnitte des Wassers unter dem Rade ausnehmend wenig abaͤnderten, und
doch auf eine staͤtige Art gradweise abnahmen, so daß es leicht ward, sie
durch Beobachtung des Profiles zu bestaͤtigen; so war es nicht sehr
noͤthig, diesen Ausdruk kuͤrzer zu fassen, um mit
hinlaͤnglicher Genauigkeit das ihnen zukommende Gesez zu erhalten. Indem wir
uͤberdieß die Krumme zogen, welche dieses Gesez fuͤr die verschiedenen
Hoͤhen des Wassers darstellt, konnten wir neue Ausdruͤke zwischen die
ersten einschalten, und also zur Erkenntniß gelangen, daß die Zahlen der neunten
Columne, fuͤr die ganze Reihe der Versuche zwischen 0,848 und 0,858 blieben.
Man kann daher, in dem gegenwaͤrtigen Falle, den Verlust an Geschwindigkeit,
welchen das Wasser von Seite der verschiedenen Widerstaͤnde und inneren oder
aͤußeren Zusammenziehungen erleidet, als bestaͤndig betrachten; die
Zahl 0,854, als die mittlere unter allen der neunten Columne, kann uͤberdieß
fuͤr jene genommen werden, welche die Geschwindigkeiten, die, nach der
Theorie, den verschiedenen Hoͤhen des Wassers uͤber dem Mittelpuncte
der Muͤndung zukommen, multipliciren muß, und ihr Quadrat 0,729, welches ein
wenig zu stark (42) seyn muß, fuͤr die Zahl, womit man diese
naͤhmlichen Hoͤhen multipliciren muß, wenn man die Faͤlle
erhalten will, welche den wirklichen Geschwindigkeiten des Wassers am Rade
zukommen.
44. Nach diesen verschiedenen Betrachtungen, welche noͤthig waren, um den Zwek
der Tabelle in N°. 37. aufzuklaren, werden wir zu
den Versuchen uͤbergehen, welche die Oeffnungen des Schuzbrettes von 2 und 3
Cent. Hoͤhe betreffen; und zur Vermeidung unnuͤzer Wiederholungen
werden wir sie vereint, jedoch in zwei verschiedenen Tabellen, liefern.
Zweite Tabelle der Versuche
uͤber das Ausfließen des Wassers, wenn die Hoͤhe der Muͤndung 2
Cent. betraͤgt.
Nummern der Versuche.
Hoͤhe des Wassers uͤber dem Grunde des
Schuz-Brettes.
Wirklicher Verbrauch des Wassers in Litres.
Verbrauch nach der Theorie.
Verhaͤltnisse des wirklichen und theoretischen
Verbrauches, oder der Geschwindigkeiten am Schuz-Brette.
Geschwindigkeit des Wassers am Schuzbrette nach der
Theorie.
Verhaͤltnisse der wirklichen Geschwindigkeiten
am zusammengezogenen Durchschnitte zu den theoretischen
Geschwindigkeiten.
Verhaͤltnisse der wirklichen Geschwindigkeiten
am Rade und am zusammengezogenen Durchschnitte.
Verhaͤltnisse der Geschwindigkeiten unter dem
Rade zu den theoretischen Geschwindigkeiten.
m.
lit.
lit.
m.
1
0,269
2,746
3,426
0,801
2,254
0,971
0,944
0,917
2
0,252
2,726
3,379
0,807
2,179
0,978
0,950
0,929
3
0,212
2,413
3,026
0,797
1,991
0,966
0,962
0,929
4
0,192
2,300
2,872
0,801
1,889
0,971
0,964
0,936
5
0,184
2,244
2,807
0,799
1,847
0,968
0,967
0,936
6
0,172
2,140
2,710
0,790
1,783
0,958
0,971
0,930
7
0,142
1,927
2,446
0,788
1,609
0,955
0,977
0,933
8
0,117
1,735
2,202
0,787
1,449
0,954
0,985
0,939
9
0,102
1,586
2,042
0,777
1,343
0,942
1,004
0,946
10
0,082
1,368
1,806
0,757
1,188
0,917
1,020
0,935
11
0,072
1,227
1,676
0,732
1,103
0,887
1,038
0,921
Dritte und lezte Tabelle der Versuche
uͤber das Ausfließen des Wassers; Hoͤhe der Muͤndung 3
Cent.
Nummern der Versuche.
Hoͤhe des Wassers uͤber dem Grunde des
Schuz-Brettes.
Wirklicher Verbrauch des Wassers in Litres.
Verbrauch nach der Theorie.
Verhaͤltnisse des wirklichen und theoretischen
Verbrauchs oder der Geschwindigkeiten am Schuz-Brette.
Geschwindigkeit des Wassers am Schuzbrette nach der
Theorie.
Verhaͤltnisse der wirkl. Geschwindigkeiten am
zusammengezogen. Durchschnitte zu den theoret. Geschwindigkeiten.
Verhaͤltnisse der wirklichen Geschwindigkeiten
am Rade und am zusammengezogenen Durchschnitte.
Verhaͤltnisse der Geschwindigkeiten unter dem
Rade zu den theoretischen Geschwindigkeiten.
m.
lit.
lit.
m.
1
0,260
4,461
4,998
0,892
2,192
0,963
0,963
0,927
2
0,246
4,304
4,856
0,886
2,130
0,956
0,965
0,923
3
0,227
4,112
4,649
0,884
2,039
0,954
0,969
0,924
4
0,212
3,957
4,482
0,883
1,966
0,953
0,971
0,925
5
0,205
3,890
4,403
0,884
1,931
0,954
0,973
0,928
6
0,192
3,775
4,252
0,883
1,865
0,953
0,978
0,932
7
0,182
3,608
4,127
0,874
1,810
0,943
0,981
0,925
8
0,166
3,434
3,922
0,875
1,720
0,944
0,988
0,933
9
0,152
3,228
3,737
0,864
1,639
0,932
0,995
0,927
10
0,142
3,041
3,596
0,846
1,577
0,913
1,006
0,918
11
0,128
2,897
3,393
0,854
1,488
0,927
1,018
0,944
12
0,111
2,629
3,128
0,840
1,372
0,906
1,026
0,930
13
0,102
2,470
2,980
0,829
1,307
0,894
1,034
0,924
14
0,090
2,244
2,768
0,811
1,214
0,875
1,065
0,931
15
0,082
2,056
2,615
0,786
1,147
0,848
1,083
0,918
16
0,072
1,868
2,415
0,773
1,059
0,834
1,095
0,913
Bemerkungen.
45. Diese zwei Tabellen bestaͤtigen den groͤßten Theil der Bemerkungen,
welche uͤber die vorhergehende Tabelle gemacht wurden; die neunte Columne der
Tabelle N°. II. scheint immer anzuzeigen, daß das
Verhaͤltniß der wirklichen Geschwindigkeiten unter dem Rade zu den
theoretischen Geschwindigkeiten nicht fuͤr alle Hoͤhen des Wassers
bestaͤndig, und daß es fuͤr die Kleinen ein wenig groͤßer ist;
allein wir koͤnnen dieses Ergebniß nicht annehmen, indem die Versuche, welche
auf diese Tabelle sich beziehen, unter minder guͤnstigen Umstaͤnden,
als jene der zwei anderen, angestellt wurden, abgesehen davon, daß die Witterung
minder ruhig, und daß man gezwungen war, die Reihe der Versuche oft zu unterbrechen;
die mindesten Bewegungen der Luft reichen auch wirklich zu, um in Beobachtung des
Verbrauches oder der Ausfluͤsse des Wassers Differenzen zu geben, welche bis
auf 80, und selbst auf 60 Hundertel Cent. ihres Gesammt-Werthes steigen.
Wenn man uͤbrigens die Versuche 1, 8, 9 und 11. der Tabelle, nicht in Rechnung
bringt, deren Ergebnisse die groͤßten Unregelmaͤßigkeiten darbiethen,
so wird man hinlaͤnglich berechtigt seyn, die Zahlen der neunten Columne als
bestaͤndig zu betrachten, da ihre Differenzen nicht Ein Hundertel betragen;
wenn man daher die mittlere unter allen diesen Zahlen nimmt, wird man finden, daß
sie gleich ist 0,9255, deren Quadrat, wie wir schon (43) erklaͤrten, das
mittlere Verhaͤltniß der Hoͤhe, welche den wirklichen
Geschwindigkeiten des Wassers am Rade zukommt, zu den entsprechenden Hoͤhen
des Wassers im Behaͤlter ist, welche beim Austritte aus dem Mittelpuncte der
Muͤndung des Ausflusses genommen wurden.
46. Wenn man auf die naͤhmliche Weise die Zahlen der neunten Columne der
dritten Tabelle behandelt, und jene ausschließt, welche den Versuchen 10, 11, 15 und
16. entsprechen, welche offenbare Unregelmaͤßigkeiten darbiethen, so wird man
fuͤr das mittlere Verhaͤltniß der Geschwindigkeiten am Rade zu den
entsprechenden theoretischen Geschwindigkeiten, 0,9274, und fuͤr jenes der
Hoͤhen dieser Geschwindigkeiten 0,860 finden. Diese Zahlen sind, wie man
steht, nur in den Tausendteln von den vorhergehenden unterschieden, woruͤber
man beim ersten Anblike erstaunt seyn wird, indem die Differenz mit Yen
entsprechenden Zahlen,
welche fuͤr eine Oeffnung des Schuz-Brettes von 1 Cent, gefunden wurden, so
groß ist.
Wenn man indessen auf der einen Seite erwaͤgt, daß der Widerstand des Wassers
im aͤußeren Laufe mit der Groͤße des Durchschnittes abnehmen muß, und
daß, auf der anderen Seite, die Verluste an Geschwindigkeit durch den Widerstand und
die Zusammenziehungen im inneren Canale (18) mit der Oeffnung des Schuzbrettes
wachsen muͤssen, oder mit der Geschwindigkeit, welche das Wasser, bevor es
dorthin kommt, erlangt; so wird man ohne Muͤhe begreifen, daß, in gewissen
Faͤllen, sich diese beiden Wirkungen ergaͤnzen, welche nothwendig im
End-Ergebnisse beigefuͤgt werden muͤssen. Dieß ist uͤbrigens
klar genug durch die Columnen 7 und 8. unserer drei Tabellen angezeigt.
47. Ehe wir weiter gehen, bemerken wir, daß das bestaͤndige Verhaͤltniß
der Flaͤchenraͤume des zusammengezogenen Durchschnittes und der
Oeffnung des Schuzbrettes nach den mittleren Ergebnissen mehrerer Versuche, als
0,825 fuͤr den Fall der zweiten Tabelle, und als 0,927 fuͤr jenen der
dritten gefunden wurde; Zahlen, welche wir als etwas zu groß (36) betrachten, obwohl
die erste nicht um Ein und ein halbes Hundertel, und die zweite um Ein Hundertel von
ihrem wahren Werthe abweicht. Dieselbe Bemerkung gilt fuͤr die Zahlen der
Columnen 7, 8 und 9. der zwei lezteren Tabellen, und folglich fuͤr jene der
Artikel 45 und 46., die daraus abgeleitet sind. Die Ziffern der achten Columne
wurden uͤbrigens mit Huͤlfe von neun Profilen, die nahe am Rade
fuͤr die zweite Tabelle, und mit Huͤlfe von eilf aͤhnlichen
Profilen fuͤr die dritte angestellt wurden, erhalten.
Hierzu berechnete man anfangs die Verhaͤltnisse der
Flaͤchenraͤume dieser Profile zu jenem des zusammengezogenen
Durchschnittes; indem man dann diese Verhaͤltnisse als Ordinaten, und als
Abscissen die entsprechenden Wasserhoͤhen der zweiten Columne nahm,
construirte man eine Reihe von Puncten, durch welche man eine regelmaͤßige
und staͤtige Krumme zog, welche sich sehr wenig von diesen Puncten entfernt,
und also mit genuͤgender Genauigkeit das wahre Gesez der aus den Versuchen
hergeleiteten Verhaͤltnisse darstellte. Nach diesem Geseze wurden die Zahlen
der achten Columne der Tabellen berechnet; Zahlen, deren Werth nicht uͤber 6
Tausendtel von jenen des Versuches, fuͤr die Ausdruͤke, welche den verschiedenen Messungen
der Durchschnitte entsprechen, abweicht.
48. Die naͤhmliche Construction belehrte uns uͤberdieß, daß die
erhaltene Krumme sich aͤußerst wenig von einer gleichseitigen Hyperbel
unterschied; indem sie die Achse der Ordinaten zu einer ihrer Asymptoten, und eine
Parallele mit der Achse der Abscissen zur anderen Asymptote hat. Wenn man z.B. die
bestaͤndige Zahl, 0,91, von allen Zahlen der achten Columne der Tabelle N°. III. wegnimmt, und wenn man die verschienen
Reste mit den entsprechenden Hoͤhen des Wassers, welche in der zweiten
Columne angegeben sind, multiplicirt, so wird man finden, daß die auf diese Weise
erhaltenen Producte sich nicht um ein Zwanzigstel, unter oder uͤber, von
ihrem mittleren Werthe entfernen; so daß, wenn man diesen neuen mittleren Werth mit
den verschiedenen Hoͤhen der Faͤlle dividirt, und zum Quotienten die
bestaͤndige Zahl 0,91 addirt, die man anfangs weggenommen hatte, die Zahlen,
die sich daraus ergeben werden, von ihrer Seite nur in den Tausendteln sich von
jenen unterscheiden werden, welche ihnen respective in der achten Columne der
Tabelle entsprechen. Die naͤhmliche Bemerkung findet ihre Anwendung
fuͤr die Tabellen N°. I. und II.
Dieser Umstand, verbunden mit der Bemerkung, daß das Verhaͤltniß der
Geschwindigkeiten unter dem Rade zu den theoretischen Geschwindigkeiten, welches
durch die lezte Columne der Tabellen gegeben ist, bestaͤndig ist, erlaubt uns
die verschiedenen Ergebnisse unserer Versuche in allgemeinen Formeln
auszudruͤken. Hierzu nennen wir:
a, die Hoͤhe der Muͤndung oder Oeffnung
des Schuzbrettes;
b, seine Breite, und, s,
seinen Flaͤchenraum;
H, die Hoͤhe des Niveau's des Wassers
uͤber dem Grunde des Schuzbrettes;
h = H – a/2 die
Hoͤhe eben dieses Niveau's uͤber dem Mittelpuncte der
Muͤndung;
K, das Verhaͤltniß des wirklichen und
theoretischen Verbrauches oder Ausflusses.
DcDt diese respectiven Verbrauche;
Vt die Geschwindigkeit des Wassers, welche nach
der Theorie der Hoͤhe, h, zukommt;
Vt die mittlere wirkliche Geschwindigkeit des
Wassers am zusammengezogenen Durchschnitte;
Vr, die mittlere wirkliche Geschwindigkeit unter
dem Rade;
A, das bestaͤndige Verhaͤltniß dieser
lezteren Geschwindigkeit zur theoretischen Geschwindigkeit, ein Verhaͤltniß,
welches in der neunten Columne gegeben ist;
B, die bestaͤndige Groͤße, welche von den
Zahlen der achten Columne weggenommen ist, und welche so, wie das Product der Reste
in die Hoͤhen, H, welche durch die zweite Columne
gegeben sind, unveraͤnderlich ist;
C, endlich das unveraͤnderliche Product, um das
es sich handelt.
Nach dem Vorausgegangenen wird, wenn man wie gewoͤhnlich, die Schwere, g, nennt.
Textabbildung Bd. 19, S. 471
woraus, unter anderen:
Textabbildung Bd. 19, S. 471
Diese Formeln sind, durch gehoͤrige Bestimmung der bestaͤndigen darin
vorkommenden Großen, geeignet, die Werthe der Tabellen mit einer Genauigkeit
darzustellen, welche mit jener der Versuche selbst vergleichbar ist.
So hat man z.B. in dem Falle einer Oeffnung des Schuzbrettes von 0,03 Cent., (46, 47
und 48.)
S = 0m, 030.
0m, 076, s'
= 0m, 0278. 0m, 076, A =
0,927, B = 0,91, C =
0,01341.
Wenn man diese Werthe substituirt, wird
Textabbildung Bd. 19, S. 471
Formeln, welche die Zahlen der Columnen 5 und 3. der dritten
Tabelle bei weniger als einem Hundertel ihrer Werthe wieder geben.
49. Diese verschiedenen Formeln koͤnnen uͤbrigens nicht gerade hin auf
die gewoͤhnlichen Faͤlle der Praxis angewendet werden, indem die
bestaͤndigen Groͤßen, welche in ihnen vorkommen, unbekannte Functionen
verschiedener Daten sind, und die einzelnen angebrachten Vorrichtungen (18) nicht
angewendet werden muͤssen, da sie einen betraͤchtlichen Theil der
Geschwindigkeiten des Wassers beim Austritte aus der Schleuse verlieren machen. Wir
stellten dieselben nur auf, um einen Maßstab fuͤr die Genauigkeit zu liefern,
welche in den Versuchen erhalten wurde, und um das noͤthige Vertrauen in die
Ergebnisse, welche man daraus abzuleiten Willens ist, einzufloͤßen;
vielleicht dienen sie auch in der Folge irgend einen noch dunklen Punct in der
Theorie der Fluͤßigkeiten aufzuklaͤren. Man darf nicht vergessen, daß
unser wesentlicher Zwek hier ist, den Verlust an Geschwindigkeit zu bestimmen,
welchen das Wasser von Seite der verschiedenen Widerstaͤnde erlitt, die mit
dem gebrauchten Apparate verbunden waren. In der folgenden Abtheilung werden wir das
Verhaͤltniß der Quantitaͤt der Wirkung, die wesentlich dem Rade
uͤbertragen wird, gegen jene pruͤfen, welche das Wasser in dem
Augenblike, wo es zu wirken anfaͤngt, besizt, und wir werden alle Ursachen
eroͤrtern, welche auf die Ergebnisse Einfluß haben konnten, so daß keine
Ungewißheit uͤber den Grad des Vortheiles uͤbrig bleibt, welchen in
der Praxis die Raͤder, von denen die Rede ist, gewaͤhren
koͤnnen.
Vierter Theil. Untersuchung der Groͤße der
Wirkung, welche, in verschiedenen Faͤllen, die Raͤder mit krummen
Schaufeln geben.
50. Da uns die Resultate, welche wir im vorhergehenden Paragraphe erhielten, in den
Stand sezen, die Geschwindigkeiten, welche das Wasser in dem Augenblike besizt, wo
es auf das Rad wirkt, unmittelbar zu berechnen; so wuͤrde es leicht seyn,
daraus auf den Theil der Wirkung, den dieses mittheilt, zu schließen, indem man sich
der Zahlen bedient, die in der Tabelle des Artikels 30. eingetragen sind. Allein wir
haben uns vorgesezt, zuerst einige schwierige Puncte zu eroͤrtern, worauf wir
den Leser bereits aufmerksam gemacht haben.
Fuͤr's Erste hat man bemerkt (43 und 46.), daß die Verhaͤltnisse der
wirklichen Geschwindigkeiten des Wassers am Rade zu den Geschwindigkeiten, welche,
nach der Theorie, der Hoͤhe des Wassers unter dem Mittelpuncte der
Muͤndung zukommen, nach der Beschaffenheit der angewandten Operationen
vielleicht ein wenig zu hoch geschaͤzt wurden; nun geht daraus hervor, daß
die Quantitaͤten der Wirkung des Wassers, die aus diesen
Verhaͤltnissen abgeleitet werden, ebenfalls ein wenig groͤßer, als die
wahren, zu werden; der Fehler, wenn anders einer vorhanden ist, wird daher ganz zum Vortheile der
Schlußfolgen seyn, welche man in dieser Abhandlung aufzustellen suchte.
Zweitens haben wir auch bemerkt (33), daß, indem die lezteren Versuche weder zur
naͤhmlichen Zeit noch in demselben Locale mit jenen angestellt wurden, welche
die Messung der Quantitaͤt der vom Rade gelieferten Wirkung zum Gegenstande
hatten, die alten und neuen Ausfluͤsse oder Verbrauche nicht genau unter sich
uͤbereinstimmen koͤnnen. Dieß kann man wirklich durch Vergleichung der
drei lezten Tabellen mit jener des Artikels 30. sehen, in welcher die Verbrauche im
Allgemeinen schwacher sind, vorzuͤglich fuͤr die Oeffnungen des
Schuzbrettes von 3 Cent. Wir glauben, durch das Beispiel der
Unregelmaͤßigkeiten selbst, welche die Tabelle von N°. 30. darstellen, (31 und folg.) gezeigt zu haben, daß die
Differenzen nur in einem sehr geringen Grade den Fehlern zugeschrieben werden
koͤnnen, welche bei der wirklichen Messung der Verbrauche und der
Hoͤhen des Wassers begangen worden sind, und daß sie hauptsaͤchlich
davon herruͤhren, daß man nicht gewiß ist, in den verschiedenen
Faͤllen die naͤhmlichen Oeffnungen des Schuzbrettes erhalten zu haben,
indem es schwer haͤlt, diese Oeffnungen gehoͤrig zu bestimmen und zu
verhindern, daß sie nicht, nach einer bestimmten Zeit, durch verschiedene
Umstaͤnde sich aͤndern.
51. Endlich haben wir gleichfalls am Anfange des dritten Theiles bemerkt, daß die
Umstaͤnde des Ausfließens nicht auf eine merkliche Weise fuͤr die
naͤhmlichen Hoͤhen des Wassers und die Oeffnungen des Schuzbrettes,
welche man als gleich annahm, sich aͤndern mußten; so daß die
Geschwindigkeiten beinahe die naͤhmlichen in beiden Reihen der Versuche
geblieben waͤren, so wie die Verluste, welche sie von Seite der
Widerstaͤnde und Zusammenziehungen erleiden; wir koͤnnten daher die
Ergebnisse des dritten Theiles dieser Abhandlung unmittelbar zur Aufsuchung der
Quantitaͤten der Wirkung anwenden, welche das Wasser am Ende des Laufes
behaͤlt. Allein da, wenn man die Messung der Verbrauche in den verschiedenen
Faͤllen fuͤr genau annimmt, man versucht seyn koͤnnte, einen
Theil der Unregelmaͤßigkeiten auf die Veraͤnderung der
Geschwindigkeiten am Ausgange der Schleuse zu schieben, so ist es noͤthig,
den Einfluß zu pruͤfen, welcher von dieser lezteren Ursache herruͤhren
koͤnnte, unabhaͤngig von den Irrthuͤmern, welche in der
Schaͤzung der Groͤße der Muͤndungen begangen worden sind.
Weil nun die Versuche, welche die Tabelle des Artikels 30. betreffen, fuͤr die
naͤhmlichen Hoͤhen des Wassers und die als gleich angenommenen Muͤndungen,
im Allgemeinen groͤßere Verbrauche gegeben haben, als die ihnen in den drei
lezten Tabellen entsprechenden, so muß nothwendig die Geschwindigkeit am Eingange
des Laufes auch betraͤchtlich kleiner in den ersten Versuchen seyn, in Folge
der inneren Widerstaͤnde und der staͤrkeren Zusammenziehungen; allein,
die achten Columnen unserer drei lezten Tabellen, verglichen mit den dritten und
sechsten Columnen, beweisen, daß, wenn man in den naͤhmlichen Lauf zwei
Wasserschichten einbringt, von denen eine, eine betraͤchtlich groͤßere
Geschwindigkeit und Masse besizt als die andere, z.B. um einige Hundertel, die
Geschwindigkeiten, die respective am Ende des Laufes erhalten werden, auch unter
sich die naͤhmliche Ordnung der Groͤße nach befolgen werden, wie die
primitiven Geschwindigkeiten; daher ist man berechtigt, anzunehmen, daß die mittlere
Geschwindigkeit des Wassers unter dem Rade, wenn uͤbrigens alle
Umstaͤnde gleich waren, kleiner fuͤr die ersten Versuche, als
fuͤr die lezteren, seyn mußte; eine neue Folge, die vollkommen zu Gunsten der
Vorschlaͤge ausfaͤllt; welche wir fuͤr unser Rad aufzustellen
suchen, weil die in Tabelle (N°. 30.)
eingetragenen Verbrauche uͤberdieß genau sind, und weil die Schaͤzung
der Geschwindigkeiten unter dem Rade dazu dient, die Hoͤhen der
Faͤlle, und folglich die Quantitaͤten der Wirkung des Wassers zu
vergroͤßern.
52. Unter diesen Verhaͤltnissen also halten wir uns fuͤr berechtigt,
folgende Tabelle der Quantitaͤten der Wirkung des Rades, verglichen mit
jenen, welche das Wasser im Augenblike des Einwirkens besaß, aufzustellen; dieses
wird uͤberdieß a posteriori durch die
Regelmaͤßigkeit bewiesen werden, welche man in den Gesezen der Ergebnisse
beobachtet findet.
In dieser neuen Tabelle wurden die Zahlen der vierten Columne von jenen abgeleitet,
die ihnen in der dritten entsprechen, indem man sie respective mit den in den
Artikeln 43, 45 und 46. des dritten Theiles dieser Abhandlung bestimmten Zahlen
multiplicirte; daraus leiten sich ganz natuͤrlich die Geschwindigkeiten ab,
welche man in der folgenden Columne eingetragen findet. Was die Bildung der anderen
Columnen betrifft, so zeigt sie nach der Tabelle, die schon unter N°. 30. uͤber die Geschwindigkeiten und
Quantitaͤten der Wirkung des Rades aufgestellt wurde, keine weitere
Schwierigkeit.
Tabelle der Quantitaͤten der Wirkung und
Geschwindigkeiten des Wassers, fuͤr den Fall des Maximum's der Wirkung.
Textabbildung Bd. 19, S. 475
Nummern der Versuche; Hoͤhe
der Oeffnung des Schuzbrettes; Hoͤhe des Wassers uͤber dem Grunde
des Schuzbrettes; Hoͤhe der wirklichen Geschwindigkeit des Wassers unter
dem Rade; Wirkliche Geschwindigkeit des Wassers bei seinem Eintritte in das Rad;
Geschwindigkeit des aͤußeren Umkreises des Rades; Quantitaͤt der
wirklichen Wirkung des Wassers bei seinem Eintritte in das Rad;
Quantitaͤt des Maximums der Wirkung, welche das Rad liefert;
Verhaͤltniß zwischen der Quantitaͤt der Wirkung des Rades und
jener des Wassers
Bemerkungen.
Man steht aus den Zahlen der neunten Columne, daß das Verhaͤltniß der
Geschwindigkeit des aͤußeren Umkreises des Rades, fuͤr den Fall des
Maximum's der Wirkung, zur wirklichen Geschwindigkeit des Wassers in dem Augenblike,
wo es dort eintritt, sich nicht von der Zahl 0,50 entfernt, welche durch die Theorie
angegeben wurde: nur scheint sie im Allgemeinen etwas groͤßer zu seyn; man
muß aber bedenken, daß dieß nicht die Geschwindigkeit des aͤußeren Umkreises
des Rades ist, welche man haͤtte nehmen muͤssen, um mit ihr die
Geschwindigkeit des Wassers zu vergleichen, sondern jene des Umkreises, welcher dem
Mittelpuncte des mittleren Drukes dieses Wassers entspricht; was nothwendig die
Zahlen der neunten Columne verminderte. Ueberdieß hat die Bestimmung der
Geschwindigkeit, welche dem Maximum der Wirkung eigen ist, selbst eine zu große
Ungewißheit, als daß man die kleinen Differenzen, welche in der Tabelle bemerkt
sind, Fehlern der Beobachtung zuschreiben konnte. Unter diesem Gesichtspuncte also
findet sich die Theorie eben so gut erwiesen, als die verschiedenen Ergebnisse der
Versuche, welche man anstellte, um die Geschwindigkeit des Wassers im Laufe zu
messen.
54. Die zehnte Columne der Tabelle, welche das Verhaͤltniß der
Quantitaͤten der Wirkung des Rades und Wassers enthaͤlt,
gewaͤhrt das groͤßte Interesse in praktischer Hinsicht. Man steht
wirklich, daß dieses Verhaͤltniß nie unter 0,6 ist, waͤhrend es sich
in gewissen Faͤllen uͤber 0,75 erhebt da nun dieses Verhaͤltniß
bei den gewoͤhnlichen Schaufel-Raͤdern, nach Smeaton, im Durchschnitte
0,30 ist, so steht man, daß unser Rad unter den naͤmlichen Umstaͤnden
ein Ergebniß liefern wird, welches zwischen zwei und zwei, und ein halb Mahl des
Ergebnisses dieser lezteren Raͤder begriffen seyn wird, und welches nicht
sehr von dem Ergebnisse abweichen wird, welches die besten bekannten hydraulischen
Raͤder liefern. Wenn man sich uͤbrigens (13) erinnert, daß das Rad ein
bedeutendes Spiel im Laufe darboth, und wenn man bemerkt, daß der Verlust durch
dieses Spiel desto betraͤchtlicher wird, je kleiner das Volumen des Wassers
ist, so wird man sich zum Theile von der Verminderung Rechenschaft geben
koͤnnen, welche die Zahlen der zehnten Columne, fuͤr die kleinen
Oeffnungen des Schuzbrettes zeigen, wenn man sie mit jenen der groͤßeren
Oeffnungen vergleicht, welche den naͤmlichen Faͤllen
angehoͤren; so daß man Grund hat zu glauben, daß fuͤr ein besser
gebautes Rad die Ergebnisse weit staͤrker ausgefallen seyn
wuͤrden.
55) Man wird jedoch bemerken, daß fuͤr eine und dieselbe Oeffnung des
Schuzbrettes die Wirkung, welche das Rad mit krummen Schaufeln gibt, sich in dem
Maße etwas vermindert, als die Hoͤhe des Wassers in dem Behaͤlter,
oder die Geschwindigkeit im Laufe zunimmt! dieß haͤngt wahrscheinlich, davon
ab, daß der Verlust an Kraft durch den Widerstand des Wassers gegen die Krummen
selbst betraͤchtlicher wird: da aber auf der anderen Seite, dieser Verlust in
derselben Zeit abnehmen muß, als die Wassermasse zunimmt, so kann man mit Grunde
annehmen, daß die Ergebnisse im Großen fuͤr ein Rad der naͤmlichen Art
wenigstens eben so vortheilhaft seyn werden, wie im Kleinen; so daß man die Zahl
0,75 zur Darstellung des Verhaͤltnisses der Quantitaͤten der Wirkung,
welche das Rad und Wasser bei kleinen Faͤllen und starkem Verbrauche liefern,
annehmen kann; z.B. fuͤr Faͤlle unter 2 Fuß mit Oeffnungen des
Schuzbrettes von 15 bis 25 Cent. Hoͤhe; waͤhrend man fuͤr
dieses naͤmliche Verhaͤltniß in dem entgegengesezten Falle eines
großen Falles oder einer kleinen Oeffnung des Schuzbrettes nur die Zahl 0,65 sezen
kann.
Wenn man uͤbrigens das Spiel im Laufe in Rechnung bringen wollte, so
koͤnnte man, ohne sich sehr von der Wahrheit zu entfernen, die Zahl 0,80
fuͤr die kleinen, und 0,70 fuͤr die großen Geschwindigkeiten
nehmen.
56) Man wird sich bei diesen verschiedenen Gegenstaͤnden erinnern, daß bei der
eigenthuͤmlichen Beschaffenheit der Vorrichtung, welche wir gebraucht haben,
es uns unmoͤglich war, Versuche uͤber viel staͤrkere
Wasserhoͤhen, als 24 Centimetern, anzustellen, indem (8 und 13) das Wasser
dann aufgehoͤrt haben wuͤrde, auf das Rad die ganze Wirkung zu
aͤußern, deren es faͤhig ist. Wir verhehlen uns uͤbrigens
nicht, daß diese verschiedenen Ergebnisse durch Versuche, die mehr im Großen
angestellt werden muͤssen, bestaͤtigt werden wollen, und dieß nehmen
wir uns auch vor zu thun, sobald sich eine guͤnstige Gelegenheit dazu
darbiethen wird.
Da sich uͤberdieß diese Ergebnisse einzig auf die Quantitaͤten der
Wirkung des Rades beziehen, verglichen mit jenen absoluten des Wassers in dem
Augenblike, wo es auf dieses Rad wirkt, und da es in der Praxis sich oft zutraͤgt,
daß man sie mit den Quantitaͤten der Wirkung vergleicht, die dem ganzen Falle
des Wassers zukommen, welcher vom Niveau des Behaͤlters bis zum Grunde des
Rades reicht, so muͤssen wir die Sachen unter diesem lezteren Gesichtspuncte
pruͤfen.
57) Wir machten schon (18) bemerklich, daß man, durch eine schikliche Einrichtung des
Schuzbrettes und des Laufes unsers Apparates, leicht bewirken kann, daß das Wasser
beim Austritte aus der Schleuse eine Geschwindigkeit erlangt, welche jener gleich
ist, die ihm nach der Theorie zukommt, und keine merkliche Zusammenziehung an den
Seiten und dem Grunde des Laufes veranlaßt; es bleibt uns daher nur noch der Verlust
an Geschwindigkeit zu untersuchen, welcher allein durch die Reibung des Wassers
gegen die Waͤnde des Laufes verursacht werden kann.
Diese Frage wuͤrde ganz geloͤset seyn, wenn man mit Bossut annehmen
wollte, daß die Neigung von Einem Zehntel, die man dem Laufe gegeben, nothwendig
ist, um dem Wasser fortwaͤhrend den Verlust an Geschwindigkeit zu ersezen,
welchen es durch die Reibung erleidet; allein, man darf nicht vergessen, daß die
Versuche von Bossut sich nur auf Wasserschichten von 1 bis 2 Zoll Dike, bei 5 Zollen
Breite beziehen, bei Geschwindigkeiten, welche nie kleiner waren, als 2m,50, und auch nie bis auf 4 Meter stiegen: es scheint
aber aus vielen anderen Versuchen hervorzugehen, daß die Vergroͤßerung der
Wassermasse und die Verminderung der Geschwindigkeit derselben einen sehr großen
Einfluß auf die Schwaͤchung des Widerstandes durch die Reibung haben.
58) Die Betrachtung der achten Columnen der Tabellen der Artikel 37 und 44.
fuͤhrt zu einer aͤhnlichen Folge: denn die Zahlen dieser Columnen
zeigen deutlich, daß die Abnahme der Geschwindigkeit des Wassers, bei seinem
Durchgange quer durch den Lauf, um so viel geringer ist, als der Durchschnitt
groͤßer, und seine Geschwindigkeit schwaͤcher ist; man muß selbst
bemerken, daß das Gesez, das unter diesen Zahlen herrscht, fuͤr jede Oeffnung
des Schuzbrettes eine niedrigere Graͤnze bestimmt, die groß genug fuͤr
die Abnahme der Geschwindigkeit des Wassers im Laufe in Folge der
Widerstaͤnde ist; denn, wenn man z.B. H, oder die
Hoͤhe des Falles als unbegraͤnzt in der Formel des Artikels 48.
annimmt, welche diese Zahlen fuͤr eine Oeffnung des Schuzbrettes von 3 Cent.
darstellt, so wird man finden, daß diese Graͤnze 0,91 ist, d.h. daß die
Geschwindigkeit des Wassers am Ende des gebrauchten Laufes nie kleiner seyn wird,
als die 0,91 derjenigen, die am Eingange Statt hat.
59) Nach diesen verschiedenen Betrachtungen hat man Grund zu glauben, daß der Abhang
um Ein Zehntel nicht noͤthig ist, um dem Wasser die Geschwindigkeit zu
erstatten, welche es durch seine Reibung in dem Laufe erleidet, außer fuͤr
kleine Durchschnitte des Wassers und große Geschwindigkeiten; z.B. fuͤr
Durchschnitte unter 8 Cent. Tieft, bei 50 Cent. Weite, und bei Geschwindigkeiten
uͤber 4 Meter: in jedem anderen Falle wird der Abhang nothwendig geringer
seyn. Man steht wirklich taͤglich Leitungen, um das Wasser uͤber
Muͤhlen-Raͤder zu fuͤhren, deren Abhang nur ein Dreißigstel bei
Wasserschichten von 8 Cent. Tiefe, bei nur 50 Weite, und bei Geschwindigkeiten von 2
bis 4 Meter betragt, und in welchen doch diese Geschwindigkeit keinen bedeutenden
Verlust leidet, weil beinahe der naͤmliche Durchschnitt in der ganzen
Laͤnge des Canales bleibt: das Wesentliche ist, vor Allem die Zusammenziehung
am Eingange zu vermeiden.
Was die Oeffnungen des Schuzbrettes, oder die staͤrkeren Durchschnitte des
Wassers betrifft, z.B. von 15 bis 25 Cent. Hoͤhe bei wehr als 50 Weite; so
scheint aus einigen besonderen Beobachtungen hervorzugehen, daß man sich kaum
taͤuschen duͤrfte, wenn man den Abhang auf Ein Zwanzigstel
annaͤhme, im Falle die Geschwindigkeit nicht uͤber 6 M. stiege, oder
der Fall kleiner als 2 M. waͤre.
60) Wenn man diese gegebene Groͤße annimmt, so kann man, durch
Annaͤherung die Quantitaͤt der Wirkung berechnen, welche unserem Rade
in dem Falle, um welchen es sich hier handelt, wirklich uͤbertragen wird.
Wenn man uͤbrigens annimmt, daß, wenn das Schuzbrett, wie es die erste Figur
darstellt, geneigt, und auf eine Art eingerichtet ist, daß es die Zusammenziehung
(18) vermeidet, die Entfernung vom Fuße dieses Schuzbrettes bis zum senkrechten
Radius des Rades 1m,4 ist, was nur
fuͤr Raͤder von 5 bis 6m im
Durchmesser Statt finden wird, so wird die Hoͤhe des Abhanges, welche man
diesem Theile des Laufes zu geben hat, um dem Wasser seine urspuͤngliche
Geschwindigkeit zu erhalten, nach dem Vorausgehenden 7 Cent. seyn. Wenn man unter
obiger Voraussezung, nur einen Fall von 1m,50 uͤber dem Mittelpunkte der Muͤndung betrachtet, welche
selbst 20°
Hoͤhe haben wuͤrde; so wird man finden, daß der ganze Fall, vom Niveau
des Behaͤlters an bis unter das Rad, 1m,50 + 0m,10 + 0m,07 = 1m,67 seyn wird: da dieser Fall sich also auf 1m,50 reducirt findet, was eigentlich der
Geschwindigkeit des Wassers im Laufe zukommt; so wird die Quantitaͤt der
gegen das Rad verbrauchten Wirkung nicht mehr als 1,50/1,67 = 0,899 von derjenigen
seyn, welche dem ganzen Falle 1m,67
zusteht.
Wir haben gesehen (55), daß das Rad 0,75 dieser Quantitaͤt an Wirkung leisten
konnte; es wird sich also die Quantitaͤt der wirklich benuͤzten
Wirkung auf 075.0,899 = 0,674 zuruͤkgefuͤhrt finden, d.h. auf
ungefaͤhr 2/3 der Quantitaͤt der Wirkung, die dem ganzen Falle des
Wassers zukommt: ein Verhaͤltniß, das wahrscheinlich jenes, welches durch die
gewoͤhnlichen Eimer-Raͤder geliefert wuͤrde, in dem einzelnen
Falle, um den es sich hier handelt, uͤbertrifft, und welches, mit
groͤßerem Grunde, jenes der sogenannten Seitenraͤder
uͤbertrifft.
61) Wenn wir nun annehmen, daß, wenn uͤbrigens alle anderen Daten die
naͤmlichen bleiben, die Oeffnung des Schuzbrettes allein geaͤndert,
und auf 10 Cent. zuruͤkgefuͤhrt ist; so wird man durch
aͤhnliche Berechnungen, wie die vorhergehenden, und bei einem Abhange des
Laufes von Einem Zehntel, welcher auch hinlaͤnglich scheint, um dem Wasser
seine Geschwindigkeit zu erhalten, finden, daß die Quantitaͤt der
Geschwindigkeit, welche dem Wasser erhalten wird, 1,50/1,69 = 0,888 der
Quantitaͤt der Wirkung des ganzen Falles seyn wird; da nun das Rad nur 0,65
nach N°. 55. uͤbertraͤgt, so steht
man, daß der wirklich gebrauchte Theil 0,577 der Quantitaͤt der Wirkung seyn
wird, welche dem ganzen, Falle zukommt.
Die Verhaͤltnisse, welche man fand, wuͤrden uͤberdieß ein wenig
mit den Hoͤhen des Wassers im Behaͤlter zunehmen, weil der Einfluß der
Oeffnung der Schleuse schwaͤcher seyn wuͤrde: z.B. fuͤr die
Faͤlle von 2m wuͤrden sie
respective ungefaͤhr 0,7 und 0,6 werden: nichts destoweniger muß man diese
Zahlen als Graͤnzen betrachten, welche man nicht uͤberschreiten darf,
weil der Widerstand, den das Wasser in dem Laufe leidet, mit der Hoͤhe oder
Geschwindigkeit zunehmen muß.
62) Um ungefaͤhr zu sehen, was diese Zahlen bei kleinen Wasserhoͤhen im
Behaͤlter werden, z.B. bei Hoͤhen von 0,80; so bemerken wir, daß es
wahrscheinlich hinreichen wird, den Lauf bei einer Oeffnung des Schuzbrettes von
10c um Ein Zwanzigstel neigen, und um Ein
Dreißigstel bei einer Oeffnung von 20c und mehr; so daß
die Hoͤhe des Abhanges des Laufes ungefaͤhr 7c fuͤr den ersten Fall, und 5c
fuͤr den zweiten seyn wird: man wird also, wenn man nie vorher schließt,
finden, daß die Quantitaͤten der Wirkung, die das Rad respective liefert,
0,566 und 0,630 der Quantitaͤten der Wirkung des ganzen Falles seyn werden,
von dem Niveau des Wassers an, bis zum niedrigsten Puncte des Rades gerechnet.
63) Die vorausgehenden Ergebnisse duͤrfen nicht als sehr genau betrachtet
werden, sondern nur als der Wahrheit sich sehr annaͤhernd, und geeignet, den
respectiven Einfluß der Hoͤhe des Falles und der Oeffnung des Schuzbrettes
auf die Quantitaͤten der Wirkung, welche das Rad wirklich gibt, kennen zu
lehren: sie zeigen wirklich, daß es im Allgemeinen sehr vorteilhaft ist, der
Schleuse und dem Laufe eine nicht bedeutende Hoͤhe zu geben, und daß man sich
sehr huͤten muß, den Lauf auf Kosten dieser Hoͤhe zu erweitern, wie
man es oft bei den Raͤdern mit gewoͤhnlichen Schaufeln thut.
Wirklich kann im lezteren Falle der Verlust an Wirkung durch das Spiel des Rades und
durch den Widerstand, welchen das Wasser von Seite des Laufes leidet, durch den
Vortheil mehr als aufgewogen werden, welchen man durch Vermehrung der
Geschwindigkeit des Wassers bei seinem Austritte aus dem Behaͤlter hat, und
dadurch, daß man es auf einen kleinen Theil seiner Fluͤgel wirken
laͤßt, so daß der Druk vermehrt wird, welchen es ausuͤbt, indem es
laͤngs der Fluͤgel hinan steigt: bei den Raͤdern mit krummen
Schaufeln wuͤrde aber diese lezte Zunahme nie Statt finden.
Um sich ganz von dem Einfluße des Spieles des Rades in dem Laufe zu
uͤberzeugen, wann die bewegende Wasser-Schichte duͤnn ist, reicht die
Betrachtung hin, daß dieses Spiel im Allgemeinen 3c in
den hoͤlzernen Raͤdern, selbst wenn sie gut gebaut sind,
uͤbersteigt, was einen Verlust von ungefaͤhr 1/3 auf die
Quantitaͤt der ganzen Wirkung des Wassers verursacht, wann die Hoͤhe,
desselben im Laufe 10c ist; er wuͤrde sogar Ein
Sechstel fuͤr eine Wasserhoͤhe von 10 Cent. betragen; diese Bemerkung
ist sehr geeignet die Wichtigkeit schaͤzen zu lehren, das Spiel, worum es
sich hier handelt, bei den unterschlaͤchtigen Raͤdern so viel
moͤglich zu vermindern, und die Vortheile der gegossenen Raͤder, wenn
sie gut gebaut sind, vor den uͤbrigen zu zeigen.
64) Kurz, man wird sich nach allem dem, was vorausgeht, uͤberzeugen, daß,
fuͤr kleine Faͤlle, d.h. fuͤr Faͤlle, welche nicht 2
Meter uͤbersteigen, das Rad mit krummen Schaufeln Wirkungen gibt, welche sich
mit jenen der besten bekannten Raͤder vergleichen lassen, und jene der
Raͤder mit gewoͤhnlichen Schaufeln um vieles uͤbertreffen
werden, weil es unter den naͤmlichen Umstaͤnden eine Quantitaͤt
Wirkung geben kann, welche immer gewiß das Doppelte jener der lezteren seyn wird.
Seine Einfachheit, verbunden mit dem Umstande, daß es eine große Geschwindigkeit
gewaͤhrt, und uͤberall anwendbar ist, wird ihm ohne Zweifel einen
Vorzug vor den Seitenraͤdern in den meisten Faͤllen, und besonders in
jenen geben, wo die Faͤlle unter 2 M. sind, weil
es dann eine bedeutendere Wirkung erzeugen wird.Bei der Revision dieses Bogens erhalten wir das Dezemberheft der Annales de Chimie, in welchem Herr Poncelet noch einen berichtigenden Nachtrag zu
dieser Abhandlung lieferte, den auch wir im folgenden Hefte mittheilen und
hiemit unsere Leser darauf aufmerksam machen wollen. D.
Tafeln