| Titel: | Ueber die Theorie der parallelen Bewegung. Von J. R. Arris. |
| Fundstelle: | Band 35, Jahrgang 1830, Nr. LXXVIII., S. 332 |
| Download: | XML |
LXXVIII.
Ueber die Theorie der parallelen Bewegung. Von
J. R.
Arris.
Aus dem London Journal of Arts. November 1829. S.
61.
Mit Abbildungen auf Tab.
VIII.
Arris, uͤber die Theorie der parallelen
Bewegung.
Hr. Arris erklaͤrt, daß er mit Plumb's Bemerkungen im London
Journal of Arts
October, (Polyt. Journal
Bd. XXXV. S. 81.) einverstanden ist, wenn er
sagt: daß die Bahn der Staͤmpelstange einer Dampfmaschine dann einer geraden
Linie am naͤchsten kommt, wann die Laͤnge der Zaumstangen dem
Halbmesser gleich ist, oder der Entfernung der Hinteren Glieder von dem Mittelpunkte
des Balkens. Er wuͤnscht Folgendes eingeruͤkt zu sehen.
Ich will, sagt er, das Verhaͤltnis der Theile der parallelen Bewegung nach dem
aufgestellten Grundsaze geben, dasselbe aber zuerst in die Gestalt einer
geometrischen Aufgabe bringen, und mit jenem Falle, als Muster, beginnen, wo der
Halbmesser, oder die Entfernung der Hinteren Glieder von dem Mittelpunkte des
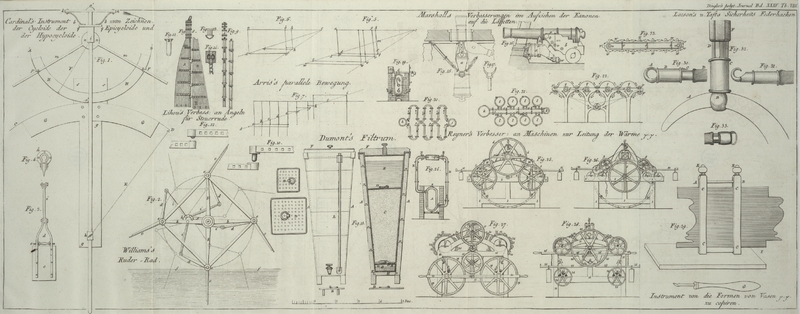
Balkens, gleich ist der Haͤlfte des großen Hebels, wie in Fig. 5., wo abc der große Hebel oder die Haͤlfte des
Balkens, c der Mittelpunkt, bf das Hintere Glied in der Mitte zwischen a
und c eingehaͤngt. In diesem Falle wird, wenn der
Balken sich in horizontaler Lage befindet, die Zaumstange, pq, mit der parallelen Stange, df, zusammenfallen. Wenn aber das Hintere Glied
unter irgend einem anderen Halbmesser aufgehaͤngt ist, werden sich sehr
leicht die Stellen der feststehenden Mittelpunkte der Zaumstangen auf folgende Weise
finden lassen.
Wenn der Balken in horizontaler Lage bleibt, fuͤhre man eine Linie von c durch d, und die Ebenen
der feststehenden Mittelpunkte der Zaumstangen werden irgendwo in dieser Linie sich
befinden. Man fuͤhre eine andere Linie von c
durch f, und die beweglichen Enden der Zaumstangen
werden sich irgendwo auf dieser Linie befinden. Ihre Ebenen lassen sich auf folgende
Weise finden.
Man seze die Hinteren Glieder haͤngen in g,
naͤher gegen das Ende a des Balkens. Man ziehe
eine Linie aus g parallel mit bf, und sie wird cf irgendwo durchschneiden, wie bei s. gs ist dann die Laͤnge des Hinteren
Gliedes. Man bringe dann das bewegliche Ende der Zaumstange (welches immer gleich
ist dem Halbmesser, oder der Entfernung des Hinteren Gliedes von dem Mittelpunkte)
auf das Ende s, des Hinteren Gliedes parallel mit af, so wird das andere Ende auf den Punkt r der Linie cd fallen.
Eben dieses Verfahrens kann man sich bei jeder anderen Lage der Hinteren Glieder
bedienen.
Ein Fall reicht hin, wann der Halbmesser des Hinteren Gliedes dem Mittelpunkte
naͤher als b ist (siehe Fig. 6), bei h. Man ziehe eine Linie von h parallel mit bf; sie wird die Linie
cf in k
durchschneiden. hk wird dann die Laͤnge des
Hinteren Gliedes seyn, und kl die Zaumstange, die
noch immer gleich ist dem Halbmesser h, c des Hinteren
Gliedes. In diesem Falle ist eine parallele Stange nothwendig, das Hintere Glied mit
dem Parallelogramme zu verbinden. Ich habe sie etwas hoͤher gestellt, damit
man sie desto deutlicher sieht.
Man mag nun irgend eine der Zaumstangen p, q, r, s, t, v, w,
x und ihrer correspondirenden Hinteren Glieder brauchen, so wird der Theil
des Punktes d immer identisch derselbe seyn. Zum Beweise
hiervon kann man ein Modell erbauen, an welchem alle Zaumstangen angebracht sind,
und alle ihre Hinteren Glieder so gestellt wie in Fig. 5., und man wird
finden, daß sie alle zugleich arbeiten koͤnnen.
Da die Laͤnge der Hinteren Glieder im Verhaͤltnisse zu ihrer Entfernung
von dem Mittelpunkte steht, so wird es leicht nach dem Geseze der
Verhaͤltnisse ihre Laͤngen auf folgende Weise zu finden. Wenn der
Halbmesser bc, Fig. 5., bf fordert als Laͤnge seines hinteren
Gliedes, was wird der Halbmesser gc fordern? Das
Resultat wird, gs, seyn, die Laͤnge seines
Hinteren Gliedes. Durch die kleine Zugabe zur Laͤnge der Hinteren Glieder
wird die Nothwendigkeit umgangen die Zaumstangen laͤnger zu machen, als ihren
Halbmesser oder die Entfernung vom Mittelpunkte.
Bei dieser Einrichtung sieht man, daß in dem aͤußersten Falle die Zaumstange
nie die Laͤnge des großen Hebels, abc,
uͤberschreiten kann, noch die Hinteren Glieder mehr als die Haͤlfte
der vorderen betragen koͤnnen.
Im Allgemeinen sind in der parallelen Bewegung nur zwei Punkte, die sich in
senkrechter Richtung bewegen, naͤmlich der Punkt d und der Punkt m in Fig. 5., wo
gewoͤhnlich die Luftpumpe aufgehaͤngt wird. Es kann aber jede
beliebige Anzahl derselben von einem Ende des Balkens zu dem anderen sich befinden
(siehe Fig.
7.), wenn sie nur alle auf den Linien cd
sind, und mit dem Parallelogramme verbunden sind, wie ab, cd, etc. und jenseits des
Mittelpunktes, bei i etc.
Tafeln