| Titel: | Beschreibung und Berechnung eines Regulators, welcher von den HHrn. Meyer und Comp. bei ihren Dampfmaschinen angewendet wird. |
| Fundstelle: | Band 94, Jahrgang 1844, Nr. LXXII., S. 329 |
| Download: | XML |
LXXII.
Beschreibung und Berechnung eines Regulators,
welcher von den HHrn. Meyer
und Comp. bei ihren Dampfmaschinen angewendet wird.
Im Auszug aus dem Bulletin de la Société
industrielle de Mulhouse 1844, Nr. 83.
Mit Abbildungen auf Tab.
V.
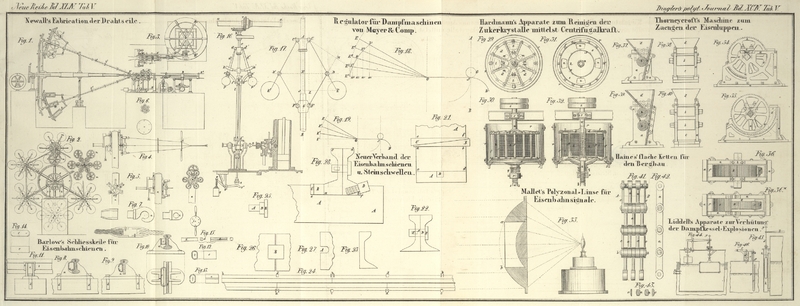
Beschreibung und Berechnung des Regulators für Dampfmaschinen von
Meyer und Comp.
Dieser Regulator wirkt auf ein Ventil, welches er während eines mehr oder weniger
großen Theiles des Kolbenlaufes offen erhält; das Ventil schließt sich dann, die
Communication zwischen dem Kessel und Cylinder ist vollkommen unterbrochen, und der
im Cylinder eingeschlossene Dampfwirkt während des übrigen Kolbenlaufes nur noch
durch Expansion. Wenn in Folge einer Abnahme des Widerstandes die Bewegung der
Dampfmaschine sich beschleunigt, entfernen sich die Kugeln, das Ventil bleibt nicht
mehr so lange offen, und es gelangt weniger Dampf in den Cylinder. Bei einer Zunahme
des Widerstandes oder einer Verminderung des Druks im Kessel findet das Gegentheil
statt. Der Dampf kommt hiebei immer mit seiner ursprünglichen Spannung im Cylinder
an, so wenig auch die Dampfmaschine belastet seyn mag, und es wird also seine ganze
Spannkraft benuzt.
In Fig. 16 ist
a, a die Schwungradwelle, b,
b eine starke senkrechte Stange, deren Achse mit der Schwungradwelle in
derselben senkrechten Ebene liegt. Die drehende Bewegung der Schwungradwelle wird
auf die Stange b, b durch zwei Kegelräder von
45°, r und r'
übertragen, wovon das eine auf der Welle a, a, das
andere auf b, b befestigt ist, so daß die
Drehungsgeschwindigkeit des Regulators derjenigen der Hauptwelle a, a immer gleich ist. c ist
eine auf der Welle b, b befestigte Hülse; sie ist mit
zwei Flügeln versehen, an denen mittelst Gelenken die Stangen d, d, d', d' der Kugeln p und p' befestigt sind, welche leztere sich
frei um Aufhängepunkte in der senkrechten Ebene bewegen können, die durch diese
Punkte und die Achse der Stange b, b geht. An den
Punkten e und e' der Stangen
d, d, d', d' sind zwei
Arme e, f e', f' angebracht,
deren Enden f, f' mittelst Gelenken ebenfalls an einer
Hülse i befestigt sind, welche frei auf der Achse b, b gleiten kann. Die Achsen aller dieser Stangen und
die Mittelpunkte der Kugeln liegen in derselben senkrechten Ebene, welche durch die
Achse der Stange b, b geht. k,
k' ist ein an den Enden mit Schlizen versehenes zweiarmiges, auf der
Regulatorwelle befestigtes Stük; der Zwek desselben ist, die Entfernung der Kugeln
zu beschränken und zu verhindern daß die Mechanismen durch Veränderungen in der
Geschwindigkeit der Dampfmaschine benachtheiligt werden. Die Hülse i ist mit zwei Vorsprüngen versehen, an welchen zwei
Stangen l (wovon man aber nur eine in der Zeichnung
sieht) angebracht sind, welche parallel mit der Achse b,
b hinabreichen und das Expansions-Excentricum mit der Hülse i verbinden. Das Expansions-Excentricum m ist ein Cylinder, welcher in seiner ganzen Länge mit
einem cylindrischen Loch versehen ist, dessen Durchmesser dem äußeren Durchmesser
der Welle b, b gleich ist. In der Büchse dieses
cylindrischen Lochs sind zwei Ruthen angebracht, welche zwei auf b, b befestigte Keile aufnehmen, so daß das Stük m, welches wir uneigentlich Excentricum nennen,
gezwungen ist die drehende Bewegung von b, b anzunehmen
und zu gleicher Zeit längs dieser Welle gleiten kann. Dieses Stük ist außerhalb mit
zwei krummen Hebedaumen versehen, welche eben so lang sind wie es selbst; diese
(nach einer Erzeugenden des Cylinders geformten) Hebedaumen sind oben breiter als
unten; sie wirken auf die Stange t des
Expansionsventils, um dasselbe zu öffnen, und halten es mehr oder weniger lange
offen, je nach der Höhe des Excentricums, welche von der Entfernung der Kugeln
abhängt. Unter dem Excentricum ist ein Ring n, worin
sich die Welle b, b frei drehen kann; derselbe ist mit
zwei Lappen versehen, in welchen zwei Stangen o (wovon
man aber nur eine in der Zeichnung sieht) befestigt sind, welche so geführt sind,
daß sie sich nur in einer verticalen Ebene bewegen können. Die unteren Enden der
Stangen o sind durch ein Stük verbunden, welches in
seiner Mitte und unten eine Rolle s trägt. Auf diese
Rolle stüzt sich das eine Ende v'' eines Hebels v, v', v'', welcher am Punkt
v' beweglich ist und an dessen anderem Ende v ein Gegengewicht q hängt.
Der Druk von lezterem pflanzt sich auf die Hülse i fort,
welche es zu heben trachtet. Dieses Gegengewicht unterstüzt die Centrifugalkraft, um
die Entfernung der Kugeln zu bewirken.
Berechnung des Regulators.
Fig. 17. A, B ist die Achse des Regulators, C, C' sind die Aufhängpunkte der Stangen C, E und C', E', an deren Enden die Kugeln sich befinden; F und F' sind die
Befestigungspunkte der Stäbe D, F und D', F', welche die
Verbindung der Hülse mit den Stangen der Kugeln herstellen. Um die Rechnung zu
vereinfachen, wollen wir das Gewicht der Stäbe FD,
F'
D', EC und E'C' unberüksichtigt lassen, und voraussezen,
daß
CD = DF = C
'D
' = D
'F
' = a
CE = C
'E
' = b
AC = A
'C
' = GF = G
'F
' = d
AG = h, und
FCE = ψ und g = 9,8088 Met. = 33 bayerische Fuß sey. In E und E' seyen die
Schwerpunkte der Kugeln, die gleiches Gewicht haben sollen, welches mit P bezeichnet werden soll; p
sey der durch das Gegengewicht am untern Hebel ausgeübte Druk, p' sey das Gewicht der unteren Hülse und der anderen
Stüke, denn Gewichte das Annähern der Kugeln bewirken.
Abgesehen von der Reibung werden sich im Zustand der gleichförmigen Bewegung der
Maschine folgende Kräfte das Gleichgewicht halten:
1) die Centrifugalkraft, welche das Entfernen der Kugeln bewirkt;
2) die Kraft p, welche dasselbe bewirkt;
3) die Gewichte der Kugeln oder 2 P;
4) die Gewichte p', welche das Annähern der Kugeln
hervorzubringen suchen.
Ad. 1. Man hat vor allem 2P/g
die Masse der Kugeln; wird ferner mit v die Winkelgeschwindigkeit eines Punktes bezeichnet, dessen Entfernung
von der Drehungsachse gleich der Einheit ist, und ist EJ = r, so hat man für die
Winkelgeschwindigkeit des Punktes E oder E'
vxr.
Die Wirkung der Centrifugalkraft ist mithin: (2P)/g v² r,
denn die Centrifugalkraft gleicht dem Producte aus der Masse
in das Quadrat der Geschwindigkeit, dividirt durch den Halbmesser des vom Punkt
beschriebenen Kreises.
Da nun diese Kraft die Stange C, E oder C', E' um C oder C' zu drehen sucht,
und zwar mit der Länge des Momentenarms CL = b cos. ψ, so hat man
(2P)/g
v² rb
cos. ψ
gleich dem Momente der Centrifugalkraft.
Nun ist aber r = JE =
JL + LE =
d + b sin. ψ, und
ist t die Dauer einer Umdrehung des Regulators, so
wird
v = (2π)/t, und daher
2P/g
v² rb
cos. ψ = (8π² b cos. ψ)/(gt²) (d + b sin. ψ) P.
Ad. 2. Was den Druk p
betrifft, so wirkt derselbe in der Richtung FC im
Punkte F, und läßt sich in zwei andere Kräfte zerlegen,
von welchen die eine senkrecht gegen AB und die
andere in der Richtung FD wirkt; die erstere
dieser beiden Kräfte wird wegen der fixen Achse AB
aufgehoben, leztere aber bewirkt das Entfernen der Kugeln, und ist gleich
P/cos
ψ.
Da nun ihr Hebelarm
CM = a sin. 2 ψ = 2 a sin. ψ cos.
ψ
ist, so ist das Moment von p
2 ap sin. ψ.
Ad. 3. Das Gewicht der Kugeln ist 2 P, und da jede in ihrem Schwerpunkte wirkt, so ist ihr
Hebelarm
EL = b
sin. ψ,
und mithin ihr Moment
2 bP sin. ψ
Ad. 4. Es ist leicht einzusehen, daß das Moment von p'
2 a p' sin.
ψ'
ist.
Die Gleichgewichtsbedingung wird mithin folgende seyn:
(8bπ² cos. ψ)/(gt²)
(d + b sin. ψ)
P + 2 ap sin. ψ
– 2 bP sin. ψ – 2 ap' sin. ψ =
0 (1)
Nun hat man aus
CF = h = 2a cos. ψ
cos. ψ = h/2a
und sin. ψ = 1/2a √(4a²
– h²)
folglich erhält man, wenn diese beiden lezten Werthe in (1)
substituirt werden und die Gleichung in Bezug auf p
gelöst wird:
Textabbildung Bd. 94, S. 332
woraus p bestimmt werden kann, so
bald alles übrige angegeben ist.
Zugleich ersieht man hieraus, daß mit der Zunahme von h
die Verminderung von p und mit der Abnahme von h die Zunahme von p
begründet ist, so lange t constant bleibt.
Aus der Gleichung (2) ersieht man, daß p positiv, negativ
oder Null werden kann, je nachdem der dritte Theil des zweiten Gliedes der Gleichung
größer, kleiner oder gleich der Summe der beiden ersten Theile wird. Im ersteren
Fall wird p zum Entfernen und im zweiten zum Annähern der
Kugeln beitragen. Jeder dieser drei Fälle kann durch den Werth von h hervorgehen, und zwar wird für den größten Werth von
h die Kraft p negativ
seyn, und kann nach und nach in Null und positive Werthe übergehen, wenn h kleiner wird. Von den im zweiten Gliede der Gleichung
(2) vorkommenden Größen sind alle constant bis auf h und
t. – Nimmt man p
so an, daß
Textabbildung Bd. 94, S. 333
wird, bestimmt hieraus p', und
substituirt seinen Werth in (2), so erhält man für angegebene Werthe von h = h₁, h = h₂ etc. auch die
entsprechende p₁, p₂ etc. für p.
Nimmt man nun die in D wirkende Reibung, welche F seyn soll in Betracht, so wird ihr Hebelarm ND = a sin. ψ
und daher ihr Moment pa
sin. ψ seyn.
Es sey nun t' = t/n die Dauer einer Umdrehung, worin n eine Zahl bedeutet, welche größer als 1 ist, so wird
die Gleichung (1) des Gleichgewichts übergehen in
(8π²b cos. ψ) . n
²/(gt²) (d
+ b sin. ψ) P + 2 ap sin. ψ – 2 bP
sin. ψ – 2 ap¹ sin. ψ – af sin.
ψ = 0 (A)
Eliminirt man p zwischen dieser Gleichung und (1), so
erhält man
Textabbildung Bd. 94, S. 333
und substituirt man hierin für sin.
ψ und cos. ψ die Werthe sin. ψ = 1/2a
√(4a' – h²) und cos. ψ = h/2a, so wird
Textabbildung Bd. 94, S. 333
Fig. 18. G ist die um ihren Mittelpunkt bewegliche Rolle, welche
längs AB sich bewegen kann, EOID ein um O
beweglicher Hebel, dessen Arme OI und OE den Winkel EOE' machen. Damit der Mittelpunkt von G in
der Verticalen AB bleibt, muß der Theil I, D des Arms O, I, D
Evolvente von dem Kreise seyn, dessen Halbmesser O: I
ist. Ein an O, E angehängtes Gewicht übt den variablen
Druk p aus, welcher constant bleiben kann, wenn sich
sein Hebelarm ändert. Es sey der ganze Lauf des Druks in vier gleiche Theile
getheilt, h₁, h₂, h₃, h₄, h₅ seyen die auf einander
folgende Werthe von h und p₁, p₂, p₃, p₄ und p₅ die correspondirenden von p; die Winkel, welche durch den Hebelarm O, E mit der Horizontalen OE' bildet, seyen EOE', E₁ OE', E₂ OE', OE', E₃ OE' und Null. Nennt man nun P' das Gegengewicht, und sezt OI = L, und ist l₁ der
Hebelarm von P', welches dem p = p₁ correspondirt, so ist
L p₁ = l₁ P', woraus l₁ = L . p₁/P' A sich ergibt. Trägt man l₁ von O aus auf OE', so daß Oa₁ = l₁ wird, errichtet sodann von
a₁ aus auf Oa₁ die Senkrechte a₁b₁, so wird in b₁ der Punkt seyn, wo das Gegengewicht angebracht werden muß.
Auf dieselbe Weise könnte man die Punkte b₂, b₃, b₄ und E' des Aufhängepunkts erhalten, wodurch man die Curve
b₁ b₂ b₃ b₄ b₅ erhält, auf welcher dieser bleiben muß. In den
meisten Fällen begnügen wir uns, das Gewicht P' am Ende
des Hebels anzuhängen; alsdann verändert sich der Hebelarm nach dem Cosinus des
Winkels, welchen derselbe mit der Horizontalen bildet.
Fig. 19. Es
sey EO die Lage des Hebels, wenn sich der Drüker
oder das Röllchen am tiefsten Punkte seines Laufes oder Hubes befindet, E₁ O seine der Mitte
des Hubes des Drükers entsprechende Lage, endlich E¹O seine Lage, wenn der Drüker am
höchsten Punkt seines Hubs angelangt ist.
Sezen wir E¹ OF = α, E₁ OF = β und EOF = γ: so
erhalten wir Zur Bestimmung dieser Winkel die Relationen
P¹ l
cos. α = p₃ L,
P¹ l
cos. β = p₂ L,
P¹ l
cos. γ = p₁ L;
woraus sich ergibt
cos. β/cos. α = p₂/p₃ und cos.
γ/cos α = p₁ /p₃
und endlich
cos. β = p₂/p₃ cos. α und cos.
γ = p₁ /p₃ cos α.
Man gibt dem Winkel α einen gewissen Werth und
leitet daraus die Werthe für β und γ ab. Beinahe immer kann man durch Probiren einen
Werth für α ermitteln, so daß β – α
(γ – α)/2 ist, und dieses ist alsdann der passende Werth.
Es sey nun α¹ der auf diese Weise bestimmte
Winkel EOE¹, so handelt es sich um die
Bestimmung des Werths von L. Dieser muß so beschaffen
seyn, daß der mit diesem Halbmesser beschriebene und dem Winkel α¹ entsprechende Bogen der Länge des Laufs
des Excentricums gleich kommt. Bezeichnet n die Anzahl
der Grade von α¹, so ergibt sich der Werth
für L aus der Gleichung
L = (z
× 360)/2πn).
Ist einmal der Werth für L ermittelt, so ist es leicht,
eine der beiden Größen P¹ und l zu bestimmen.
Aus der vorhergehenden Entwiklung geht hervor, daß man immer einen Regulator mit
Schwungkugeln so construiren kann, daß die Geschwindigkeit der Maschine sich gleich
bleibt, wie groß auch im Zustand des Gleichgewichts die Entfernung der Kugeln seyn
möge, und daß die Entfernung oder die Annäherung der Kugeln für eine Geschwindigkeit
stattfindet, die von der normalen Geschwindigkeit um eine so geringe Größe als man
nur will differirt, ohne daß jedoch diese Differenz Null werden kann.
Wir bemerken übrigens, daß ein sehr empfindlicher Regulator, d.h. ein solcher, bei
welchem die Schwungkugeln für einen sehr geringen Unterschied in der Geschwindigkeit
der Maschine sich von einander entfernen oder einander nähern würden, in der Praxis
ein schlechter Apparat wäre, wenigstens für den Fall, daß dem Schwungrad die
geeigneten Verhältnisse abgehen sollten. Das Gewicht des Schwungrads wird in der
That, wie man weiß, so bestimmt, daß die extremen Geschwindigkeiten von der
mittleren Geschwindigkeit um 1/20 bis 1/60 der lezteren differiren. Wäre nun der
Regulator für eine geringere Abweichung der Geschwindigkeit empfindlich, als
diejenige, welche das Schwungrad gestattet, so würde er beständig spielen, und einen
dem beabsichtigten entgegengesezten Erfolg hervorbringen.
Die HHrn. J. Meyer und Comp.
besizen mehrere Modelle von Regulatoren, weil der Regulator bei ihren Maschinen
immer dieselbe Geschwindigkeit wie die Schwungradwelle hat, und diese
Geschwindigkeit bei jeder Maschine sich ändert; es ist übrigens gut, wenn die
Dimensionen des Regulators den Verhältnissen der Maschine, an welcher derselbe
angebracht ist, angemessen sind.
Bei Maschinen, deren Regulator über einem Ventile spielt, könnte man, streng
genommen, einen einzigen Regulator construiren, welcher auf alle Maschinen von was
immer für einer Kraft paßte; es genügte, die Transmission der Bewegung dergestalt
anzuordnen, daß die der Normalgeschwindigkeit der Maschine entsprechende
Geschwindigkeit des Regulators sich beständig gleich bliebe, wie beschaffen auch
diese Normalgeschwindigkeit wäre.
Man kann mit dieser Anordnung die normale Geschwindigkeit der Maschine nach Belieben
ändern, ohne dadurch einen merkbaren Unterschied in der Regelmäßigkeit der Bewegung
herbeizuführen, wenn nur diese neue Geschwindigkeit nicht allzuweit von der ersteren
abweicht. Zur Erreichung dieses Zweks genügt es, das Gegengewicht zu vermindern oder
zu vermehren, je nachdem man eine größere oder kleinere Geschwindigkeit wünscht.
Wollte man aber die Normalgeschwindigkeit der Maschine bedeutender, z.B. um 4 oder 5 Umdrehungen per Minute ändern, so würde eine Aenderung der
Gegengewichte zur Erhaltung einer genügenden Regelmäßigkeit nicht mehr hinreichen;
man müßte alsdann auch den Hebel ändern – ein Fall, der jedoch im Bereiche
der Industrie selten vorkommt.
Tafeln