| Titel: | Beschreibung und Anwendung des Goniograph von Collardeau. |
| Fundstelle: | Band 117, Jahrgang 1850, Nr. XXXIX., S. 197 |
| Download: | XML |
XXXIX.
Beschreibung und Anwendung des Goniograph von
Collardeau.
Aus dem Bulletin de la Société d'Encouragement, Jan.
1850, S. 34.
Mit einer Abbildung auf Tab. III.
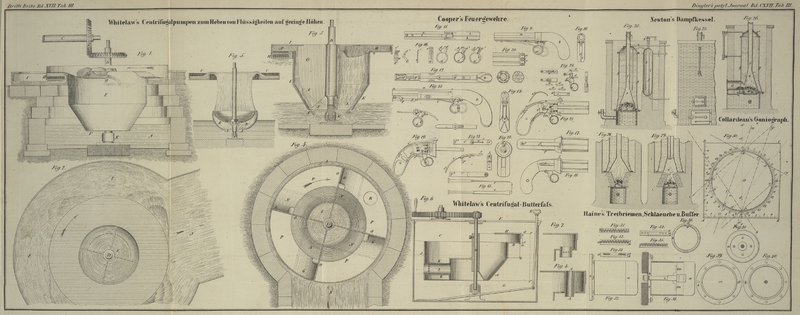
Collardeau's Goniograph.
Dieses Instrument ist in Fig. 30 dargestellt.
A B C D ist eine quadratische Messingplatte von einem
Decimeter Seitenlänge, aus deren Mitte ein Kreis b d
p′ a′ ausgedreht ist, welcher genau
gleichen Abstand von den Seiten und von den Winkeln des Quadrates A B C D hat.
Der Umfang dieses Kreises ist, von dem Durchmesser b
p′ angefangen, welcher parallel zu den Seiten A
D und B C des Quadrates liegt, in Grade
getheilt. Die Gradnummern auf jedem der beiden Halbkreise b d
p′, p′ a′ b laufen in der nämlichen Richtung
von 0 bis 180° fort, so daß zwei Punkte der Peripherie, die gleiche Nummern
haben, sich in einem und demselben Durchmesser befinden. Der Durchmesser, welcher
durch die Theilpunkte 90° geht, ist also parallel zu den Seiten A B und C D des
Instrumentes. Die Seiten A B und A D, welche den Winkel A des Quadrates A B C D einschließen, sind endlich noch jede in 100
Millimeter eingetheilt, die von 10 zu 10 numerirt sind, und zwar so, daß der
Nullpunkt der Theilungen mit dem Punkte A
zusammenfällt.
Die zwei Hauptprobleme, für welche das Instrument bestimmt ist, werden auf folgende
Weise gelöst.
Erstes Problem. Den Winkel abzumessen, welchen zwei gerade
Linien auf einem Plane einschließen.
Zur Lösung dieser Aufgabe kann man auf zweierlei Weise verfahren, wovon die erste
folgende ist: den Durchmesser, auf welchem sich die beiden Nullpunkte der Theilung
befinden, legt man an eine der zwei gegebenen Geraden an, und wenn in dieser Lage
der Kreis des Instrumentes die zweite Gerade nicht trifft, so verschiebt man
dasselbe einem Lineal entlang, das man vorläufig schon an eine der Quadratseiten
angelegt hatte, oder man kann nöthigenfalls das Instrument auch noch senkrecht auf
die vorige Richtung verschieben, wenn man das Lineal an eine anstoßende Seite
angelegt hat. Auf diese Weise wird man immer von der erstern Geraden auf die zweite
übergehen können, welches Stück der letztern auch gezeichnet seyn oder welche Lage
sie haben mag.
Ist dieß geschehen, und schneidet die zweite Gerade a′ a einen der Halbkreise des Goniographen,
z. B. den Halbkreis b
a′ p′ in den
Punkten a a′, so wird der abzumessende Winkel a′ a p′ als
Maaß die Hälfte des Bogens p′ c′ a′ weniger
den Bogen b a haben. Diese Bogen haben aber als
respective Werthe n und (180° - n′) Grade, wobei die Zahlen n und n′ den
Durchschnittspunkten a′ a der zweiten Geraden entsprechen. Der zu messende Winkel wird deßhalb als
Maaß Textabbildung Bd. 117, S. 198 oder n + n′/2 - 90° haben. Geht die zweite Gerade b b′ durch einen der Nullpunkte der Theilung, z. B. durch b, so ist der Winkel b′b p′ = dem durch die beiden
gegebenen Linien eingeschlossenen Winkel, und sein Maaß wird die Hälfte des Bogens
p′ c′ b′ seyn, oder die Hälfte der Zahl n von Geraden, welche zwischen o und b′, dem Durchgangspunkte der
zweiten geraden Linie, liegen, also n/2.
Schneidet die zweite Gerade d d′ die beiden
Umfanghälften des Goniographen, so sind die Scheitelwinkel d′ d, p′ und b d′ d gleich dem zu messenden Winkel, und da sie als Maaß die halbe Summe der
Bogen p′ d′
und b d haben, welche sie einschließen und welche durch
die Gradzahlen n, n′ ausgedrückt sind, die den
Durchgangspunkten d′ d entsprechen, so folgt daraus, daß der gesuchte Winkel gleich ist n + n′/2 oder der
halben Summe der Grade, welche zwischen 0 und den Durchschnittspunkten der zweiten
geraden Linie auf dem Instrumente liegen.
Falls die beiden Zahlen n, n′ die nämlichen sind,
drückt jede derselben den Werth des zu messenden Winkels in Graden aus, wobei dann
die zweite Gerade mit einem Durchmesser des Instrumentes zusammenfällt und durch die
Mitte 0 desselben geht.
Die zweite Art das Problem zu lösen, ist in dem Falle passend, wo der Goniograph auf
einmal an beiden Linien angelegt werden kann, was bei jeder Größe des Instrumentes
dann geschehen kann, wenn der Durchschnittspunkt der beiden Geraden nicht weit von
den gezeichneten Stücken der Geraden entfernt liegt.
Diese zweite Art besteht darin, daß man die beiden Nullpunkte der Theilung auf zwei
Punkte der beiden Geraden bringt, welche den zu messenden Winkel einschließen.
Ist der zu messende Winkel q r ein spitzer, so fällt der
Scheitel q desselben außerhalb des
Goniographen-Kreises, während die Schenkel p q
und r g durch die Nullpunkte b und p′ gehen.
Im Falle die zweiten Durchschnittspunkte p′ a′ der Schenkel mit dem getheilten Kreise des
Instrumentes nicht in eine Hälfte desselben fallen, so sieht man, daß wenn man mit
n und n′ die
Anzahl der Grade bezeichnet, die diesen Punkten entsprechen, der Werth des gesuchten
Winkels n - n′/2
Grade beträgt; dieß ist die halbe Differenz der Gradzahlen, die zwischen den nicht
mit den Nullpunkten zusammenfallenden Durchschnittspunkten der geraden Linien
liegen.
Wäre der Goniograph so gelegt, daß die beiden Schenkel p′ v, b v des
spitzen Winkels p′ v
b, die durch die Nullpunkte b und p′ gehen, eine und dieselbe Hälfte des
Instrumentes b d e p ′ schneiden, und zwar in den
Punkten e und d, die n und n′ Graden
entsprechen, so wäre das Maaß des zu messenden Winkels die Hälfte der Differenz
zwischen dem Halbkreise a a′ p′ und dem Bogen d e,
oder 90° - n - n′/2, das heißt ein rechter Winkel, weniger der halben Differenz der
Gradzahlen, welche durch die beiden Geraden auf ein und demselben Halbkreise des
Instrumentes abgeschnitten wurden.
Ist der zu messende Winkel s t u ein stumpfer, so
befindet sich der Scheitel t desselben innerhalb des
Goniographen-Kreises, während die Schenkel s t
und u t durch die Nullpunkte p′ und b gehen. Die verlängerten
Schenkel schneiden dann den dem Scheitel zunächst liegendem Halbkreis in den Punkten
s′ und c′,
welchen Punkten die Zahlen n und n′ entsprechen. Der stumpfe Winkel s t
u hat deßhalb als Maaß den Halbkreis b d
p′ und die Hälfte des Bogens c′ b′ s′, der n - n′ Graden gleich
ist, das heißt 90° + n - n′/2, oder einen rechten Winkel plus
der halben Differenz der Gradzahlen, die bei den Durchschnittspunkten mit den
geraden Linien stehen.
Fiele der Scheitel des zu messenden Winkels auf den Kreisumfang selbst, während die
Schenkel durch die Nullpunkte gehen, so wäre der Winkel ein rechter.
Zweites Problem. Durch einen gegebenen Punkt auf einer
Geraden oder außerhalb ihrer Richtung sey eine zweite Gerade unter irgend einem
bestimmten Winkel zu ziehen.
Die Lösung dieses Problems gründet sich auf das Vorhergehende; denn es wird, um den
Zweck zu erreichen, hinreichen, den Goniographen an die gegebene Linie so anzulegen,
daß die auf der gegebenen Geraden liegenden Gradnummern dem zu construirenden Winkel entsprechen. Die durch
die Nullpunkte des Instrumentes gezogene Gerade wird dann die verlangte Neigung
haben. Da nun die Seiten des Quadrates parallel zu dem die Nullpunkte enthaltenden
Durchmesser sind, so sind sie auch parallel zu der zu ziehenden Linie, und da man
mittelst der zwei auf einander senkrechten Bewegungen an einem Lineal den
Goniographen überall hin verschieben kann, so ist es immer möglich, eine Seite
desselben zu dem gegebenen Punkte zu bringen, und so eine gerade Linie zu ziehen,
welche unter dem verlangten Winkel durch den gegebenen Punkt geht.
Tafeln