| Titel: | Das Verhältniß des goldnen Schnitts in seiner Bedeutung für bildende Künstler und Techniker. |
| Fundstelle: | Band 137, Jahrgang 1855, Nr. LXXXIII., S. 322 |
| Download: | XML |
LXXXIII.
Das Verhältniß des goldnen Schnitts in seiner
Bedeutung für bildende Künstler und Techniker.
Mit einer Abbildung auf Tab. V.
Das Verhältniß des goldnen Schnitts in seiner Bedeutung für
bildende Künstler und Techniker.
Sobald der bildende Künstler oder Techniker irgend ein aus mehreren Theilen und
verschiedenen Dimensionen bestehendes Werk herzustellen hat, das nicht bloß dem
praktischen Bedürfniß genügen, sondern zugleich das ästhetische Gefühl befriedigen
soll, ist in formeller Beziehung keine Frage so wichtig für ihn, als die, welches
Größenverhältniß zwischen den einzelnen Theilen und Dimensionen bestehen müsse, um
das Werk als ein harmonisch gegliedertes, planmäßig geordnetes, kurz wohlgeformtes
Ganzes erscheinen zu lassen und dadurch auf das Auge wie auf den Geist des
Schauenden einen wohlgefälligen Eindruck zu machen. Soll das Werk die Nachbildung
irgend eines Naturerzeugnisses, z.B. eines menschlichen oder thierischen Körpers
seyn, so sind die innezuhaltenden Verhältnisse und die daraus hervorgehenden Formen
dem Bildner zwar im Allgemeinen vorgeschrieben, jedoch nicht so, daß er sich ohne
Selbstthätigkeit einer sklavischen Nachahmung überlassen dürfte: denn die Natur
producirt innerhalb einer und derselben Gattung sehr verschiedene und zwar nicht
bloß mehr oder minder schöne, sondern auch entschieden häßliche Gebilde; überhaupt
findet sich unter den Naturproducten keines, welches alle Vorzüge und Schönheiten
der Gattung in sich vereinigte und daher als allgemein gültiges Muster derselben
angesehen werden könnte; der Künstler muß sich also aus verschiedenen Einzelgebilden
der Natur selbst sein Ideal construiren, und es entsteht also auch in diesem Falle
für ihn die Frage, welche unter den verschiedenen von ihm beobachteten Verhältnissen
und Formen er gerade diesem Mustergebilde geben soll.
Noch schwieriger ist die Frage über die Wohlgefälligkeit der Verhältnisse für
diejenigen Bildner, welche Werke zu schaffen haben, zu denen sich in der Natur gar keine,
oder nur ganz rohe Vorbilder finden lassen, z.B. ein Gebäude, ein Hausgeräth, ein
Gefäß, ein Werkzeug, ein Gewand, ein Schmuck und dergl. Allerdings sind bis zu einem
gewissen Grade die Grundtypen der Formen und Verhältnisse auch hier durch die
Rücksicht auf den praktischen Zweck des Gebildes vorgezeichnet; aber die hieraus
resultirenden Bedingungen sind doch durchgängig nur so ganz allgemeine und
unbestimmte, daß sie sich ebensowohl ohne, als mit Befriedigung des Schönheitssinnes erfüllen lassen,
und der Künstler wird sich also diejenigen Regeln und Normen, die ihn in
ästhetischer Hinsicht zu leiten haben, selbst schaffen müssen.
Aus diesen Gründen haben die bildenden Künstler und die sich ihnen anschließenden
Techniker von jeher nach einem mehr oder minder gemeingültigem Proportionalgesetz
als sicherem Anhalt für das sehr bedeutenden Schwankungen und Irrthümern ausgesetzte
Gefühl gesucht; und indem man hiebei von der richtigen Ansicht ausging, daß der
menschliche Körper als das schönste der Naturgebilde auch die schönsten Verhältnisse
haben und daher als allgemeines Vorbild auch für andere Erzeugnisse benutzt werden
müsse, richtete man hauptsächlich sein Augenmerk darauf, zu erforschen, welche Verhältnisse des menschlichen Körpers unter der
unendlichen Masse der in der Wirklichkeit vorkommenden gerade als die idealen und
normalen anzusehen und in der Kunst anzuwenden seyen. Mit der Auffindung eines
solchen Kanons haben sich von den ältesten bis auf die neuesten Zeiten die
namhaftesten Vertreter der Kunst und Wissenschaft, wie Plato,
Polyklet, Vitruv, Leonardo da Vinci, Michel Angelo, Albrecht Dürer, Jean Cousin,
Audran, Winckelmann, Raphael Mengs, Schadow, Quetelet, Carus etc.
beschäftigt; aber so Treffliches auch in verschiedenen Beziehungen hiebei geleistet
worden ist, so gelang es doch nicht, ein Verhältniß zu entdecken, welches als
Normalverhältniß für die ganze Gliederung des Körpers hätte angenommen werden
können: denn indem man das Maaß irgend eines einzelnen Gliedes oder Abschnitts, z.B.
die Kopflänge, Gesichtslänge, Handlänge, Fußlänge, Nasenlänge etc. als Maaßeinheit
oder Modul annahm, fand man, daß die übrigen Glieder oder Abschnitte bald mehr, bald
weniger solcher Einheiten enthielten, und welches Maaß man auch als Modul ansehen
mochte: es blieben stets sehr viele und sehr wesentliche Abschnitte übrig, die zu
demselben durchaus nicht in einem rationalen, einfachen und übersichtlichen
Verhältnisse standen, und noch weniger ließ sich in der Anordnung und
Zusammensetzung dieser verschiedenen Abschnitte irgend ein einheitlicher Plan
entdecken, welcher den harmonischen Eindruck, den der Bau des menschlichen Körpers
unbestreitbar auf das unmittelbare Gefühl macht, auch nur einigermaßen für den Verstand und
für das wissenschaftliche Bedürfniß zu erklären im Stande gewesen wäre. Nur so viel
erkannte man und darin traf man von allen Seiten zusammen, daß jene Harmonie auf
einer Uebereinstimmung der Verhältnisse theils der einzelnen
Theile unter sich, theils der Theile zum Ganzen beruhen müsse, einen
wirklich in Zahl und Maaß auszudrückenden und dadurch praktisch brauchbaren Nachweis
dieser Uebereinstimmung wußte man jedoch nicht zu geben, und diese in ihrer
Allgemeinheit richtige Erkenntniß blieb also zufolge ihrer Unbestimmtheit eine für
Theorie und Praxis gleich sehr unbefriedigende.
Durch ästhetische Studien auf diese Lücke in der Kunstwissenschaft aufmerksam
geworden, machte ich diese Frage zu einem Gegenstande sorgfältigen Beobachtens und
Nachdenkens, und so ist es mir geglückt, das in Zahl und Maaß ausdrückbare
Verhältniß des goldnen Schnitts als dasjenige zu
entdecken, welches genau den Bedingungen der eben erwähnten Erkenntniß entspricht
und nach welchem in der That die menschliche Gestalt nach allen ihren Abschnitten
und Dimensionen gegliedert ist. Bekanntlich wird durch den goldnen Schnitt eine als
Ganzes gegebene Größe dergestalt in zwei ungleiche Theile getheilt, daß sich der kleinere Theil oder Minor (m) zum größern Theil oder
Major (M) eben so
verhält, wie der größere Theil zum Ganzen (T).
Es springt also in die Augen, daß in einem nach diesem Verhältniß eingetheilten
Gebilde wirklich die oben geforderte Uebereinstimmung der Verhältnisse theils der
Theile unter einander, theils der Theile zum Ganzen stattfindet: denn das Verhältniß
zwischen dem kleinern und größern Theil ist ja in der That dasselbe wie das zwischen
dem größern Theil und dem Ganzen.
Fig. 1., Bd. 137, S. 323
Auf geometrischem Wege wird die Eintheilung einer Größe nach diesem Verhältniß
bekanntlich dadurch gefunden, daß man an eine gegebene Linie ab die Hälfte von ab als Kathete bd ansetzt, dann die
Hypotenuse da zieht und hierauf erst de = bd auf der
Hypotenuse und dann ca, d. i. den Rest der
Hypotenuse, als ac auf der ursprünglich gegebenen
Linie ab abträgt: denn in diesem Fall ist ac der gesuchte Major, cb dagegen der gesuchte Minor der ganzen Linie ab, und es verhält sich mithin bc : ac = ac : ab. (Fig. 1.)
Auf arithmetischem Wege findet man dem entsprechend das Maaß des Majors (M) aus dem des Ganzen (T)
nach der Formel: M = √ (T² + T²/4) – T/2. Wird also z.B. T = 10
angenommen, so ist M = √ (10² +
10²/4) – 10/2 = √ (100 + 25) – 5 =
6,₁₈₀₃... Das Maaß des Minors (m) aber ist hienach = T – M, z.B. = 10 –
6,₁₈₀₃... = 3,₈₁₉₇...
Hieraus ist zugleich ersichtlich, daß beide Theile trotz ihrer Bestimmtheit stets
einen irrationalen, unendlichen Bruch des Ganzen bilden, daß sie sich mithin in
Zahlen nie ganz genau ausdrücken lassen, und daß folglich bei jedem Zahlenausdruck
derselben entweder der Major um ein Weniges zu klein und der Minor zu groß, oder
umgekehrt der Major zu groß und der Minor zu klein ausfällt.Gebe ich z.B. von 10 den Major als 6,₁₈ und den Minor als
3,₈₂ an, so ist ersterer um etwa 3/10000 zu klein und
letzterer um eben soviel zu groß. Bestimme ich dagegen den Major als
6,₁₉ und den Minor als 3,₈₁, so ist umgekehrt
jener um etwa 97/10000 zu groß und dieser um eben soviel zu klein angegeben.
So ist, wenn ich die Proportionaltheile von 8 als 3 + 5, und von 13 als 5 +
8 angebe, in jenem Falle der Major, und in diesem Falle der Minor ein wenig
zu groß genommen. Das Verhältniß ist also insofern wirklich ein ideales, in endlichen Größen
nie ganz zu erreichendes; eine wenn auch noch so geringe Abweichung nach der einen
oder der andern Seite hin ist also in der realen Welt geradezu unvermeidlich und die
mehr oder minder vollkommene Realisation dieses Verhältnisses kann daher stets nur
in einer mehr oder minder vollkommenen Annäherung an dasselbe bestehen. Die
praktische Brauchbarkeit desselben wird hiedurch natürlich nicht im Mindesten
geschwächt, im Gegentheil es entspringt daraus für Natur und Kunst der Vortheil, es
nach zwei verschiedenen Seiten hin und in verschiedenen Graden der Vollkommenheit
ausbilden zu können, und späterhin wird sich zeigen, daß hierauf gerade die
wesentlichsten Unterschiede in den Verhältnissen der Erscheinungen, z.B. die
Geschlechtsunterschiede der männlichen und weiblichen Gestalt beruhen.
Dieses Verhältniß (3,₈₁...: 6,₁₈... =
6,₁₈...: 10,₀₀, oder wenn das Ganze als Eins angenommen wird, 0,₃₈₁...:
0,₆₁₈... = 0,₆₁₈...:
1,₀₀₀ = 1,₀₀₀:
1,₆₁₈... etc.) ist nun in der That dasjenige, nach welchem in
consequenter Durchführung die ganze menschliche Gestalt gebaut und gegliedert ist;
noch wichtiger und interessanter aber wird es dadurch, daß auch noch eine große
Anzahl von anderen Erscheinungen, welche durch wohlgefällige Größenverhältnisse
einen ästhetischen Eindruck machen, nach demselben Verhältnisse geformt ist oder sich wenigstens
mehr oder minder genau um dasselbe bewegt, so z.B. die Abstände der Planeten, die
Gestalt vieler Krystalle, der Bau vieler Pflanzen und Pflanzentheile, insbesondere
die von O. Braun entdeckte Blattstellung, die Gliederung
der edlern Thiere, die befriedigendsten und wohlklingendsten der musikalischen
Accorde u.s.w. Ueber alles dieses habe ich mich in einem besonderen WerkeNeue Lehre von den Proportionen des menschlichen
Körpers, aus einem bisher unerkannt gebliebenen, die ganze Natur
und Kunst durchdringenden morphologischen Grundgesetze entwickelt und mit
einer vollständigen historischen Uebersicht der bisherigen Systeme begleitet
von Prof. Dr. Zeising. Mit 177 in den TextTert gedruckten Holzschnitten. Leipzig, R. Weigel. 1854. ausführlich verbreitet und die darin niedergelegte Entdeckung durch Zahlen
und Zeichnungen belegt. Der vorliegende Aufsatz hat daher nur den Zweck,
insbesondere den praktischen Künstler und Techniker auf diese Schrift und das darin
behandelte Proportionalgesetz aufmerksam zu machen, und ich will daher hier nur
diejenigen Punkte berühren, die besonders für ihn von Interesse sind.
Zunächst und hauptsächlich ist natürlich das Gesetz für den Bildhauer und Maler,
sowie für alle an diese sich anreihenden Techniker, z.B. für den Steinmetzen,
Holzschnitzer, den Arbeiter in Metall, Porzellan, Glas, Steinpappe etc., kurz den
Bildner und Zeichner jedweder Art, sofern er es mit der Bildung menschlicher Figuren
zu thun hat, von Wichtigkeit, und zwar nicht bloß in theoretischer, sondern auch in
rein-praktischer Beziehung, weil nach keinem andern System die Zeichnung
einer correcten menschlichen Gestalt so einfach und leicht ist, als nach dem hier in
Rede stehenden.
Theilt man nämlich die Totalhöhe einer menschlichen Figur vom Scheitel bis zur Sohle
genau auf die oben beschriebene Weise nach dem Verh. des goldnen Schnitts, so fällt
der Durchschnitt, wenn dem Minor die obere Lage gegeben wird, stets mit den zwischen
der untersten Rippe und dem Hüftkamm liegenden Weichen oder der Taille, und zwar am
genauesten mit der Basis derselben oder der ein wenig über dem Nabel hinlaufenden
Bauchfalte, welche besonders deutlich beim Bücken hervortritt, also mit der Gränze
zwischen Oberkörper und Unterkörper zusammen. Der Oberkörper ist also der Minor und
der Unterkörper der Major der Totalhöhe und beide bilden mit dem Ganzen, wenn dieses
als Eins angenommen wird, folgende stetige, dem goldnen
Schnitt entsprechende Proportion:
Oberkörper
:
Unterkörper
=
Unterkörper :
Totalhöhe
0,₃₈₁...
:
0,₆₁₈...
=
0,₆₁₈...
1,₀₀₀.
Theilt man die Totalhöhe so, daß der Minor unterhalb des Major zu liegen kommt, so
reicht der Major gerade bis zum Handende des senkreckt herabhängenden Arms. Auch in
diesem Fall correspondirt also der goldne Schnitt mit einem wesentlichen Abschnitt
des Körpers.
Zu nicht minder wesentlichen Körperabtheilungen gelangt man, wenn man die zuerst
angegebene Eintheilung nach demselben Princip weiter verfolgt. Theilt man nämlich
den Oberkörper (vom Scheitel bis zur Taillenbasis), so bezeichnet der Durchschnitt
gerade die Gränze oder schmalste Stelle zwischen der Kopf- und Rumpfpartie in
der Höhe des Kehlkopfs; theilt man hingegen den Unterkörper, so wird dadurch die
Gränze oder schmalste Stelle zwischen Ober- und Unterschenkel am unteren Ende
des Knies oder Anfang der Wade gefunden. Unter- und Oberkörper sind also nach
demselben Verhältniß gegliedert wie der ganze Körper, nur daß ihre Theile in
demselben Verhältniß kleiner sind, in welchem ihre Totalität hinter der Totalhöhe
zurückbleibt. Die beiden Theile des Unterkörpers bilden mithin mit dem ganzen
Unterkörper in Zahlen folgende Proportion:
Unterschenkelpartie
:
Oberschenkelpartie
:
ganzer Unterkörper;
0,₂₃₆...
:
0,₃₈₁...
:
0,₆₁₈...
dagegen die beiden Theile des Oberkörpers mit dem ganzen
Oberkörper folgende:
Kopfpartie
:
Rumpfpartie
:
ganzer Oberkörper
0,₁₄₅...
:
0,₂₃₆...
:
0,₃₈₁...Hat man einmal die Zahlenwerthe der beiden Hauptabcheilungen des
Ganzen gefunden, so gelangt man zu denen der Unterabtheilungen ganz
einfach auf dem Wege der Subtraction des Major vom Ganzen und des
Minor vom Major. Der Major des Majors ist daher =
1,₀₀₀ – 0,₆₁₈... =
0,₆₁₈..., mithin dem Minor des Ganzen gleich,
der Minor des Majors (mM), sowie
auch der Major des Minors (Mm) =
0,₆₁₈... – 0,₃₈₁...
= 0,₂₃₆...; der Minor des Minors (mm), sowie auch der Major vom
Major des Minors (MMm) und der
Major vom Minor des Majors MmM) =
0,₃₈₁... – 0,₂₃₆...
= 0,₁₄₅... u.s.w. Mithin sind die Zahlenwerthe
für alle aus einer fortgesetzten Untereintheilung sich ergebenden
Abschnitte, wenn das Ganze als 1 oder 1000 Tausendstel angenommen
wird, in folgender absteigender Zahlenreihe enthalten:1000 : 618 : 381 : 236 : 145 : 90 : 55 : 34 : 21
: 13 : 8 : 5 : 3.Alle zwischen diesen Zahlen bestehenden Verhältnisse sind bis auf
kleine, der Kürze halber hier unberücksichtigt gebliebene
Bruchtheile einander gleich, z.B. 1000 : 618 = 618 : 381 u.s.w. Als
die einfachsten Typen dieses Verhältnisses in runden Zahlen lassen
sich die Verhältnisse 8 : 5 und 5 : 3 ansehen, und zwar jenes als
Typus derjenigen in denen der Minor, dieses aber als Typus
derjenigen in welchen der Major ein wenig zu groß ist. In noch
kleineren Zahlen läßt sich das Verhältniß ohne Bruch nicht mit
genügender Genauigkeit bezeichnen; doch drückt sich in den
Verhältnissen 3 : 2, 2 : 1 und 1 : 1, welche in runden Zahlen durch
fortgesetzte Subtraction des Minor vom Major gewonnen werden, ein
Uebergang mit oscillirender Bewegung vom Verh. des goldnen Schnitts
zum Verhältniß des Gleichmaaßes (1 : 1) aus.
Nicht anders ist das Resultat, wenn man mit jeder dieser vier Abtheilungen abermals
eine Untereintheilung vornimmt: denn je nachdem man hiebei dem Minor oder Major die
obere Lage gibt, correspondirt der Durchschnitt mit folgenden wesentlichen
Punkten:
1) in der Kopfpartie mit dem Orbitalrande oder der Nasenbasis;
2) in der Rumpfpartie mit der Höhe der Achselhöhlen oder der Herzgrube;
3) in der Oberschenkelpartie mit dem
Schamende oder dem Handende;
4) in der Unterschenkelpartie mit dem
Ende des Wadenmuskels oder der Schienbeintaille, d. i. der schmalsten Stelle
zwischen Wade und Knöchel.
Je nachdem die hieraus resultirenden Abtheilungen mehr oder minder gegliedert sind,
läßt sich mehr oder minder oft dasselbe Eintheilungsprincip auch bei ihnen
verfolgen, am evidentesten in den Abschnitten der Kopf- und Rumpfpartie,
minder scharf markirt, doch immer noch unverkennbar in den Unterabtheilungen der
Ober- und Unterschenkelpartie. Dieß hier ausführlich ins Einzelne zu
verfolgen, erlauben die Gränzen dieses Aufsatzes nicht; ich begnüge mich daher, die
Ergebnisse einer consequent fortgesetzten Subdivision der vier Hauptabschnitte der
Totalhöhe hier nur in einer Uebersicht anzudeuten und die den Abtheilungen
entsprechenden proportionalen Zahlenwerthe beizufügen.
1. Gliederung der Kopfpartie mit dem
Totalmaaß von 145 Tausendsteln der Totalhöhe:
Scheitel bis HaaranfangHaaranfang bis
Augenbrauen
2134
55
Augenbrauen bis NasenbasisNasenbasis
bis KinnKinn bis Kehlkopf
55
343421
90
2. Gliederung der Rumpfpartie mit
dem Totalmaaß von 236 Tausendsteln:
Kehlkopf bis
BrustbeinanfangBrustbeinanfang bis Achselhöhlenhöhe
3455
90
Achselhöhlenhöhe bis
HerzgrubeHerzgrube bis RippenendeRippenende bis
Taillenbasis
90
555534
145
3. Gliederung der Oberschenkelpartie
mit dem Totalmaaß von 381 Tausendsteln:
Taillenbasis bis SchambergSchamberg
bis Schamende
9055
145
Schamende bis HandendeHandende bis
KnieanfangKnieanfang bis Wadenanfang
145
905590
236
4. Gliederung der Unterschenkelpartie mit dem Totalmaaß von 236 Tausendsteln:
Wadenanfang bis zur größten Breite der
WadenGrößte Breite der Waden bis Ende des Wadenmuskels
5534
90
Ende des Wadenmuskels bis
SchienbeintailleSchienbeintaille bis FußanfangFußanfang bis
Fußsohle
90
553455
145
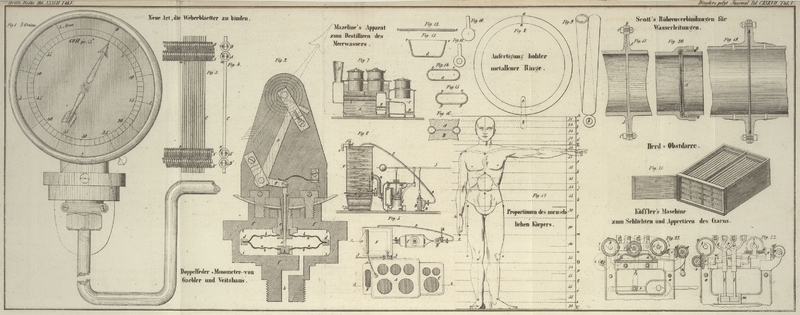
Zur Veranschaulichung dieser Uebersicht dient Fig. 17 auf Tab. V,
welche eine genaue Nachbildung der von Carus in seiner
„Symbolik der menschlichen Gestalt“ zur Darstellung der von
ihm als ideal-normal erkannten Maaßverhältnisse gegebenen Figur ist. Die
Linien und Punkte innerhalb der Figur beziehen sich auf das Carus'sche System; das links von der Figur befindliche Schema nebst den
davon auslaufenden Linien stellt die consequent fortgesetzte Eintheilung der
Totalhöhe dieser Figur nach dem Verhältniß des goldnen Schnitts dar.
Ganz nach dem nämlichen Verhältniß gliedern sich nun auch die Arme, Hände, Füße,
Augen etc., wofür hier die Andeutung genügen möge, daß
der ganze Arm mit Hand als Ganzes
3mal
145... = 437...
der Unterarm mit Hand als Major des
Ganzen
3mal
90... = 270...
der Oberarm als Minor des Ganzen
3mal
55... = 167...
die Hand als Minor des Majors
3mal
34... = 103...
die Vorderhand als Major der
Handlänge
3mal
21... = 63...
Tausendstel der ganzen Körperlänge enthält.
Und so entsprechen auch die Breitedimensionen
wohlgebildeter mittlerer Constitutionen in den wesentlichsten Höhepunkten der
einzelnen Partien und Gliedmassen denselben Verhältnißzahlen. So ist z.B. die größte
Breite des Kopfes = 2mal 55; die Breite des Halses = 2mal 34; die größte Breite des
Rumpfes ohne Arme = 2mal 90; die größte Breite des Rumpfes mit Armen = 2mal 145; die
Breite der Hüften = 2mal 90; die mittlere Breite des einzelnen Schenkels = 90; die
Breite des Knies = 55;
die größte Breite der Wade = 145/2 geringste Breite des Schienbeins = 34, und die
horizontale Ausdehnung des Fußes in der Länge = 145, dagegen in der Breite = 55. Das
Nähere hierüber findet sich in meiner Proportionslehre S. 220–263.
Fig. 2.; Bd. 137, S. 329
Alle für den Bildner und Zeichner richtigen Abschnitte des menschlichen Körpers
lassen sich mithin in ihrem Maaß mit größter Leichtigkeit nach den wenigen und
leicht zu behaltenden Zahlen der aus der fortgesetzten proportionalen Eintheilung
der Zahl 1000 hervorgehenden Reihe: 1000, 618, 385, 236 u.s.w. bestimmen; und eben
so leicht ist natürlich auch die Bestimmung der Maaße auf rein-geometrischem
Wege, besonders wenn man sich ein für allemal einen General-Proportionsmesser
nach Andeutung der beistehenden Figur entwirft und die in meiner Proportionslehre
(S. 451–456) dazu gegebene Gebrauchsanweisung dabei berücksichtigt. (Fig. 2.)
Will z.B. ein Zeichner eine menschliche Figur gerade von der Höhe dieses Maaßstabes,
also = αx entwerfen, so hat er im Major
desselben βx das Maaß für den Unterkörper,
und mithin im Minor αβ = γx (381) das Maaß für den Oberkörper und
zugleich für die Oberschenkelpartie, sowie für die Abschnitte vom Kehlkopf bis zum
Schamende und vom Handende bis zur Sohle: denn alle diese Abschnitte haben das Maaß
von 381. – Im Minor des Majors βγ = δx (236)
besitzt er das Maaß für die Rumpf- und Unterschenkelpartie, sowie für die
Abschnitte vom Scheitel bis zu den Achselhöhlen, von der Taillenbasis bis zum
Handende, vom Schamende bis zum Wadenanfang u.a. – Im nächst kleineren Theil γδ = εx (145) hat er das Maaß für die Kopfpartie, für die Abschnitte vom
Kehlkopf bis zur Herzgrube, von den Achselhöhlen bis zur Taillenbasis, von dieser
bis zum Schamende, vom Handende bis zum Knieende etc., sowie auch für die mittlere
Fußlänge, für die halbe Breite des Rumpfes nebst Armen (in der Höhe der
Achselhöhlen), für die Breite beider Waden etc.; und so liefern ihm auch die
folgenden Abschnitte δε = ζx (90), εζ = ηx (55), ζη = ϑx (34), ηϑ = ιx (21) und ϑι (13) die Maaße für alle ihm wichtigen Abtheilungen, wie
sie auf S. 264 und 265 meiner Proportionslehre tabellarisch zusammengestellt
sind.
Soll die Figur kürzer als die ganze Länge des Maaßstabes, z.B. nur Fx seyn, so muß natürlich für βx der Abschnitt fx, für αβ oder γx der
unter γ beginnende Abschnitt fx, für βγ oder δx der unter δ beginnende Abschnitt fx u.s.w. substituirt werden, weil sich diese nach
der Construction des Maaßstabes zu Fx eben so
verhalten, wie βx, γx, δx etc. zu αx.
Soll hingegen die Figur länger seyn als der Maaßstab αx, so muß man sich denselben nach Bedürfniß verlängern, nämlich
oben an ihn ein auf gleiche Weise eingetheiltes Stück in der Länge von βx, welches α'x heißen möge, dann wieder ein Stück = αx mit der Bezeichnung α''x, hierauf wieder ein Stück = α'x mit der Benennung α''x u.s.w. ansetzen, bis er eine Länge besitzt, wie man sie
gebraucht. Uebrigens verfährt man dann ganz in der bisher beschriebenen Weise.
Natürlich entspricht eine auf solche Weise construirte Figur nur dem Bedürfniß der
Correctheit und entbehrt als solche noch jedes charakteristischen und lebendigen
Ausdrucks; wer aber weiß, daß die Correctheit stets die Basis auch der freieren
Gestaltung seyn und bleiben muß, wird darum die Wichtigkeit eines so leicht zur
Correctheit führenden Verfahrens nicht verkennen, und zwar um so weniger, als dieses
Verfahren, weil es dem Auge und der Hand nur die genaue Erfassung eines einzigen
Verhältnisses zumuthet, weit mehr als alle bisherigen Methoden dazu geeignet ist,
jene Sicherheit und Virtuosität zu erzeugen, welche eines leitenden Kanons nicht
mehr bedarf.
Noch mehr aber empfiehlt sich der hier erörterte Kanon dadurch, daß sich aus ihm
zugleich die allgemeinsten Normen für die Darstellung der wichtigsten Modificationen
der Menschengestalt, namentlich der Geschlechts-, Racen- und
Altersunterschiede ergeben. Wie oben bereits angedeutet ist, läßt sich unser
Verhältniß in endlichen Zahlen und Maaßen nie vollkommen genau realisiren, sondern
der reale Ausdruck weicht immer um einen wenn auch noch so geringfügigen Bruchtheil
von demselben ab, und zwar entweder zu Gunsten des Minors, wodurch sich das
Verhältniß dem Verhältniß der Gleichheit (1 : 1) nähert, oder zu Gunsten des Majors,
wodurch es dem Verhältniß einer noch größeren Verschiedenheit, namentlich dem
Verhältniß der Duplicität (1 : 2) näher kommt. Vergleicht man nun die Verhältnisse
der obigen Zahlenreihe mit einander, so findet man daß die Verhältnisse 5 : 8, 13 :
21, 34 : 55, 90 : 145 u.s.w. den Minor, dagegen die dazwischenliegenden Verhältnisse
3 : 5, 8 : 13, 21 : 34, 55 : 90, 145 : 236 etc. den Major bevorzugen, daß also in
dieser Reihe abwechselnd ein Schwanken nach der einen oder der andern Seite hin
stattfindet. Auf diesem unmittelbar aus der Idealität oder Unendlichkeit des
Verhältnisses sich ergebenden Unterschiede beruht nun merkwürdiger Weise auch die
Hauptdifferenz des menschlichen Körperbaues, nämlich die zwischen dem männlichen und
weiblichen Typus. Der männliche Typus folgt nämlich mit entschiedener Vorliebe den
den Minor bevorzugenden Verhältnissen, unter denen sich das Verhältniß 5 : 8 als das
einfachste und Grundverhältniß darstellt; der weibliche Typus hingegen ist häufiger
nach den den Major bevorzugenden Verhältnissen gebildet, unter welchen das
Verhältniß 3 : 5 als das einfachste und zumeist ausgeprägte anzusehen ist. Beim
männlichen Körper nämlich liegt die Taille in der Regel etwas tiefer als der goldne
Schnitt, beim weiblichen hingegen ein wenig höher; in jenem ist also der Minor, in
diesem der Major ein wenig bevorzugt, was sich außerdem auch darin ausdrückt, daß
bei den Männern Kopf und Brust als Theile des Oberkörpers, bei den Frauen dagegen
Hüften und Waden als Theile des Unterkörpers völliger gebaut sind, wie sich denn
überhaupt nach Seite 298 fgg. meiner Proportionslehre alle formellen
Geschlechtsunterschiede als einfache Konsequenzen dieses Grundunterschiedes
darstellen.
Auf ähnlichen Schwankungen beruhen nun auch die Racen- und Altersunterschiede,
nur daß hier die Abweichungen von der idealen Mitte des Verhältnisses nach beiden
Seiten hin noch stärker sind, dergestalt daß sie sich in den minder entwickelten
Formen um das Verhältniß der Gleichheit (1 : 1) dagegen in den übermäßig
entwickelten Formen, wie sie in Uebergangsperioden vorzuherrschen Pflegen, um das
Verhältniß der Duplicität (1 : 2) bewegen, über diese Extreme aber nur sehr selten
hinausgehen. Auch die Darstellung des Eigenthümlichen und Charakteristischen in der
Menschengestalt findet also in dem hier besprochenen Proportionalgesetz einen
sicheren Anhalt, worüber man außer meiner Proportionslehre (S. 309 fgg.) auch meine
„Aesthetischen Forschungen“ (§ 186, 196 fgg.)
vergleichen möge.
Nächst dem Bildner und Zeichner menschlicher Figuren ist nun dieses Gesetz
selbstverständlich auch für alle diejenigen von wesentlicher Bedeutung, die es mit der Bekleidung,
Costümirung und Ausschmückung des menschlichen Körpers zu thun haben, also für den
Schneider, Modisten, Schnürleibfabrikanten, Waffenschmied u.s.w.: denn es liegt auf
der Hand, daß nur die Ausstattung wirklich als schön
gelten kann, die mit den normalen und charakteristischen Verhältnissen des Körpers
selbst im Einklang ist. Dieß ist vom Gefühl auch stets empfunden, und daher ist man
von jeher bestrebt gewesen, in und an der Bekleidung die drei Hauptcäsuren des
Körpers gehörig hervorzuheben, nämlich die Taille durch den Gürtel, den Hals durch
das Halsband und den Wadenanfang als Gränze zwischen Ober- und Unterschenkel
durch den Kniegürtel oder durch das Ende des Rockes. Nicht selten gerathen aber
Geschmack und Mode bei Bestimmung dieser und anderer für die Gliederung der Gestalt
wichtigen Punkte auch auf Irrwege, und ein leitender Kanon ist daher hier nichts
weniger als überflüssig. Nähere Andeutungen hierüber habe ich bereits im Morgenblatt (1854, Nr. 17 und 18) gegeben, und will ich
daher hier der Kürze halber darauf verweisen.
Von nicht geringerer Wichtigkeit ist nun aber ein zuverlässiges Proportionalgesetz
auch für eine große Anzahl anderer Künstler und Techniker, die es nicht unmittelbar
mit dem menschlichen Körper zu thun haben, namentlich für den Architekten, sodann
aber auch für Tischler, Gold und Silberarbeiter, Glas- und
Porzellanfabrikanten, Formschneider, kurz für Alle, die es mit der Anfertigung von
Gefäßen, Tafelaufsätzen, Lampen, Leuchtern, Kandelabern, Uhren, Teppichen, Tapeten,
Stickmustern und sonstigen Gebrauchs- und Luxusartikeln zu thun haben; ja man
kann sagen, es thut hier in noch höherem Grade noth, einerseits weil hier die
natürlichen Vorbilder fehlen und mithin der subjectiven Willkür mehr Thür und Thor
geöffnet ist, andererseits weil viele der Arbeiter, die solche Artikel zu fertigen
haben, nicht in gleichem Maaße wie der Maler, Bildhauer und der eigentliche
Architekt eine durchgreifende Geschmacksbildung erhalten haben. Wie sehr nun das
Verhältniß des goldnen Schnitts auch in dieser Hinsicht sich als dasjenige
empfiehlt, um welches herum man sich bei Bestimmung der Formen zu bewegen hat, und
von welchem man, wenn man nicht das ästhetische Gefühl verletzen will, nicht
allzuweit abweichen darf, geht deutlich daraus hervor, daß man in einer großen
Anzahl von architektonischen und verwandten Kunstwerken und zwar gerade solchen, die
unbestritten als die schönsten anerkannt sind, unbewußt und unwillkürlich, also rein
in Folge des natürlichen Schönheitsgefühls, davon Anwendung gemacht hat.
In Betreff der Architektur habe ich hierüber in meiner
Proportionslehre (S. 390–410) eine Reihe überzeugender Belege gegeben, von
denen ich hier nur
auf einige hindeuten will. So verhält sich z.B. am Parthenon zu Athen die Höhe
desselben (von der Grundlinie der Basis bis zur Spitze des Giebels) zur Länge des
Architravs genau wie der Minor zum Major: denn nach den arithmetischen Maaßangaben
besteht die Höhe dieses vollendetsten aller antiken Bauwerke aus 65, dagegen die
Breite, d. i. die Länge der Giebelfront, aus 107, mithin die Summe beider
Dimensionen aus 172 Fuß. Theilt man aber diese Zahl nach dem goldnen Schnitt, so
kommen auf den Major 106–107, auf den Minor 66–65 Fuß; beide Theile
entsprechen also bis auf einen für die Wahrnehmung völlig verschwindenden Bruchtheil
den oben angegebenen Maaßen. In gleich überraschender Weise stimmt die Eintheilung
der Höhe mit unserem Gesetz überein. Theilt man diese nämlich nach dem goldnen
Schnitt, so reicht der längere Untertheil gerade bis zur Grundlinie des Gebälks und
der kürzere Obertheil von da bis zur Spitze des Giebels; der Major correspondirt
also mit der Höhe der Säulen nebst den Stufen, der Minor hingegen mit der Höhe des
Gebälks nebst der Höhe des Giebels. Unterwirft man den Obertheil wieder derselben
Theilung, so fällt die Durchschnittslinie gerade mit der Grundlinie des Giebels,
also der Gränze zwischen Giebel und Gebälk, zusammen; nimmt man aber auch mit dem
Gebälk die Theilung vor, so entspricht die Höhe des Architravs dem Minor und die
Höhe des Frieses und der Corniche zusammengenommen dem Major; im letztem Abschnitt
aber stehen der Fries als Major und die Corniche als Minor zu einander wiederum in
dem nämlichen Verhältnisse. Interessant ferner ist, daß sich auch die Höhe des
nackten Säulenschafts zur summirten Höhe der Basis einerseits und des Capitäls sammt
dem Gebälk andererseits wie der Major zum Minor verhält, und daß alsdann zwischen
der Höhe der Basis und der Höhe des Capitäls sammt Gebälk, also zwischen dem
unterhalb und dem oberhalb des Schaftes liegenden Bau (mit Ausschluß des Giebels)
abermals dasselbe Verhältniß besteht.
In nur wenig abweichender Weise finden sich dieselben Proportionen auch an andern
antiken Bauwerken von hervorragender Schönheit wieder z.B. an den Propyläen der
Akropolis, am Erechtheum, am Theseustempel, am Jupitertempel zu Agrigent, am
Apollotempel zu Bassä, am Tempel des capitolinischen Jupiter zu Rom, am Denkmal des
Lysikrates, sowie an vielen Triumphbogen, Mausoleen, Wasserleitungen etc.; von
besonderem Interesse aber ist es, daß sich die verschiedenen Verhältnisse der
Säulenordnung, durch die sich u.a. der dorische und ionische Styl von einander
unterscheiden, zur reinen Mitte unseres Verhältnisses gerade eben so verhalten, wie
die oben erwähnten Modificationen, auf denen die Unterschiede des männlichen und
weiblichen Typus beruhen: denn in der Bestimmung des Verhältnisses der
Säulendicke zum Säulenabstand zeigt der dorische Styl, wie der männliche Typus eine
entschiedene Vorliebe zur Bevorzugung des Minors, also eine Hinneigung zum
Verhältniß 1 : 1, ungefähr bis zum Verhältniß 2 : 3; der ionische Styl hingegen, wie
der weibliche Körperbau, zeigt eine Inclination zur Bevorzugung des Majors, also zum
Verhältniß 1 : 2, ja 1 : 3, ein Umstand, aus dem sich mit Evidenz der männliche
Charakter des dorischen und der weibliche Charakter des ionischen Styls erklärt, und
welcher dadurch eine noch allgemeinere Wichtigkeit erhält, daß auf derselben
Differenz auch der Unterschied zwischen Dur- und
Moll-Schlußaccord in zweistimmigen
Musikstücken beruht: denn der zweistimmige Dur-Schlußaccord, d. i. die kleine Sexte
(z.B. e + ) beruht auf dem Schwingungsverhältniß
5 : 8, in welchem der Minor bevorzugt ist, und der
zweistimmige Moll-Schlußaccord, d. i. die große Sexte (z.B. es +
) beruht auf dem Schwingungsverhältniß 3 : 5, in welchem der Major ein wenig zu groß ist.
Wie an antiken Bauwerken findet sich nun das Verhältniß des goldnen Schnitts oft mit
überraschender Consequenz auch an Werken der gothischen Baukunst beobachtet,
namentlich was die Eintheilung der Höhe betrifft. In meiner Schrift habe ich dieß
insbesondere am Kölner Dom, am Freiburger Münster und an der Elisabethkirche zu
Marburg nachgewiesen und durch Zeichnungen veranschaulicht; außerdem aber können
noch eine große Anzahl anderer berühmter Gebäude, z.B. Notre Dame zu Paris, die
Kathedralen zu Amiens, Lincoln, York, Canterbury, Salisbury, Liechfield, Palermo,
Siena etc., sowie viele deutsche Kirchen und Dome gleich überzeugende Belege dafür
liefern. Auch für anderweitige öffentliche und Privatgebäude empfiehlt sich die
Anwendung des Verhältnisses, z.B. zur Bestimmung bei Maaßverhältnissen zwischen der
Höhe des Souterrains und des Erdgeschosses, der Hauptetage und der darüberliegenden,
des obersten Geschosses und des Dachgesimses, der Fensterbrüstung und des Fensters
etc., sowie auch zwischen der Breite des Hauptflügels und der Seitenflügel, der
Fenster und der Fensterwände, der Thürflügel und der Thürbekleidung u.s.w.
Nicht minder anwendbar als für die Construction und Gliederung ganzer Gebäude ist das
Gesetz auch für die Gestaltung einzelner Bestandtheile derselben, z.B. der Thüren,
FensterBei Eintheilung der Fensterhöhe durch den Querbalken des Fensterkreuzes hat
man bisher zwischen den Verhältnissen 1 : 1 und 1 : 2 geschwankt, indem man
entweder jeder der beiden Abtheilungen 2, oder der untern 2, dagegen der
obern nur 1 Scheibe gab. Ein unschönes Hinausgehen über das letztere
Verhältniß findet dann statt, wenn sich die Zahl der Scheiben in beiden Abtheilungen
wie 1 : 3 verhält; dagegen eine Vermittlung jener beiden zuerst genannten
Verhältnisse wird erstrebt, wenn man, wie im Schinkel'schen Fenster, der oberen Abtheilung 2, und der unteren 3
Scheiben gibt, oder wenn man, was neuerdings beliebt ist zwar jede
Abtheilung nur aus einer Scheibe bestehen läßt,
aber der unteren 3/5 und der oberen 2/5 der ganzen Fensterhöhe gibt. Hierin
ist schon eine entschiedene Annäherung an das Verhältniß des goldnen
Schnitts enthalten; noch wohlgefälliger aber und zugleich praktischer wird
es seyn, die Höhe der oberen Abtheilung zur Höhe der unteren Abtheilung sich
wie 3 : 5 oder wie 5 : 8 verhalten zu lassen, weil man auf diese Weise für
den unteren Flügel noch an Höhe gewinnt, ohne die Höhe der oberen Flügel,
wie bei dem Verhältniß 1 : 2 der Fall ist, bloß auf die Hälfte von der Höhe
der untern Flügel zu reduciren., Treppen, Gesimse, Consolen, Arabesken und sonstigen Ornamente. Die ästhetische
Bedeutung derselben folgt schon daraus, daß die den Formen dieser Gegenstände zum
Grunde liegenden geometrischen Figuren, z.B. Dreiecke, Oblongen, Rhomben, Achtecke,
Ellipsen, Ovale, Kreuze, Sterne u.s.w., gerade dann eine dem Auge wohlthuende
Gestalt haben, wenn sie auf die eine oder die andere Weise nach dem Verhältniß des
goldnen Schnitts gebildet sind, z.B. wenn sich Länge und Breite, Grundlinie und
Höhe, längere und kürzere Seite, längerer und kürzerer Radius oder sonstige im Maaß
verschiedene Dimensionen einer Figur gerade wie Major und Minor oder wie ein Product
derselben zu einander verhalten. So ist z.B. eine Ellipse, in welcher sich die
kürzere Achse zur längeren entweder wie der Major zum Ganzen, also ungefähr wie 5 :
8, oder wie der doppelte Minor zum Ganzen, also etwa wie 6 : 8, verhält, eine sehr
wohlgefällige; und ein dem Schönheitssinn entsprechendes Oval – nämlich das
der Kopfform zum Grunde liegende – läßt sich vielleicht auf keine andere
Weise so leicht und sicher als mit Hülfe des goldnen Schnitts construiren, indem es
ganz einfach durch die Verbindung zweier in zwei Punkten sich schneidenden Kreise
herzustellen ist, von denen der größere einen Halbmesser vom Maaße des Majors, der
kleinere dagegen, dessen Centrum in der Peripherie des größern liegen muß, einen
Halbmesser vom Maaße des Minors hat. Selbst die Wellenlinie, deren ästhetische
Wichtigkeit stets erkannt, in ihren Maaßverhältnissen aber ohne nähere Bestimmung
geblieben ist, läßt sich, wie ich in meinen „Aesthetischen
Forschungen“ (§ 179) gezeigt habe, in den zumeist
befriedigenden Formen bequem nach unserem Verhältniß construiren.Die auf diese Weise entstehenden Wellenlinien sind dieselben, auf denen die
Conturen der menschlichen Gestalt beruhen; auch die besonders wohlgefälligen
Schwingungen der Gebirgskämme pflegen ihnen zu entsprechen. Und so stehen auch gewisse eigenthümliche Verhältnisse der Spirallinie, aus
denen die Gebrüder Bravais die Gesetze der Blattstellung
abgeleitet haben, mit unserem Gesetze und einer ihm entsprechenden Kreiseintheilung,
wie meine Proportionslehre (S. 372) nachweist, in nothwendigem und engstem
Zusammenhange.
Hieraus ergibt sich zugleich seine Bedeutung für die Formation von Vasen, Bechern,
Urnen, Schalen, Leuchtern und ähnlichen Gegenständen: denn sofern diese nicht
Nachbildungen organischer Gebilde sind, stellen sie sich stets, als mehr oder minder
zusammengesetzte Combinationen geometrischer Formen dar. Von besonderer Wichtigkeit
ist hier das Gesetz, wie die Proportionalität überhaupt, für die Eintheilung der
Höhe z.B. bei einem Becher die Bestimmung der Gränze zwischen dem tragenden und dem
getragenen Theil, und an jedem dieser beiden Haupttheile die Maaßbestimmungen für
die Absätze, Schichten, Einziehungen und Ausbauschungen, für die zur Inschrift oder
zu bildlichen Darstellungen bestimmte Abtheilung, für die Randverzierungen u.s.w. In
sehr vielen Fällen läßt sich aber auch das Verh. der Breite zur Länge, resp. Höhe
entweder für das Ganze oder für einzelne Theile desselben, so wie die Gliederung der
horizontalen Ausdehnung, namentlich die Untereintheilung der beiden zu einander
gewöhnlich gegenständlich-symmetrisch sich verhaltenden seitlichen Hälften,
die Articulation des Umrisses, die concentrische Schichtung des vom Umriß
umschlossenen Raumes etc. auf eine geschmack-befriedigende Weise nach
demselben Verhältniß bestimmen z.B. das Format von Postamenten, Schränken, Commoden,
Tischplatten, Kästchen, Spiegeln, Bilderrahmen, Büchern, Füllungen, Abfachungen
etc., das Maaß des concreten Mittelstücks im Verhältniß zum Maaß der dasselbe
umspielenden Lineamente und Schnörkel bei Rosetten, Arabesken, Agraffen etc.; der
Maaßunterschied breiterer und schmälerer Abtheilungen (z.B. der Triglyphen und
Metopen) bei Friesverzierungen, Brüstungen, Geländern, Einfassungen, Bordüren,
Tapisserien, Draperien u.s.w.
Vielleicht taucht in Manchem hiebei die Befürchtung auf, es müsse eine allgemeinere
und mit Bewußtseyn ausgeführte Anwendung des hier in Rede stehenden Verhältnisses
nothwendig zu einer gewissen Monotonie und Gleichartigkeit der Formen und zu einer
Beschränkung der freischaffenden Phantasie führen. Diese Besorgniß ist aber eine
durchaus unbegründete: denn das Verhältniß ist einer so unendlich mannichfaltigen
und verschiedenartigen Ausbildung im Einzelnen fähig, und es läßt der schöpferischen
Kraft innerhalb seiner Gränzen noch einen so unbegränzten Spielraum, daß in keiner
Hinsicht eine beengende Wirkung von ihm zu befürchten ist. Dieß ergibt schon daraus,
daß eine große Anzahl natürlicher und künstlerischer Gebilde, wie die
Menschengestalt, die Figur der schöneren Thiele, der Bau der Pflanzen, die Form
vieler Krystalle, die Anordnung der Planeten, die Construction antiker,
mittelalterlicher und moderner Bauwerke, die harmonische Verbindung von Tönen, und so noch viele andere
Formationen wirklich auf diesem Verhältniß beruhen, ohne daß dadurch ihre
Verschiedenheit und Mannichfaltigkeit irgend einen Abbruch erlitten hätte, ja ohne
daß das zum Grunde liegende Gesetz dem beobachtenden Sinne und forschenden Geiste
auch nur mit Klarheit zum Bewußtseyn gekommen wäre. Es erklärt sich aber diese
unendliche Variabilität und die damit verbundene Schwererkennbarkeit des
Verhältnisses noch deutlicher daraus, daß es sich bald bei dieser, bald bei jener
Dimension, bald an den inneren Achsen einer Figur, bald an ihren äußeren Umrissen,
bald bei der Eintheilung der Linien, bald bei der Eintheilung der Winkel, bald in
einfacherer, bald in complicirterer Weise anwenden läßt, und daß es in seiner
ursprünglichen Reinheit rein idealer, irrationaler Natur ist und daher bei der
Realisation nothwendig gewisse Modificationen erleiden muß, deren Zahl, weil sie auf
der unbegränzten Feinheit von Gradunterschieden beruht, nach zwei verschiedenen
Seiten hin eine schlechthin unendliche ist. Schon die Eintheilung einer einzigen,
einfachen Linie nach diesem Verhältniß kann, je nachdem die Eintheilung einmal,
zweimal, dreimal oder öfter angewandt wird, und je nachdem der Minor bald oberhalb,
bald unterhalb des Majors, oder auch in die Mitte seiner Unterabtheilungen gelegt
wird, eine unberechenbar verschiedene seyn. Nimmt man z.B. als Totalmaaß der Linie
1000 Tausendstel an, so sind u.a. folgende mehr oder minder complicirte
Eintheilungen und Anordnungen von oben nach unten, oder von rechts nach links, oder
von innen nach außen möglich: bei einmaliger Theilung:
381 + 618, und umgekehrt 618 + 381; bei zweimaliger
Theilung: 381 + 236 + 381, oder 381 + 381 + 236, oder 236 + 381 + 381, oder 618 +
236 + 145, oder 145 + 236 + 618 etc.; bei dreimaliger
Theilung: 145 + 236 + 381 + 236, oder 381 + 236 + 145 + 236, oder 236 + 381 + 145 +
236 etc.; bei viermaliger Theilung: 145 + 236 + 236 + 236
+ 145, oder 236 + 145 + 236 + 145 + 236, oder 145 + 236 + 236 + 145 + 236 u.s.w. in infinitum. – Will man nicht vom Ganzen zu den
Theilen, sondern von den Theilen zu dem Ganzen gelangen, so lassen sich die Theile
auch in aufsteigender, absteigender oder wechselnder Progression an einander reihen,
z.B. 3 + 5 + 8 + 13, oder 13 + 8 + 5 + 3, oder 3 + 5 + 8 + 5 + 3, oder 8 + 5 + 3 + 5
+ 8 etc. Jede dieser möglichen Eintheilungen läßt sich natürlich mit jeder andern
theils an derselben Achse, theils an einer andern Achse, oder auch an den Seiten, an
den Winkeln etc. in Verbindung setzen, und so sind noch zahllose andere
Combinationen möglich, so daß der berechnende Verstand nicht einmal im Stande ist, sie unter allgemeine
Rubriken zu bringen.
Uebrigens versteht sich von selbst, daß, wenn hier das Verh. des goldenen Schnitts
als das vollkommenste bezeichnet und dem Techniker zur Benutzung empfohlen ist,
damit nicht gemeint seyn kann, daß es überall und in allen Beziehungen angewandt
werden müsse. Neben ihm besteht z.B. das für den Bildner nicht minder wichtige
Gesetz des Gleichmaaßes oder der Symmetrie unangetastet fort, und zwar läßt sich das Verhältniß beider zu
einander so bestimmen, daß das Verh. des Gleichmaaßes das ursprünglichste und
einfachste, das des goldenen Schnitts hingegen das vollendetste und in sich
abgeschlossenste ist. Jenes bildet daher die Basis, dieses die Culmination der
formellen Entwickelung, jenes prävalirt, wie das Gleichgewicht, in der horizontalen,
dieses, wie die Combination eines größeren und geringeren Gewichts, in der
verticalen Richtung. Jenes befriedigt, weil in seiner Gesetzmäßigkeit sofort
erkennbar, auf der Stelle, wird aber auf die Dauer monoton und langweilig; dieses
besitzt, weil es seine Gesetzmäßigkeit verhüllt, etwas Mystisches und Räthselhaftes,
wirkt aber gerade dadurch in höherem Grade anregend und geistbeschäftigend.
Außer diesen beiden Hauptverhältnissen gibt es ferner noch eine unendliche Masse
anderer Verhältnisse, theils solche, die zwischen beiden in der Mitte liegen, wie
die Verhältnisse 2 : 3, 3 : 4, 4 : 5, 5 : 6 u.s.w., denn in allen diesen sind die
beiden mit einander verbundenen Theile weder einander vollkommen gleich wie in dem
Verhältniß der Symmetrie (1 : 1), noch in dem Grade von einander verschieden, wie im
Verhältniß des goldenen Schnitts (1 : 1,61...); theils solche, welche über das Verh.
des goldenen Schnitts hinausgehen, wie 1 : 2, 1 : 3, 1 : 4, 2 : 5, 3 : 7 etc. Auch
unter diesen Verhältnissen sind viele von ästhetischer Bedeutung, besonders die
zuerst genannten und diejenigen der letztern, welche sich als bloße Producte oder
Potenzen der beiden Hauptverhältnisse auffassen lassen, wie z.B. 1 : 2, 1 : 3 als
Verdoppelung und Verdreifachung des Verhältnisses 1 : 1; und 3 : 10, 5 : 16 als
Verdoppelungen der Verhältnisse 3 : 5, 5 : 8 etc. Im Allgemeinen qualificiren sich
aber dieselben nicht zur Formbestimmung des Ganzen weder in seiner ursprünglichen,
noch in seiner vollendeten Gestalt, sondern nur zur Gestaltung der untergeordneten
Theile und der vom Anfang zum Schluß überleitenden Momente, so daß sie sich als Theil- oder Uebergangsverhältnisse bezeichnen lassen. Als solche sind sie eben so
wichtig und nothwendig als jene, selbst wenn sie, absolut betrachtet, als
Mißverhältnisse erscheinen sollten. So wirken z.B. in der Musik die Secunden und Septimen mit den
Verhältnissen 8 : 9 und 5 : 9, für sich allein genommen, als Dissonanzen; ja auch
die Verhältnisse der Quinte (2 : 3), Quarte (3 : 4) und der beiden Terzen (4 : 5 und
5 : 6) gewähren nicht eine so selbstständige Befriedigung, daß sich das Ohr zum
Schluß bei ihnen zu beruhigen vermöchte. Aber inmitten einer fortschreitenden Reihe
von Accorden sind sie von ganz außerordentlichem Effect: denn sie lassen gleichsam
die einzelnen Töne als mit einander im Conflict erscheinen, und erzeugen dadurch
diejenige Spannung und Aufregung, welche vorangehen muß, wenn das Beruhigende und
absolut Befriedigende der reinen Harmonie in seiner vollen Schönheit erscheinen
soll. Ebenso ist es nun auch bei den optischen Erscheinungen. Ein Verhältniß der
Breite zur Höhe, wie es z.B. die Figur einer einzelnen Säule darstellt, muß, absolut
betrachtet, schon als ein Mißverhältniß angesehen werden; aber als integrirender
Theil einer Säulenhalle, deren Gesammtform auf einem harmonischen Verhältniß wie 3 :
5 oder 5 : 8 beruht, trägt es wesentlich zur Steigerung und Belebung des Effects
bei, indem es den anschauenden Sinn und Geist zunächst aus seiner Ruhe aufregt, dann
aber ihm Gelegenheit gibt, die einzelnen Theile zu einer harmonischen Totalität
zusammen zu fassen.
Durch die hier ausdrücklich hervorgehobene ästhetische Bedeutung, welche das Verh.
der Symmetrie einerseits und die zuletzt erörterten Verhältnisse andererseits
besitzen, wird jedoch die Suprematie des auf dem goldenen Schnitt beruhenden
Verhältnisses nicht aufgehoben, sondern sie läßt sich gerade aus einer Vergleichung
beider mit ihm um so deutlicher erkennen: denn es leuchtet ein, daß dasselbe die
Vorzüge beider in sich vereinigt, indem es einerseits das Beruhigende vom Verhältniß
der Gleichheit und andererseits das Anregende und Belebende von den übrigen
Verhältnissen besitzt. Indem es nämlich die Ungleichheit und Gebrochenheit der
einzelnen Theile durch eine Gleichheit und Continuität der Verhältnisse zwischen dem
Ganzen und seinen Theilen zur Ausgleichung bringt, läßt es uns inmitten der Ruhe
noch die Bewegung und inmitten des Conflicts schon den Frieden empfinden. Daher
bestimmt sich denn auch der ästhetische Rang der übrigen Verhältnisse nach der
nähern oder fernern Beziehung, die sie zum Verh. des goldenen Schnitts haben, und
dieses ist dasjenige Verhältniß, um welches herum sich alle übrigen Verhältnisse wie
um ihre ideale Mitte bewegen. So liegen z.B. unter den musikalischen Verhältnissen
die der Secunden, Terzen, Quarten und Quinten (8 : 9, 5 : 6, 4 : 5, 3 : 4, 2 : 3)
diesseit desselben, d.h. sie nähern sich ihm mehr und
mehr von dem Verhältniß des Gleichmaaßes oder der Prime (1 : 1) aus; dagegen die
Verhältnisse der verschiedenen Septimen (64 : 125, 8 : 15, 5 : 9, 9 : 16, 125 : 216,
75 : 128) liegen jenseit desselben, d.h. sie nähern sich
ihm vom Verhältniß der Duplicität oder der Octave (1 : 2) oder von Verhältnissen
einer noch größeren Differenz aus.
In ganz ähnlicher Weise zeigt sich dieses Verhältniß auch als das mittlere bei
optischen Erscheinungen, z.B. in der Anordnung des Planetensystemes. Die mittleren
Abstände der Planeten von der Sonne sind in runden Zahlen bekanntlich folgende:
Mercur
8 Mill.
Mars
32 Mill.
Saturn
196 Mill.
Venus
15 „
Asteroiden
55 „
Uranus
395 „
Erde
21 „
Jupiter
108 „
Neptun
626 „
Die Entfernungen des Mercur von der Sonne, der Venus vom Mercur, der Erde von der
Venus etc. drücken sich also in folgenden runden Zahlen aus: 8, 7, 6, 11, 23, 53,
88, 199, 231. Die erste Distanz verhält sich also zur zweiten wie 8 : 7, die zweite
zur dritten wie 7 : 6, die dritte zur vierten wie 6 : 11 u.s.w. Drücken wir diese
Verhältnisse, um sie mit dem Verh. des goldenen Schnitts (1 : 1,₆₁...)
bequem vergleichen zu können, sämmtlich in Decimalbrüchen aus und zwar so, daß die
kleinere Zahl stets als 1, die größere dagegen stets als 1 oder 2 mit einem
Decimalbruch erscheint, so erhalten wir folgende Verhältnisse:
Sonne-Mercur
7
: 8 = 1 : 1,₁₄...
Mercur-Venus
6
: 7 = 1 : 1,₁₆...
Venus-Erde
6 : 11
= 1 : 1,₁₆...
Erde-Mars
11 : 23 = 1 :
2,₀₉...
Mars-Asteroiden
23 : 53 = 1 :
2,₃₀...
Asteroiden-Jupiter
53 : 88 = 1 :
1,₆₆...
Jupiter-Saturn
88 : 199 = 1 :
2,₂₆...
Saturn-Uranus
199 : 231 = 1 : 1,₁₆...
Uranus-Neptun
231 : 374 = 1 : 1,₆₁...
Sämmtliche Verhältnisse schwanken also zwischen den Verhältnissen 1 :
1,₁₄... und 1 : 2,₃₀... Zwischen diesen beiden Extremen
bildet aber das Verh. 1 : 1,₆₁..., also das Verhältniß des goldenen
Schnitts das mittlere Proportionalglied; und wenn man aus allen diesen Verhältnissen
das Durchschnittsverhältniß zieht, erhält man das Verh. 1 : 1,₆₉,
welches dem Verh. des goldenen Schnitts ebenfalls sehr nahe kommt.
Zu einem ähnlichen Resultate gelangt man, wenn man z.B. an Pflanzen die Längenmaaße
der zunächst zusammenliegenden Stängelglieder, oder an Thieren die Maaße der nächst
zusammengehörigen Gliedmaßen mit einander vergleicht, worüber ich mir den Nachweis für
eine besondere Abhandlung vorbehalten muß. Dasselbe läßt sich, wie bereits erwähnt,
auch an architektonischen, plastischen und industriellen Kunstwerken beobachten, und
es dürfte daher wohl kaum noch einen Zweifel erleiden, daß sich die Natur und das
unmittelbare künstlerische Gefühl bei ihren Schöpfungen in formeller Beziehung in
bald strengerer, bald freierer Ausführung um das hier erörterte Verhältniß zu
bewegen pflegen.
A. Zeising.
Tafeln