| Titel: | Neue Construction der Tangential-Turbinen; von H. v. Mengershausen. |
| Fundstelle: | Band 152, Jahrgang 1859, Nr. XXII., S. 85 |
| Download: | XML |
XXII.
Neue Construction der Tangential-Turbinen;
von H. v.
Mengershausen.
Aus der Zeitschrift des österreichischen
Ingenieur-Vereins, 1859 S. 1.
Mit Abbildungen auf Tab.
II.
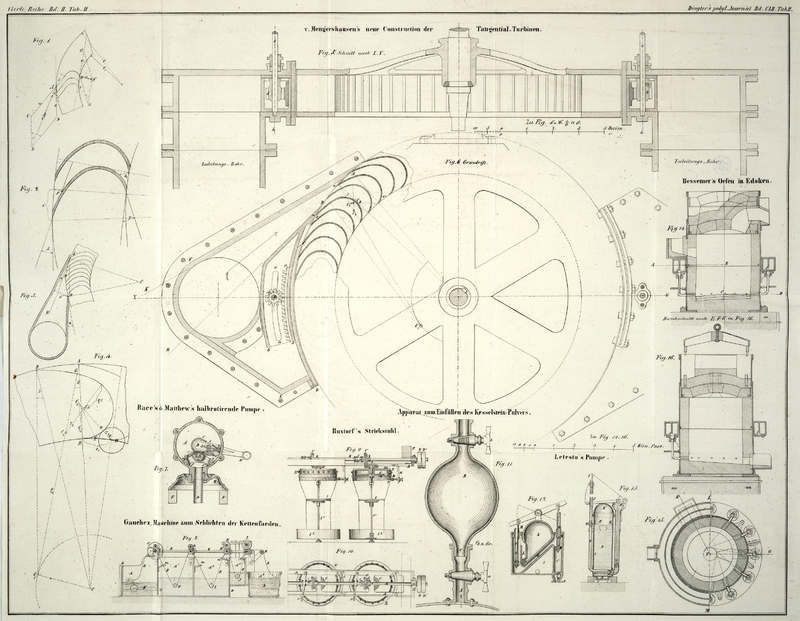
Mengershausen's neue Construction der
Tangential-Turbinen.
Es kann nicht meine Absicht seyn, eine neue Theorie für die
Tangential-Turbinen aufzustellen, indem die Grundzüge derselben bereits
genügend in dem Lehrbuche der Ingenieur- und Maschinenmechanik von Weisbach, in den Vorträgen über Maschinenbau von Redtenbacher und in der Zeitschrift „der
Civil-Ingenieur“ von Bornemann
entwickelt worden sind, sondern ich habe mir die Aufgabe gestellt, eine Construction
der Tangential-Turbinen zu geben, welche nicht nur den Grundsätzen der
Theorie entspricht, sondern auch zur Ausführung einfach genug ist.
Die Vortheile, welche die Tangential-Turbinen in gewissen Fällen vor den
Vollturbinen und Wasserrädern haben, sind so erheblich, daß sie denselben gewiß recht bald eine
ausgebreitete Anwendung verschaffen werden, und daß es daher zeitgemäß ist, die
Construction dieser Räder auch vom praktischen Standpunkte aus zu betrachten.
Das Güteverhältniß der gewöhnlichen Wasserräder nimmt mit dem Gefalle des Wassers zu,
und fällt am Günstigsten beim oberschlächtigen Rade für hohe Gefalle aus, besonders
wenn die Füllung des Rades gering genommen wird.
Der Nutzeffect der Vollturbinen nimmt dagegen mit wachsendem Gefälle ab. Dieselben
sind daher für sehr hohe Gefälle nicht zu empfehlen, ja bei geringer Wassermenge
meistens sogar unausführbar, da sie zu klein ausfallen und eine zu große
Umdrehungszahl ergeben.
Für die Erzielung des größten Nutzeffectes ist es daher angezeigt, bei hohen Gefällen
das oberschlächtige Rad zu wählen; allein in der Praxis tauchen doch oft viele
Gründe auf, welche die Vermeidung des oberschlächtigen Rades selbst mit einiger
Aufopferung an Nutzeffect wünschenswerth machen. Besonders sind es die Bau-
und Reparaturkosten, welche hier in die Waagschale fallen. Dieselben werden, wenn
das Gefälle über 10 bis 12 Meter steigt, oft so groß, daß sie nicht im Verhältniß zu
der ganzen Betriebskraft stehen, indem diese hohen Gefälle doch meistens mit
geringer Wassermenge verbunden sind.
Außerdem fällt man bei diesen großen Wasserrädern bezüglich der Umdrehungszahl im
Vergleich zu den Vollturbinen in das andere Extrem, indem dieselbe so gering wird,
daß man sich für die meisten Zwecke zu ganz bedeutenden Räderübersetzungen
entschließen müßte, welche den Nutzeffect wieder verringern und zur Vertheuerung der
Anlage beitragen.
In einem solchen Falle nun, in welchem also die Vollturbine nicht mehr ausführbar und
zweckmäßig und das oberschlächtige Rad aus den angeführten Gründen unbequem wird,
ist die Tangential-Turbine an ihrem Platze.
Sie bietet uns folgende Vortheile:
1) Durch eine zweckmäßige Wahl des Durchmessers der Turbine hat man es vollständig in
der Hand ihr eine Umdrehungszahl zu geben, welche dem Zwecke angemessen ist, ohne
dadurch am Güteverhältnisse etwas aufzuopfern.
2) Das Güteverhältniß der Tangential-Turbine, oder das Verhältniß des
Nutzeffectes zum absoluten Effect der Wasserkraft, kann selbst bei sehr
veränderlicher Wassermenge stets constant erhalten werden und man hat allen Grund,
dasselbe nicht unter 60 Proc. anzunehmen.
3) Ist als ein weiterer Vortheil der Tangential-Turbine anzuführen, daß ihre
Construction einfach und daher ihre Anfertigung leicht ist.
Die beiden ersten Vortheile der Tangential-Turbine sind es, welche sie
besonders für Gebirgsbäche tauglich machen.
Bei diesen Gebirgsbächen hat man oft Gelegenheit, das zu benützende Gefälle beliebig
zu steigern, muß sich dafür aber eine sehr veränderliche Wassermenge gefallen
lassen. Wie es möglich ist, die genannten Vortheile durch eine
Tangential-Turbine zu erreichen, werde ich im Nachfolgenden darzuthun
suchen.
Für die Berechnung führe ich folgende Bezeichnungen ein:
H das Gefälle in Metern, gemessen vom oberen
Wasserspiegel bis zum unteren;
h das Gefälle nach Abzug der Gefällsverluste, welche
durch die Reibung des Wassers in der Zuleitungsröhre entstehen, und derjenigen Höhe,
in welcher das Turbinenrad über dem Spiegel des Unterwassers liegt;
Q die Wassermenge in Kubikmetern, welche per Secunde auf das Rad wirken soll;
α der Winkel, welchen die Richtung des
einströmenden Wasserstrahles mit der an den äußeren Radumfang gezogenen Tangente
einschließt;
β der Winkel, unter welchem das erste Element der
Radschaufeln den äußeren Radumfang durchschneidet;
γ der Winkel, unter welchem das letzte Clement
der Radschaufeln den inneren Radumfang durchschneidet;
U die absolute Geschwindigkeit, mit welcher das Wasser
in das Rad eintritt, = √2gh;
u die relative Geschwindigkeit, mit welcher das Wasser
in die Radcanäle eintritt;
u͵ die relative Geschwindigkeit, mit welcher das
Wasser aus den Radcanälen austritt;
ν die Geschwindigkeit eines Punktes am äußeren
Radumfange;
ν͵ die Geschwindigkeit eines Punktes am
inneren Radumfange;
ω die absolute Geschwindigkeit, mit welcher das
Wasser am inneren Radumfange austritt;
r der äußerer͵ der innere
Halbmesser des Rades;
i die Anzahl der Radschaufeln;
i͵ die Anzahl der Canäle eines jeden
Einlaufes;
e die Radtheilung = 2rπ/i;
e͵ = 2r͵π/i;
s die normale Weite der Canäle des Rades am äußeren
Umfange;
s͵ die normale Weite der Canäle am inneren
Radumfange;
σ die normale Weite der Mündung des
Einlaufes;
δ die lichte Höhe des Rades;
ε die Metalldicke der Radschaufeln;
n die Anzahl der Umdrehungen des Rades per Minute;
Nn der in
Pferdekräften à 75 Kilogrammmetern ausgedrückte
Nutzeffect, welchen die Turbine entwickeln soll.
Es sey BA (Fig. 1) die Richtung des
außen einströmenden Wassers. Das Wasser soll ohne Geschwindigkeitsverlust, also ohne
Stoß in das Rad eintreten und ohne absolute Geschwindigkeit am inneren Umfange des
Rades austreten. Trägt man von A aus auf AB die Größe der Geschwindigkeit des einströmenden
Wassers und auf der Tangente AD die Größe der
Umfangsgeschwindigkeit des Turbinenrades auf und vervollständigt das Parallelogramm
ABCD, so gibt CA die Größe und Richtung der relativen Geschwindigkeit des einströmenden
Wassers an.
Soll nun das Wasser ohne Stoß eintreten, so muß die Richtung des ersten
Schaufelelementes mit der Richtung von AC
zusammenfallen, also mit der Tangente den Winkel β einschließen. Unter den drei Geschwindigkeiten müssen also
folgende Beziehungen stattfinden:
u = √(U² + v² – 2 Uv cos
α) (a)
U/v = sin β/sin (β – α)
(b)
U/u = sin β/sin α
(c).
Sind die Radschaufeln nach einer stetigen Curve gekrümmt, und sieht man von dem
Geschwindigkeitsverluste ab, welcher durch die Reibung des Wassers im Rade und durch
sonstige Störungen in der Bewegung des Wasserstrahles verursacht wird, so ist klar,
daß sich das Wasser in der Schaufelcurve mit einer constanten Geschwindigkeit u fortbewegen würde, wenn die letztere nicht durch die
von der Raddrehung erzeugte Centrifugalkraft verzögert würde.
Diese Centrifugalkraft consumirt aber eine Wirkung = 1000 Q (v² – v²)/2g Kilogrammmeter, also ist unter
dieser Voraussetzung:
Textabbildung Bd. 152, S. 87
oder:
u͵ = √(u² – v² + v͵²) (d).
Der Effectverlust, welcher durch die Störungen in der Bewegung des Wassers beim
Durchgange durch das Rad entsteht, ist indeß so groß, daß er nicht vernachlässigt
werden darf. Berücksichtigt man denselben nicht, so ist klar, daß man nicht die in
der Rechnung vorausgesetzte Umfangsgeschwindigkeit des Rades erhalten wird, und daß
deßhalb der Winkel βgrößer gemacht wird, als es
erforderlich ist, um das Wasser ohne Stoß eintreten zu lassen.
Wie groß übrigens dieser Effectverlust ist, kann durch Rechnung nicht ermittelt,
sondern muß durch Versuche mit gut construirten Tangentialrädern bestimmt werden.
Vorläufig möge derselbe k Procent des theoretischen
Effectes betragen oder = k (1000Qu²)/2g seyn.
Dieß in obige Gleichung eingesetzt, gibt:
Textabbildung Bd. 152, S. 88
oder:
u͵ = √[(1 – k) u² – v² + v͵²] (e).
Trägt man nun in der Verlängerung des letzten Schaufelelementes (Fig. 1) von E nach H die Größe der
relativen Austrittsgeschwindigkeit u, und auf der
Tangente des Radkreises von E nach G die Geschwindigkeit des inneren Radkreises auf, so
erhält man durch Vervollständigung des Parallelogrammes EFGH die absolute Geschwindigkeit, mit welcher das Wasser das Rad verläßt,
nämlich ω = EF
oder:
ω = √(v͵² + u͵² – 2
v͵u͵ cos γ) (f).
Den größtmöglichen Nutzeffect kann man sich nun von dem Rade versprechen, wenn das
Wasser seine Geschwindigkeit ganz an das Rad abgibt, also mit gar keiner absoluten
Geschwindigkeit austritt, oder wenn ω = 0 wird.
Vermöge der Gleichung (f) wird aber ω = 0, wenn cos
γ= 1 oder γ = 0 und u͵ = v͵ wird.
Aus constructiven Gründen kann aber γnicht = 0 gemacht werden, weßhalb man
sich hier einen kleinen Effectverlust von 1000Qω²/2g Klgrmtr. gefallen lassen,
und sich dann begnügen muß, denselben so klein als möglich zu machen, indem man den
Winkel γ möglichst klein und u͵ = v͵
macht.
Damit aber u͵ = v͵ werde, muß nach Gleichung (e): v = u √(1 –
k) gemacht werden, oder wenn man √(1 –
k) = B setzt: v = u B.
Dieß in Gleichung (b) substituirt, gibt: U/u = (B sin β)/sin (β – α),
und da nach Gleichung
(c): U/u = sin β/sin α ist, so erhalten wir die Gleichungen:
sin (β – α) = B sin α
(g)
v = BU sin α/sin
β (h)
n = 60.v/2rπ = 42,2936 B √h/r . sin
α/sin β (i).
Ueber die absolute Größe des Winkels α ist aus den
bisherigen Bedingungsgleichungen noch nichts zu entnehmen, vielmehr ist derselbe
noch vollständig willkürlich. Erst aus einer Betrachtung der
Querschnittsverhältnisse der Radcanale läßt sich ein Anhaltspunkt für die
zweckmäßigste Wahl desselben finden. Es ist nämlich einleuchtend, daß, wenn das
Wasser, welches von Außen in die Radcanäle eintritt, ungezwungen am inneren Umfange
des Rades austreten können soll, unter den beiden Endquerschnitten der Radcanäle
folgendes Verhältniß stattfinden muß:
sδu = s͵δ͵u͵ (k.)
Bei einer feinen Schaufeltheilung und verhältnißmäßig großem Radhalbmesser ist
annähernd (Fig.
2): s = e sin
β = 2rπ/i
sin β, und s͵ = 2r͵π/i sin γ. Dieß in Gleich. (k) substituirt, gibt: ru sin β= r͵u͵ sin γ, und da u = v/B und u͵ = v͵ ist und sich die Umfangsgeschwindigkeiten wie
die Radien verhalten, so erhält man für β
folgende Gleichung:
sin β = (r͵/r)² B. sin γ.
Der Winkel γ, sollte nun aber nach unsern früheren
Entwickelungen möglichst klein genommen werden, indem sonst das Wasser mit zu großer
absoluter Geschwindigkeit aus dem Rade austritt, und r͵/r sowie B sind ächte Brüche; mithin soll β noch
viel kleiner als γ genommen werden, also
jedenfalls auch so klein als möglich. Eine weitere Folgerung glaube ich aus dieser
Betrachtung nicht ziehen zu dürfen, da man der Gleichung (k) durch eine zweckmäßige Anordnung der Schaufelcurven und dann noch
Genüge leisten kann, wenn β = oder größer als γ ist.
Außerdem steht β in einer ganz bestimmten
Beziehung zum Winkel α, und dieser läßt sich aus
constructiven Gründen nicht gut kleiner als 8 bis 9 Grad machen; man ist also in der
Befolgung obiger Weisung sehr beschränkt. Nimmt man z.B. Winkel α = 9° und k =
30 Procent, also
B = 0,8366, so wird vermöge der Gleichung (g) β = 16°30'.
Viel kleiner wird β keinesfalls zu machen seyn.
Nehmen wir daher diesen Werth von β als den
kleinsten an und lassen dabei die Gleichung sin β
= (r͵/r)² B.
sin γ, bestehen, so wird γ = 37°9', wenn man nämlich r͵/r = 3/4 setzt. Der
Effectverlust 1000Qω²/2g wird dann aber schon nahe 5 Proc. des absoluten
Effectes der Wasserkraft, was jedenfalls zu viel ist. Ich nehme daher β so klein als möglich, und ebenso γ, und leiste der Gleichung (k) durch die Curvenconstruction Genüge, worüber später
das Erforderliche gesagt werden wird.
Hier bemerke ich nur noch, daß, wenn man
s = 2rπ/i sin β – ε
(l)
macht, nach Gleichung (k):
s͵ = [2rπ/i sin β – ε.] r/(r͵ . B ) (m)
seyn muß.
Der Querschnitt der Einlaufsmündung bestimmt sich folgendermaßen: Derselbe muß so
groß gemacht werden, daß gerade so viel Wasser durchläuft als man zur Zeit zur
Disposition hat oder nehmen will. Es muß also Uδσ = Q, oder wenn man, wie es
für den guten Gang des Rades zweckmäßig ist, demselben zwei diametral
gegenüberstehende Einläuft gibt: Uδσ = Q/2 gemacht werden.
Bezeichnet man mit S (Fig. 3) die Sehne des
Bogens AB, welcher der Einlaufsmündung entspricht,
und mit x den Winkel, welchen die Tangente AE mit dieser Sehne einschließt, so ist:
σ = S sin (α + x) = S (sin α cos x + cos α sin x).
Da es nun der guten Leitung des Wassers wegen nicht rathsam ist den Bogen AB im Verhältniß zum Radius des Rades sehr groß zu
machen, so ist x stets ein sehr kleiner Winkel, und
ebenso ist Winkel α nach dem Vorhergehenden stets
sehr klein, so daß man annähernd σ = S (sin α + sin x) darf. Es ist aber sin
x = S/2r,
mithin:
σ = S (sin α + S/2r)
(n)
und
UδS (sin α +
S/2r) = Q/2.
In dieser Gleichung sind zwei Größen, nämlich δ
und S zu bestimmen, weßhalb es nothwendig ist, das
Verhältniß derselben zu einander anzunehmen. Es sey daher δ/S = m
bekannt; dieß in die Gleichung substituirt, gibt:
U δ²/m (sin α + δ/2mr) = Q/2
oder:
δ³ + 2mr sin αδ² – m²rQ/U =
0 (o).
Für den Fall, daß m = 1 ist, erhält man:
δ³ + 2r sin
αδ² – rQ/U = 0.
Ist die Wassermenge so groß, daß man es für zweckmäßig halten muß, jeden der beiden
diametral gegenüberstehenden Einläufe durch Leit-Curven oder Wände in i, Abtheilungen zu theilen, so hat man in die Gleichung
(o) für Q͵ Q/i͵ einzuführen, und
bekommt dann für jede Abtheilung des Einkaufes die Gleichung:
δ³ + 2mr sin
αδ² – m²rQ/Ui͵ =
0 (p).
Zur Construction der Turbine bleibt uns jetzt noch die Bestimmung des Radhalbmessers
und die Anzahl und Form der Schaufeln übrig.
Obige Gleichungen und Regeln geben uns über die Größe des Radhalbmessers keinen
Aufschluß, indem das Güteverhältniß der Turbine im Allgemeinen unabhängig von
demselben ist. Wir haben es daher in der Hand, durch eine zweckmäßige Wahl des
Radhalbmessers, die Anzahl der Umdrehungen des Rades ganz dem jedesmaligen Zwecke
anzupassen.
Nach Gleichung (i) ist nämlich:
n = 60.v/2rπ = 42,2936 B √h/r . sin
α/sin β,
also:
r = 42,2936 B √h/n . sin α/sin β
(r).
Man muß jedoch bei der Wahl des Halbmessers immer in gewissen Gränzen bleiben, indem
ein zu großer Halbmesser das Rad schwerfällig und theuer, und ein zu kleiner
Halbmesser die Construction der Schaufeln schwierig und die Anzahl der Umdrehungen
leicht zu groß macht.
Auch ist klar, daß wenn man den Halbmesser sehr klein macht, die Breite des
Radkranzes also r – r͵ klein und mithin
auch die Krümmung der Radschaufeln eine sehr rapide werden muß, was dem
Güteverhältnisse der Turbine sehr nachtheilig ist.
Durch eine gehörige Erwägung aller dieser Umstände kann es indeß nicht schwer fallen,
bald das Rechte zu finden, besonders wenn man sich die Mühe nimmt, mehrere Annahmen
für r aufzuzeichnen und zu vergleichen. Das Verhältniß
von r͵ zu r muß
ebenfalls dem Gutachten des Constructeurs anheim gestellt bleiben. Man erhält
übrigens im Allgemeinen gute Verhältnisse, wenn man für Räder von 1 Meter
Durchmesser und darüber: r͵/r = 3/4 und für Räder unter 1 Meter Durchmesser r͵/r = 2/3 macht.
Um einen gewissen Anhaltspunkt für die Wahl des Radhalbmessers zu haben, kann man
dafür auch eine empirische Regel aufstellen.
Es ist nämlich klar, daß der Halbmesser des Rades sowohl mit wachsender Gefällshöhe,
als auch mit zunehmender Wassermenge größer genommen werden muß, und daß derselbe
daher von der Anzahl der Pferdekräfte, für welche die Turbine construirt wird,
abhängig gemacht werden kann.
Nimmt man an, daß das Güteverhältniß der Turbine = 60 Proc. ist, so ist:
Nn = Qh/0,125 (r*).
In dem oben genannten Aufsatze von Bornemann ist für große
Räder, bei welchen r͵/r = 3/4 gesetzt werden soll, r͵ =
0,0296 Nn, und
für kleine Räder, bei welchen r͵/r =2/3 zu machen ist, r͵ = 0,248 Nn gesetzt. Diese Regel füge ich hier als
Anhaltspunkt für die Wahl des Radhalbmessers und auf den äußeren Radhalbmesser
reducirt, hinzu:
für r͵/r =
3/4 ist r = 0,0395 Nnfür r͵/r = 2/3
ist r = 0,0372 Nn
(s)
Die Anzahl der Radschaufeln muß eine möglichst große seyn, denn je mehr Schaufeln
vorhanden sind, desto besser wird das Wasser geleitet, und desto näher kommen obige
für einen Wasserstrahl aufgestellte Gleichungen der Wahrheit. Auch hiefür
kann man eine empirische Regel aufstellen. Denn setzt man fest, daß:
ε = (r +
0,52)/260 (t)
und:
s = (1,2 + r)/120
(u)
seyn soll, wobei ε nicht
unter 2mm und s
nicht unter 1cm werden kann, übrigens aber
beide mit wachsendem Halbmesser zunehmen, und daß der Winkel β nicht sehr von 18° verschieden ist, so erhält man für die
Anzahl der Radschaufeln die empirische Regel
Textabbildung Bd. 152, S. 93
Die Krümmung der Radschaufeln soll eine solche seyn, daß das durchströmende Wasser
keine plötzlichen Geschwindigkeitsänderungen erleide, daß das erste Element der
Krümmung mit dem äußeren Radkreise den Winkel β,
und daß das letzte Element derselben mit dem inneren Radkreise den Winkel γ einschließe.
Die vortheilhafteste Krümmung wäre allerdings diejenige, bei welcher die absolute
Bewegung des Wassers eine gleichförmig verzögerte ist, allein eine geringe
Abweichung von dieser vortheilhaftesten Krümmung wird noch keinen wahrnehmbaren
Effectverlust verursachen. Ich mache daher hievon in so ferne eine Abweichung, als
ich Sorge getragen habe, bei gleicher innerer und äußerer Radhöhe den Anforderungen
der Gleichung (k) Genüge zu leisten, und dabei den
Winkel γ möglichst klein zu bekommen (Fig. 4).
Außerdem setze ich die Schaufelcurve aus vier Kreisbögen zusammen, deren Halbmesser
mit ρ₁, ρ₂, ρ₃
und ρ₄ bezeichnet werden mögen. Den Radius
ρ₁ des ersten Schaufelstückes habe ich
so gewählt, daß die normale lichte Weite s am Eingange
der Canäle für die Ausführung stets genügend genau = 2rπ/i sin β – ε werde.
Zur Erfüllung dieser Bedingung ist es nothwendignoihwendig:
ρ₁ = r
– (2rπ sin β)/i
(v)
zu machen, da AC₁ nahe
gleich r und AG = (2rπ sin β)/i
ist. Die Mittelpunkte dieser ersten Curvenelemente fallen in einen Kreis welcher mit
dem Radius CC₁ = 2r sin
β/2 aus dem Mittelpunkte C des Rades
beschrieben ist.
Schneidet man also diesen Kreis von B aus mit dem Radius
BC₁ = ρ₁, so hat man damit den Mittelpunkt C₁ ohne Weiteres gefunden. Die Länge des ersten Curvenstückes wird
in G durch die Verbindungslinie AC₁ abgeschnitten.
Das Ende einer jeden Schaufel lasse ich in den durch den Anfangspunkt der
nächstfolgenden Schaufel gezogenen Radius fallen. Denn einmal nähere ich mich
dadurch der theoretisch besten Krümmung, welche eine sackförmige ist; und anderseits
kann man hiebei den Winkel γ noch ziemlich klein
halten ohne der Gleichung (k) Abbruch zu thun, und ohne
den letzten Radius ρ₄ zu klein nehmen zu
müssen.
Der Radius ρ₄ läßt sich berechnen. Denn
zunächst kann man den Centriwinkel C₄ finden,
welcher dem letzten Bogenstücke ED der Schaufel
entspricht.
Zieht man nämlich die Halbirungslinie des Winkels C₄ bis F, d.h. bis zum Durchschnitt mit der
in E an das Bogenstück ED gezogenen Tangente, bezeichnet man EF
mit a͵ EH = (2r͵π)/i mit e͵, setzt DH = s͵ + ε = b und den Winkel
180/i = x ist
zunächst:
Textabbildung Bd. 152, S. 94
und
Textabbildung Bd. 152, S. 94
Hat man auf diese Weise den Winkel C₄ berechnet,
so ist:
Textabbildung Bd. 152, S. 94
Auch die beiden anderen Krümmungshalbmesser ρ₂ und ρ₃ lassen sich
alsdann berechnen. Die Berechnung derselben ist indeß so weitläufig, daß sie keinen
praktischen Werth hat, indem man durch Probiren viel schneller zum Ziele kommt.
Ebenso findet man den Radius ρ₄ leichter
durch Versuche. Trägt man nämlich in E den Winkel γ + 90 an die Tangente des inneren Radkreises, so
erhält man die Linie EC₄. Beschreibt man
ferner um den Punkt H einen Kreis mit dem Halbmesser
(s͵ + ε)
und sucht dann einen Kreis auf, welcher letzteren Kreis berührt und dessen
Mittelpunkt in der Linie EC₄ liegt, so hat man
die Aufgabe gelöst.
Den Winkel γ bei dieser Anordnung kleiner als
18° zu machen, ist nicht rathsam, weil sonst das letzte Schaufelstück zu
stark gebogen wird. Nach
diesen Erörterungen ist es nothwendig die gewonnenen Resultate hier in Kürze
zusammen zu stellen:
1. Nn = Qh/0,125.
2. U = √2gh.
3. α möglichst klein, etwa
9°.
4. sin (β – α) = B sin α.
5. v = BU sin
α/sin β.
6. u = U sin
(β – α)/(B sin β).
7.
Für Nn
≧ 15 : r = 0,0359 NnFür Nn
< 15 : r = 0,0272 Nn
oder
8. r = 42,2936 . B √h/n . sin α/sin β.
9.
bei r ≧ 0,5m : r͵ = 3/4rbei r < 0,5m : r͵ = 2/3r
10. i = 2940/(19 + 18,18/r).
11. ε = (0,52 + r)/260.
12. s = 2rπ/i sin β – ε.
13. s͵ = s r/Br͵.
Bei zwei einfachen diametralen Einläufen:
14. δ³ + 2 mr sin αδ² – m²rQ/U = 0.
15. m = δ/S; (m
etwa = 1).
Bei zwei Einläufen, jeder mit i͵ Abtheilungen:
16. δ³ + 2 mr sin αδ² – m²rQ/Ui͵ =
0.
17. v͵ = r͵/r . v =
u͵,
18. γ möglichst klein, etwa =
18° 30',
19. ω = √(v͵² + u͵² – 2
v͵u͵ cos γ),
20. B = 0,8366 (bis Erfahrungsresultate vorliegen).
Um den Gebrauch dieser Formeln zu erläutern, möge hier ein Beispiel gerechnet
werden.
Es sey gegeben:
1. das totale Gefälle H = 13m,86;
2. Q = 0,15 Kubikmeter.
Der Durchmesser der Zuleitungsröhre werde
D = √(4Q/π) = 0m,43
genommen und die Länge derselben sey L = 120m.
Dann beträgt der Gefällverlust durch Reibung in dieser Röhre:
z = 4L/Q . 0,0003656 = 0m,408.
Die mittlere horizontale Ebene des Turbinenrades liege 45ctm über dem Spiegel des Unterwassers, so
daß das nutzbare Gefälle h = 13m bleibt.
Alsdann erhalten wir:
Nn = Qh/0,125 = 15,6 Pferdekräfte,
U = √(19,611 . 13) = 15m,968,
α = 9°; sin
(β – α) – 0,1564 .
0,8366 = 0,1308,
β = 16° 30',
γ = 18° 30',
v = 0,8366 . 15,968 . 0,1564/0,2840 = 7m,357,
u = U sin(β – α)/(B . sin α) = v/B = 8m,793,
r = 0,0395 . 15,6 = 0m,616,
r͵ = 3/4 . 0,616 = 0m,462,
n = 35,383 . √(13/0,616) . 0,1564/0,2840 =
114
i = 2940/(19 + 18,18/0,616) = 61 dafür i = 60,
e = (2rπ)/i = 0m,0645,
ε = (0,616 + 0,52)/260 = 0m,004
s = 0,0645 . 0,284 – 0,004 = 0m,015,
s͵ = 0,015 . 3/4B = 0m,024,
m = 1
δ³ + 0,193δ² – 0,00578 = 0,
daraus:
δ = 0m,133,
S = 0m,133,
σ = 0,133 (0,1564 + 0,133/1,23) = 0m,035,
ρ₁ = r
– (2rπ sin β)/i – ε = 0m,5967,
und
CC₁ = 2r sin
½ β = 0m,176.
Zur Berechnung des Krümmungshalbmessers ρ₄
ist:
e͵ = 2r͵π/i = 0m,0484
b = (s͵ + ε) = 0m,028,
Winkel (x + γ) = 3° + 18° 30' = 21° 30'.
Dann ist nach Gleichung (w):
a = 0m,0178;
nach Gleichung (x):
C₄ = 27° 33', und nach Gleichung (y):
ρ₄ = 0m, 073.
Durch Probiren erhält man alsdann:
ρ₂ = 0m,09, und ρ₃ = 0m,07.
Ein oberschlächtiges Rad für das Gefälle von 13m und eine Wassermenge von 0,15 Kubikm. würde, nach den
„Resultaten für den Maschinenbau von Redtenbacher,“ einen Durchmesser von 12m,546, und eine Breite von 1m,63 erhalten. Die Anzahl der Radarme würde
= 27, die der Schaufeln = 108 und die der Umdrehungen per Minute = 0,43 seyn, woraus hinreichend ermessen werden kann, daß das
Wasserrad ein höchst schwerfälliges und unzweckmäßiges werden würde.
Wollte man dagegen statt dessen eine Jonval'sche
Vollturbine construiren, so erhielte man nach demselben Buche, §. 216, einen
äußeren Halbmesser von
0m,228 und 452 Umdrehungen per Minute, was für die Ausführung jedenfalls sehr
bedenklich und für die Erhaltung des Turbinenzapfens sehr gefährlich wäre.
Die Tangential-Turbine ist daher beiden entschieden vorzuziehen.
Aus der Betrachtung der für den günstigsten Nutzeffect aufgestellten Gleichungen geht
nun hervor, daß das Güteverhältniß der Turbine bei veränderlicher Wassermenge Q dasselbe bleiben muß, wenn man nur im Stande ist die
Einströmungsgeschwindigkeit U und den Einströmungswinkel
α stets constant zu erhalten, oder mit
anderen Worten, wenn man im Stande ist, der Gleichung: δσ U = 1/2 Q bei veränderlichem
Q und constantem U stets
zu genügen. Bei einer ausgeführten Turbine ist aber die Radhöhe δ auch constant, man wird daher der obigen
Anforderung entsprechen, wenn man den Einlauf so construirt, daß seine Weite σ entsprechend verändert werden kann, ohne den
Winkel α dadurch zu verändern.
Dieß kann nun vollkommen durch die im Folgenden beschriebene Construction des
Einlaufes erreicht werden.
Fig. 5 ist der
Verticaldurchschnitt des Einlaufes nach der Linie XY und Fig. 6 der Horizontaldurchschnitt desselben.
C, D, E, F, A (Fig. 6) ist die äußere
Wand des Einlaufkastens. Das Stück C, D ist fest mit E, F, A verschraubt und kann, wie überhaupt der ganze
Einlauf, seine Lage gegen das Rad nicht verändern. Der Theil C, D der Einlaufswand ist ferner genau nach einem aus dem Mittelpunkte des
Turbinenrades beschriebenen Kreise gekrümmt und glatt bearbeitet. An dieses Stück
C, D legt sich die Schütze B,
G genau an. Diese Schütze ist ein aus Metall gearbeiteter Kasten, welcher
bei B in eine Spitze ausläuft und folgendermaßen geformt
ist: Die dem Turbinenrade abgekehrte Verticalwand bildet nach der Spitze B zu eine Ebene, welche mit der in B an das Rad gezogenen Tangential-Ebene den
Winkel α einschließt, und geht gegen das Ende G
in einen aus dem Mittelpunkte des Rades beschriebenen Kreis über. Die innere Wand
des Schützenkastens ist ebenfalls mit dem Turbinenrade concentrisch gekrümmt und
innerhalb mit einer ebenso gebogenen kleinen Zahnstange c,
d versehen. In diese Zahnstange greift das kleine Getriebe b der Welle e. Die Welle e wird durch eine Pfanne h
im Boden des Einlaufkastens und durch eine Stopfbüchse im Deckel desselben gehalten
und tritt vermittelst zweier mit dem Turbinenrade concentrisch gebogenen Schlitze
a, a durch den Boden und Deckel des Schützenkastens.
Durch Drehung der Welle e und des Zahnrades b kann somit die Schütze in dem Einlaufkasten bewegt
werden und zwar muß diese
Bewegung mit dem Umfangskreis des Turbinenrades concentrisch geschehen.
Die Einlaufslinie HB wird daher mit der Radtangente
stets den Winkel α einschließen, in welcher
Stellung die Schütze sich auch befinden mag.
Bewegt man die Schütze so weit nach Vorwärts, daß der Punkt B mit dem Punkte A zusammenstößt, so ist der
Einlauf ganz geschlossen und die Linie BH wird
alsdann ganz mit der Linie AK zusammenfallen,
indem die Wand AF ebenfalls mit dem Umfange des
Rades den Winkel α einschließen muß.
Durch den Druck des Wassers kann die Schütze nicht aus ihrer Lage gebracht werden, da
dieselbe durch die Wand C, D, die Welle e und das Zahnrad b gehalten
wird. Man hat es also durch eine richtige Drehung der Welle e in der Gewalt, die Weite σ des
Einkaufes ganz der Wassermenge anzupassen, ohne die Richtung des einströmenden
Wasserstrahles dadurch zu verändern, und hiedurch auch bei sehr veränderlicher
Wassermenge stets dasselbe Güteverhältniß zu erreichen.
Ist die Wassermenge so groß, daß die Bogenweite der Einlaufsmündung erheblich größer
als zwei Schaufeltheilungen des Turbinenrades, oder daß S erheblich größer als 2 e wird, so muß man
den Einlauf durch Scheidewände in Abtheilungen theilen. Diese Scheidewände stehen
fest und schließen alle mit der jedesmaligen Radtangente den Winkel α ein. Oben beschriebene Schützenconstruction
wird alsdann nur bei dem inneren Einlaufscanale angewendet, während die übrigen
Einlaufscanäle durch einen anzubringenden einfachen geraden Schieber verschließbar
zu machen sind.
Bei Fig. 5 und
6 habe ich
die Dimensionen des oben gerechneten Beispiels zu Grunde gelegt.
Tafeln