| Titel: | Theorie eines Ovalwerkes; von Georg Wellner in Prag. |
| Autor: | Georg Wellner |
| Fundstelle: | Band 184, Jahrgang 1867, Nr. XXVI., S. 120 |
| Download: | XML |
XXVI.
Theorie eines Ovalwerkes; von Georg Wellner in Prag.
Mit Abbildungen auf Tab.
III.
Wellner, Theorie eines Ovalwerkes.
Die Mechaniker haben bekanntlich Vorrichtungen ersonnen, um ebenso wie man auf
gewöhnlichen Drehbänken Arbeitsstücke kreisrund abzudrehen vermag, ovale oder
elliptische Querschnitte zu erzeugen. So verschieden die Constructionen dieser
Ovalwerke sind, kommen sie doch alle darin überein, daß neben der Rotation auch eine
lineare Oscillationsbewegung um ein Centrum stattfinden muß.
Eine dieser Unordnungen, wie ich sie beim Kunstmechaniker Fr. Bozek in Prag angetroffen habe, functionirt äußerst sicher, ist sehr
compendiös und soll nun im Principe erläutert werden.
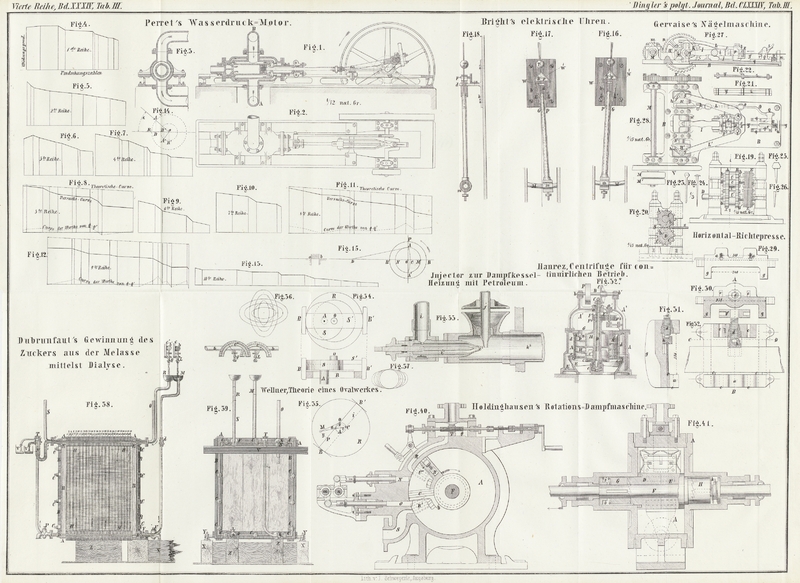
Ein Ring R, Figur 34, läßt sich durch
eine Schraube (welche in der Zeichnung weggelassen ist) gegen die fix gelagerte
Achse A in excentrische Lage bringen. Centrisch auf
dieser Achse sitzt die Scheibe S, in deren Nuth sich ein
Schieber S' hin- und herbewegt. An seinen Enden
trägt derselbe zwei Backen B und B', welche den excentrischen Ring R umgreifen
und auf diese Weise bei Drehung der Scheibe ein Verschieben des Mittelpunktes O bezwecken. In O wird nun
der oval zu drehende Gegenstand eingespannt, so daß er neben einer Drehung auch eine
Verrückung längs des Schiebers erleidet.
Der Meißel ist in M, Fig. 35, angebracht und
läßt sich sein horizontaler Abstand (a) von der Achse
A durch eine Schraube abändern. Die Excentricität
des Ringes R, d.h. die Entfernung seines Mittelpunktes
C von der Achse A sey
e genannt.
Wie leicht einzusehen ist, durchläuft nun das Centrum O
des Schiebers S' während der Rotation einen zwischen A und O beschriebenen Kreis
vom Radius e/2, ohne jemals auf die zweite Seite der
Achse zu kommen. – Der in einem Support befestigte Stichel behält hierbei
seine Stellung in M und greift stets neue Punkte des ihm
dargebotenen Gegenstandes an. Der variable Abstand dieser Punkte (M) von dem im Kreise sich fortbewegenden Centrum O ª wird sich als radius
vector der entstehenden Curve darstellen und variirt, wie aus Figur 35
ersichtlich ist, zwischen den Werthen « = a. und
MC
= a + e.
Wählt man nun O zum Anfangspunkt der Coordinaten und die
Schieberrichtung OA zur x-Achse, so findet sich durch einfache Rechnung aus den
rechtwinkligen Dreiecken MPA und AOC die Relation:
a² (a + e)² = (a + e)² y² + a² x². (1)
Es ist dieß die Gleichung der vom Stichel eingeritzten Curve, bezogen auf den
Mittelpunkt O des Arbeitsstückes.
Die Gleichung liefert Ellipsen mit den Halbachsen a + e und a.
Wenn man demnach bei irgend einer Stellung des excentrischen Ringes (also bei
gegebenem e) den Stichel in horizontaler Richtung
verrückt (d.h. a verändert), so entsteht ein System von Ellipsen, deren
Halbachsen stets um ein Gleiches, nämlich um e,
differiren.
Für a = 0, d.h. wenn man den Stichel in der
Achsenrichtung selbst festspannt, geht die Gleichung (1) über in: y = 0. Die Ellipse wird zu einer begrenzten Geraden von
der Länge e.
Wenn a negativ wird (= – a₁), d.h. der Stichel auf die zweite Seite der Achse zu stehen
kommt, schreibt sich die Ellipsen-Gleichung: a₁² (e – a¹)² = (e
– a₁)² y² + a₁² x²; die horizontale Halbachse e – a₁ wird
immer kleiner, während sich die Verticalachse a₁
wieder hebt.
Bei a = – e/2
entsteht: e²/4 = y² + x², ein Kreis vom Radius e/2, bis für a = –
e die sich vertical stellende Ellipse wieder zur
Geraden wird, um bei noch weiterer Verrückung in vertical stehende Ellipsen
überzugehen; siehe Figur 36.
Wenn man bei unverrücktem Meißel (also konstantem a) den
excentrischen Ring in verschiedene Lagen bringt (d.h. e
variiren läßt), so entsteht ein Bild, wie es Figur 37
versinnlicht.
Für centrisch gestellten Ring (e = 0) wird aus der Formel
(1) a² = x² +
y² d. i. Gleichung eines Kreises, dessen
Radius dem Abstande des Meißels vom Wellenmittel entspricht.
Will man somit einen bestimmten Ellipsen-Querschnitt mit den Halbachsen A und B erzielen, so
entferne man den Meißel von der Achse um die Länge A und
verschiebe hierauf den excentrischen Ring (so weit, daß seine Excentricität = A – B beträgt, also)
um die Differenz der Halbachsen von seiner Mittelstellung.
Alle diese Betrachtungen gelten nur dann, wenn der Stichel in einer Horizontalen
(nämlich in der Richtung der Excentricität) beweglich ist. Für höher oder tiefer
gelegene Punkte ändert sich die Beziehung der Coordinaten, man erhält keine Ellipsen
mehr, sondern transcendente in sich zurückkehrende Curven.
Ich glaube im Vorstehenden die theoretische Seite eines Ovalwerkes hinreichend
beleuchtet zu haben, um behaupten zu können, daß die praktische Verwerthung der
mathematischen Resultate sehr leicht zu ermöglichen ist. Man soll sich eben beim
Ovaldrehen nicht – wie so häufig geschieht – damit begnügen, daß die
Maschinerie irgend ein Oval verzeichnet, sondern man soll im Voraus wissen und
bestimmen, was für ein Oval verzeichnet werden muß.
Tafeln