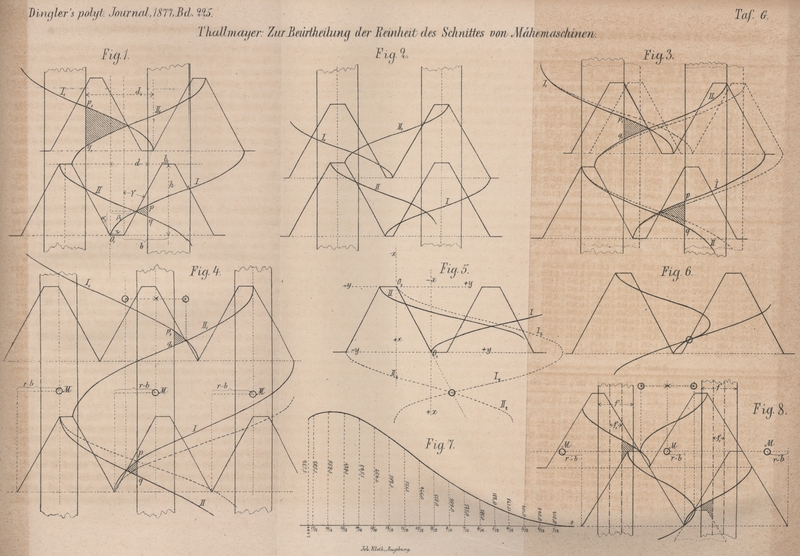
| Titel: | Zur Beurtheilung der Reinheit des Schnittes bei Mähemaschinen; von Prof. V. Thallmayer. |
| Autor: | V. Thallmayer |
| Fundstelle: | Band 225, Jahrgang 1877, S. 523 |
| Download: | XML |
Zur Beurtheilung der Reinheit des Schnittes bei
Mähemaschinen; von Prof. V.
Thallmayer.
Mit Abbildungen auf Texttafel G.
Thallmayer, über die Reinheit des Schnittes bei
Mähemaschinen.
In der frühern Abhandlung (Bd. 224 S. 573) wurden zur Bestimmung der Strecke pq (des Vorwärtsbiegens) die Formeln 3 und 10
aufgestellt; daselbst ist jedoch nur das Vorwärtsbiegen für den Messerhub von links
nach rechts in Betracht gezogen. Es geben aber diese Formeln, wie dies auch aus Figur 1
Texttafel G zu entnehmen, wenn darin statt d der Werth d₁,
eingesetzt wird, das Vorwärtsbiegen p₁q₁ für den darauffolgenden Messerhub von rechts
nach links. Die Gleichheit zwischen pq und p₁q₁ ist an
die Gleichheit d und d₁ gebunden. In Figur 1 ist d nicht gleich d₁,
daher auch p₁q₁ von pq verschieden. Die Gleichheit
von pq
undnnd
p₁q₁ tritt,
wie in Figur
2, stets ein, wenn der Messerhub gleich der Fingertheilung ist und die
Messermitten mit den Fingermitten bei auf das Ende des Hubes gestellter Kurbel
zusammenfallen. Durch entsprechende Anfangsstellung der Messerschiene, wobei unter
Anfangsstellung jene verstanden ist, welche sie einnimmt, wenn die Kurbelscheibe am
todten Punkte angelangt ist, kann die Gleichheit der Strecke pq für den Hin- und Rückgang der Messer
erzielt werden (Fig.
3, 4, 8).
Die Erfahrung hat erwiesen, daß durch das Vorwärtsbiegen der Halme –
ausgenommen, es träte auf eine große Ausdehnung ein – die Reinheit des
Schnittes in aufrecht stehendem Getreide nicht wesentlich beeinträchtigt wird; doch
erscheint es, um auch bei gelagertem Getreide einen reinen Schnitt zu erzielen,
immerhin wünschenswerth, die Mähemaschinen so anzulegen, daß das Vorwärtsbiegen der
Halme nur innerhalb enger Grenzen eintreten könne und wo möglich gleich Null werde.
Um einen Ausgangspunkt zur Bestimmung von diesen Bedingungen entsprechenden
Dimensionen für Mähemaschinen zu gewinnen, erscheint es nicht unzweckmäßig, solche
zusammengehörige Werthe von Ψ und w ins Auge zu fassen, für welche der Schnittpunkt der
Curven I und II grade auf die Messerkante fällt (Fig. 1, 3, 4, 8). Für diesen Fall
nämlich sinkt das Vorwärtsbiegen schon auf eine ziemlich unbedeutende Ausdehnung
herab, und es kann wenn nothwendig noch auf eine geringere Ausdehnung herabgemindert
werden und zwar, wie in Figur 4, durch
Vergrößerung des Uebersetzungsverhältnisses n. (In Figur 4
entsprechen die punktirt ausgezogenen Curven einem größern Uebersetzungsverhältnisse
als die voll ausgezogenen.) Durch Vergrößerung des Messerhubes gewinnt man, wie sich bei etwas
aufmerksamer Betrachtung von Figur 3 ergibt, in dieser
Beziehung nichts.
Die Relation, welche zwischen ψ und w bestehen muß, damit der Schnittpunkt der Curven I und
II grade auf die Messerkante falle, ist, wenn man z =
φr und b₁ = δr und der Kürze
halber
Textabbildung Bd. 225, S. 524
Aus Figur 1 bestimmt sich
nämlich für diesen Fall tg γ = (β₁ – z)/α₁ und auch tg γ = (b –
b₁)/h, somit (β₁ – z)/α₁ = (b – b₁)/h oder β₁/α₁ = z/α₁ + (b – b₁)/h. Letztere
Gleichung gibt unter Berücksichtigung der Relationen β₁ = r(1 – Δ), α₁
= v/2π arc cos Δ,
b + b₁ = wr und h = (v/2)ψ unmittelbar die obige Gleichung
(1).
Will man aus Gleichung (1) zu einem bestimmten Werthe von ψ, φ und δ unmittelbar
einen Näherungswerth für w erhalten, so setze man darin
für arc cos Δ seinen Reihenwerth ein. Mit
Vernachlässigung der höhern Potenzen erhält man dann in Bezug auf w eine Gleichung des vierten Grades. So z.B. ergibt sich
neben der Annahme φ = 0,2, δ = 0,05, ψ = 1 zur Bestimmung
von w die Gleichung w⁴ – 12,76 w³ + 51,43 w² – 68,19 w +
28,52 = 0 und aus ihr nebst zwei imaginären Wurzeln die reellen w = 1 und w = –
0,623. Dem verfolgten Zwecke entspricht hierbei die positive Wurzel. Der negative
Werth von w entspricht dem Zusammenfallen des
Durchschnittspunktes der Curven I₂ und II₂ mit der Verlängerung der
Messerkante (Fig.
5), worauf hier nicht reflectirt wird. Die Richtigkeit ergibt sich durch
die Erwägung, daß für O₂ als Ursprung eines
rechtwinkligen Coordinatensystemes y – r = – r cos mx/r die Gleichung der Curve I₂ und y – r + (b + b₁) = –
r cos (mx/r – mh/r) die Gleichung der Curve II₂ ist, welche zwei
Gleichungen sich von den in Bd. 224 S. 577 für die Curven I und II gefundenen
Gleichungen nur dadurch unterscheiden, daß das Vorzeichen von (mh)/r verschieden ist.
Die daselbst S. 578 gefundene Formel 5 gibt aus diesem Grunde auch vier Werthe für
α, nämlich sowohl die Abscissen der
Durchschnittspunkte der Curven I und II mit Bezug auf O₁, als
Coordinatenursprung, als auch die der Durchschnittspunkte der Curven I₂ und
II₂ mit Bezug auf O₂ als
Coordinatenursprung.
Es lassen sich jedoch zusammengehörige Werthe von ψ und w ziemlich leicht und rasch auch
unmittelbar aus Gleichung (1) bestimmen. Dies ist für verschiedene Werthe von δ und φ
geschehen und sind die gewonnenen Verhältnißzahlen in den weiter unten folgenden
Tabellen zusammengestellt worden.
Grenzwerthe für ψ und positive Werthe von w sind erstens w = 0 und der
zugehörige Werth von ψ, der sich aus Gleichung
(1), nachdem darin für w der Werth Null eingesetzt
wurde, bestimmt. Setzt man in Gleichung (1) für w den
Werth Null ein, so übergeht sie in die Gleichung
1 – cos
ψπ/2 = φ – 2δ/ψπ
arc cos (cos
ψπ/2), woraus folgt:
cosψπ/2 = (δ – ῳ + 1) und ψ = (2 arc cos (1 +
δ – φ))/π.
Für Werthe von ψ, die
kleiner sind als die durch die letzte Formel gegebenen, wird w negativ.
Die andern Grenzwerthe für ψ und w entsprechen dem Falle, wo der Berührungspunkt der
Curven I und II auf die Messerkante fällt, wie in Figur 6. Diese letztern
Grenzwerthe für w und ψ ergeben sich aus Gleichung (1), nachdem darin w = 2sin (Ψπ)/2 eingesetzt wurde, was, wie früher
schon gefunden wurde, die Bedingung für das Berühren der beiden Curven I und II ist.
Man erhält so zur Bestimmung von ψ die
Gleichung
Textabbildung Bd. 225, S. 525
welche, um für w auf einfachere
Weise Näherungswerthe zu erhalten, sich leicht auf die Gleichung
Textabbildung Bd. 225, S. 525
bringen läßt. Es erscheinen diese Grenzwerthe in die zwei
letzten Zeilen der Tabellen eingetragen.
Die Tabellen enthalten die Werthe von w, welche den
zwischen 15/12 und 6/12 liegenden Werthen von ψ
entsprechen, was für die Praxis ausreicht. Viele Werthe von w sind nur der Vollständigkeit halber in die Tabellen aufgenommen; denn es
haben jene Werthe von w, welche unter 0,6 fallen,
insofern keine praktische Verwendbarkeit, als sie zu großen Messerhub und damit
erschwerte Geradführung der Messerschiene bedingen.
Der Werth von w nimmt innerhalb der oben erwähnten
Grenzwerthe einmal einen Maximalwerth an, wie man dies auch aus Figur? entnehmen
kann, in welcher die Werthe von w als Ordinaten einer
Curve eingeschrieben erscheinen. Die Curve entspricht der Annahme φ = 0 und δ =
0.
Die Ausarbeitung der Tabellen erleichterte wesentlich der Umstand daß bei einem und
demselben Werthe von ψ für das arithmetische
Mittel φ₂ zweier nicht weit aus einander
liegender Werthe von φ und φ₁ der zu diesem Mittel φ₂ gehörige Werth w₂ auch
nahezu das arithmetische Mittel der den Werthen φ
und φ₁ zukommenden Werthe w und w₁ ist, und daß
bei einem und demselben φ und ψ der dem arithmetischen Mittel zweier nicht weit
aus einander liegender Werthe von δ zukommende
Werth von w nahezu das arithmetische Mittel der den zwei
Werthen von δ zukommenden Werthen von w ist. Dies gründet sich theilweise darauf, daß für
solche Werthe von Δ und Δ₁, welche nicht weit aus einander liegen, (arc cos Δ + arc cos
Δ₁)/2 nahezu gleich arc
cos (Δ +
Δ₁)/2 ist, und daß für Werthe von w und w₁, wenn sie
wenig von einander abweichen,
Textabbildung Bd. 225, S. 526
nahezu gleich
Textabbildung Bd. 225, S. 526
ist.
Bei den jetzt gebräuchlichen, in der Praxis bewährten Mähemaschinen ist v/2 selten größer als 10cm und selten kleiner als 4cm,5. Der Hub des Messers überschreitet
beinahe nie die Größe von 14cm und ist
selten kleiner als 6cm. Der
Fahrraddurchmesser beträgt ungefähr 75cm.
Das Uebersetzungsverhältniß n bei Grasmähemaschinen ist
selten größer als 26 und bei Getreidemähemaschinen selten kleiner als 12; combinirte
Mähemaschinen, d. s. solche, die sowohl zum Gras, als wie auch zum Getreideschnitte
geeignet sind, haben gewöhnlich ein Uebersetzungsverhältniß von 20, oder sie sind so
eingerichtet, daß sich durch Auswechslung eines Zahnrades die Uebersetzungszahl für
den Grasschnitt vergrößern läßt.
Den Werth von z anbelangend, ist es des bequemen
Nachschärfens der Messer wegen erwünscht, daß er größer als Null sei, d.h. die
Messerkanten sollen, wo es angeht, in der Ausdehnung, in welcher sie wirksam sind,
nämlich schneiden, nicht in einem Punkte zusammenstoßen. Ebenso ist es bei der
geringen Dicke der Messerbleche nicht gut möglich, die scharfe Spitze der Messer auf
die Dauer zu erhalten, weshalb man ihnen seltener die Form eines Dreieckes, sondern
meist die eines Trapezes gibt. Der schneidende Theil der Messerhöhe ist selten
größer als 6cm; Messerhöhe und Breite
sollen in einem solchen Verhältniß stehen, daß die schneidenden Kanten der Messer
mit den Fingerkanten keinen zu großen Winkel bilden.
Die Tabellen I bis VI dehnen sich auf die Werthe von φ = 0 bis φ = 0,5, δ = 0,05 bis δ
= 0,2 und ψ = 1/2 bis ψ = 5/4 aus. Die Werthe von ψ
sind von Zwölftel zu Zwölftel fortschreitend angenommen worden; für dazwischen
liegende Werthe von ψ findet sich das zugehörige
w leicht durch Interpolation. Wo sich für w negative Werthe ergeben hätten, sind in die Tabellen
keine Zahlen eingetragen worden.
Tabelle I.
ψ
Werthe von w für
φ = 0 und δ =
Werthe von w für
φ = 0,05 und δ =
0,05
0,075
0,1
0,15
0,2
0,05
0,075
0,1
0,15
0,2
15/12
1,662
1,679
1,700
1,724
1,751
1,585
1,608
1,621
1,650
1,682
14/12
1,590
1,614
1,633
1,666
1,711
1,505
1,525
1,548
1,581
1,624
13/12
1,480
1,503
1,519
1,564
1,618
1,386
1,410
1,434
1,479
1,521
1
1,338
1,366
1,389
1,443
1,493
1,245
1,271
1,297
1,345
1,394
11/12
1,192
1,225
1,275
1,279
1,348
1,091
1,120
1,151
1,189
1,246
10/12
1,032
1,064
1,095
1,146
1,205
0,935
0,958
0,990
1,044
1,098
9/12
0,872
0,903
0,925
0,995
1,061
0,779
0,806
0,833
0,891
0,948
8/12
0,726
0,756
0,786
0,848
0,908
0,630
0,657
0,685
0,742
0,798
7/12
0,582
0,615
0,645
0,711
0,772
0,486
0,515
0,545
0,600
0,656
6/12
0,457
0,486
0,515
0,581
0,641
0,358
0,386
0,415
0,469
0,524
ψ
1,430
1,422
1,413
1,396
1,378
1,487
1,472
1,464
1,450
1,435
w
1,561
1,576
1,593
1,625
1,656
1,442
1,474
1,491
1,521
1,549
Tabelle II.
ψ
Werthe von w für
φ = 0,1 und δ =
Werthe von w für
φ = 0,15 und δ =
0,05
0,075
0,1
0,15
0,2
0,05
0,075
0,1
0,15
0,2
15/12
1,519
1,538
1,579
1,588
1,613
1,448
1,465
1,495
1,516
1,549
14/12
1,423
1,447
1,471
1,515
1,544
1,349
1,370
1,398
1,433
1,472
13/12
1,300
1,325
1,350
1,395
1,434
1,221
1,246
1,271
1,316
1,358
1
1,156
1,185
1,205
1,262
1,310
1,078
1,104
1,129
1,185
1,225
11/12
1,004
1,029
1,055
1,115
1,159
0,919
0,949
0,978
1,025
1,074
10/12
0,845
0,875
0,902
0,955
1,008
0,766
0,805
0,820
0,872
0,921
9/12
0,695
0,722
0,750
0,799
0,851
0,617
0,642
0,667
0,718
0,769
8/12
0,545
0,571
0,600
0,651
0,704
0,470
0,495
0,520
0,573
0,623
7/12
0,403
0,431
0,460
0,512
0,562
0,332
0,360
0,385
0,437
0,484
6/12
0,278
0,305
0,326
0,385
0,431
0,212
0,239
0,263
0,313
0,359
ψ
1,521
1,514
1,507
1,493
1,480
1,558
1,552
1,545
1,533
1,520
w
1,366
1,381
1,396
1,429
1,456
1,277
1,293
1,309
1,338
1,369
Tabelle III.
φ
Werthe von w für
φ = 0,2 und δ =
Werthe von w für
φ = 0,25 und δ =
0,05
0,075
0,1
0,15
0,2
0,05
0,075
0,1
0,15
0,2
15/12
1,379
1,388
1,423
1,445
1,486
1,313
1,333
1,352
1,387
1,423
14/12
1,275
1,297
1,332
1,360
1,400
1,206
1,228
1,251
1,291
1,331
13/12
1,142
1,169
1,198
1,241
1,283
1,072
1,097
1,122
1,167
1,211
1
1,000
1,025
1,055
1,100
1,147
0,928
0,952
0,977
1,026
1,073
11/12
0,330
0,868
0,904
0,943
0,981
0,772
0,799
0,826
0,873
0,919
10/12
0,691
0,716
0,741
0,794
0,841
0,621
0,647
0,672
0,722
0,770
9/12
0,544
0,565
0,585
0,643
0,694
0,471
0,497
0,521
0,573
0,623
8/12
0,391
0,423
0,446
0,500
0,550
0,322
0,357
0,382
0,432
0,480
7/12
0,265
0,290
0,315
0,373
0,415
0,203
0,229
0,254
0,303
0,355
6/12
0,154
0,175
0,202
0,250
0,293
0,094
0,119
0,143
0,150
0,235
ψ
1,593
1,587
1,580
1,568
1555
1,627
1,616
1,615
1,603
1,592
w
1,192
1,208
1,224
1,255
1,286
1,105
1,120
1,136
1,166
1,196
Tabelle IV.
φ
Werthe von w für
φ = 0,3 und δ =
Werthe von w für
φ = 0,35 und δ =
0,05
0,075
0,1
0,15
0,2
0,05
0,075
0,1
0,15
0,2
15/12
1,248
1,270
1,282
1,325
1,361
1,189
1,211
1,226
1,263
1,301
14/12
1,138
1,159
1,179
1,224
1,262
1,072
1,093
1,115
1,158
1,199
13/12
1,000
1,026
1,052
1,095
1,139
0,936
0,959
0,985
1,028
1,074
1
0,856
0,881
0,902
0,954
1,000
0,788
0,814
0,837
0,891
0,933
11/12
0,705
0,731
0,754
0,303
0,848
0,638
0,663
0,688
0,737
0,784
10/12
0,555
0,581
0,604
0,652
0,698
0,491
0,515
0,539
0,588
0,635
9/12
0,405
0,431
0,457
0,506
0,555
0,344
0,369
0,395
0,444
0,491
8/12
0,263
0,294
0,318
0,369
0,417
0,209
0,236
0,261
0,309
0,356
7/12
0,147
0,171
0,195
0,242
0,290
0,089
0,117
0,141
0,188
0,235
6/12
0,040
0,065
0,091
0,136
0,181
–
0,017
0,041
0,086
0,130
ψ
1,656
1,651
1,645
1,633
1,621
1,684
1,679
1,673
1,661
1,650
w
1,027
1,042
1,058
1,089
1,120
0,951
0,966
0,982
1,013
1,043
Tabelle V.
ψ
Werthe von w für
φ = 0,4 und δ =
Werthe von w für
φ = 0,45 und δ =
0,05
0,075
0,1
0,15
0,2
0,05
0,075
0,1
0,15
0,2
15/12
1,128
1,145
1,159
1,204
1,241
1,064
1,084
1,104
1,144
1,183
14/12
1,006
1,028
1,051
1,093
1,136
0,943
0,966
0,988
1,031
1,073
13/12
0,371
0,893
0,916
0,962
1,009
0,805
0,330
0,354
0,899
0943
1
0,720
0,748
0,772
0,825
0,867
0,659
0,684
0,708
0,756
0,803
11/12
0,573
0,598
0,623
0,671
0,720
0,512
0,536
0,561
0,609
0,657
10/12
0,426
0,451
0,475
0,524
0,573
0,366
0,391
0,416
0,464
0,512
9/12
0,234
0,310
0,333
0,385
0,427
0,231
0,252
0,276
0,333
0,363
8/12
0,151
0,180
0,205
0,252
0,250
0,100
0,125
0,150
0,197
0,244
7/12
0,033
0,066
0,089
0,135
0,181
–
0,016
0,039
0,085
0,131
6/12
–
–
–
0,039
0,082
–
–
–
–
–
ψ
1,711
1,706
1,700
1,689
1,678
1,737
1,732
1,717
1,715
1,705
w
0,875
0,890
0,907
0,937
0,568
0,801
0,816
0,860
0,863
0,894
Taf. G. S. Thallmayer: Zur Beurtheilung der Reinheit des Schnittes von
Mähemaschinen. S. 528–529
Tabelle VI.
ψ
Werthe von w für
φ = 0,5 und δ =
0,05
0,075
0,1
0,15
0,2
15/12
1,004
1,025
1,046
1,085
1,124
11/12
0,881
0,904
0,926
0,969
1,011
13/12
0,739
0,765
0,792
0,837
0,881
1
0,594
0,621
0,645
0,693
0,739
11/12
0,450
0,475
0,500
0,548
0,595
10/12
0,308
0,332
0,356
0,405
0,453
9/12
0,173
0,197
0,220
0,267
0,303
8/12
0,050
0,074
0,098
0,145
0,191
7/12
–
–
–
0,039
0,083
6/12
–
–
–
–
–
ψ
1,763
1,757
1,752
1,741
1,729
w
0,727
0,743
0,759
0,790
0,824
Um die Verwendbarkeit obiger Tabellen zu zeigen, sei z.B. 1) für
eine Getreidemähemaschine v/2 = 10cm, ψ =
7/12 (demnach h = 5cm,83) und b = 3cm,78 angenommen, weiters noch φ = 0 und δ =
0,075. Tabelle I gibt für diese Annahmen w = 0,615.
Daraus folgt nun r = 7, b₁ = 0cm,52 und z = 0. Wird der Fahrraddurchmesser mit 80cm angenommen, so ergibt sich für das
zugehörige Uebersetzungsverhältniß n = 12,5.
2) Für eine combinirte Mähemaschine sei v/2 = 5cm ,9, ψ = 11/12 (damit gleichzeitig h = 5cm,4)
sowie b = 3cm,5; ferner sei noch φ = 0,2, δ = 0,1 angenommen. Es findet sich aus Tabelle
III für w der Werth 0,904; somit ist r = 4,35, b₁ = 0,44
und z = 0cm,87.
Versieht man die Maschine mit 75cm hohen
Fahrrädern, so ergibt sich als zugehöriges Uebersetzungsverhältniß n = 19,96.
3) Für eine Grasmähemaschine sei v/2 =
4cm,5, Ψ = 15/12 (somit h = 5cm,63) und b =
3cm,75. Nimmt man φ = 0,45, δ =
0,15 an, so ergibt sich aus der Tabelle V der zugehörige Werth w = 1,144 und hiermit ist für r = 3,77, b₁ = 0,56 und z = 1cm,68 zu
nehmen. Bei einem Fahrraddurchmesser von 75cm entspricht das Uebersetzungsverhältniß n =
26,18. – Würde man in diesem Falle φ = 0,2
und δ = 0,2 annehmen, so ergäbe sich als
zugehöriger Werth von w aus Tabelle III w = 1,486, bezieh. r = 2,91,
b₁ = 0,58 und z =
0cm,58.
Es lassen sich für zwischen den Grenzen von v/2 (4,5 und 10cm) liegende
Werthe aus den Tabellen passende Werthe für ψ und
w und dadurch auch passende
Uebersetzungsverhältnisse n finden.
In den Figuren
4 und 8 stellen die mit M bezeichneten Punkte die
Mitte des Abstandes der Durchschnittspunkte der Curven I und II vor, welche zwei auf
einander folgenden Schnitten der Messerschiene entsprechen. Die Entfernung der
Punkte M von der X-Achse des ursprünglich gewählten Coordinatensystemes ist r – b und es kann
diese Differenz entweder
positiv (Fig.
4) oder negativ (Fig. 8) ausfallen. Sollen
nun die Schnitte für den Hin- und Hergang der Messerschiene unter gleichen
Bedingungen erfolgen, so müssen die Fingerkanten um diese Punkte symmetrisch
angeordnet sein. Die Entfernung zweier solcher Punkte M
ist dann auch identisch mit der Fingertheilung t. Die
Fingerdicke darf aus Festigkeitsrücksichten, und weil sich bei abnehmender
Fingerdicke der Betrag von pq vergrößert, unter
ein gewisses Maß nicht sinken (Fig. 8), aber auch nicht
allzu groß sein, weil sonst zum Aufnehmen der Halme zu wenig Raum erzielt würde;
ihre Dicke beträgt gewöhnlich zwischen 2,5 bis 3cm.
Ungarisch-Altenburg, Juni 1877.
Tafeln