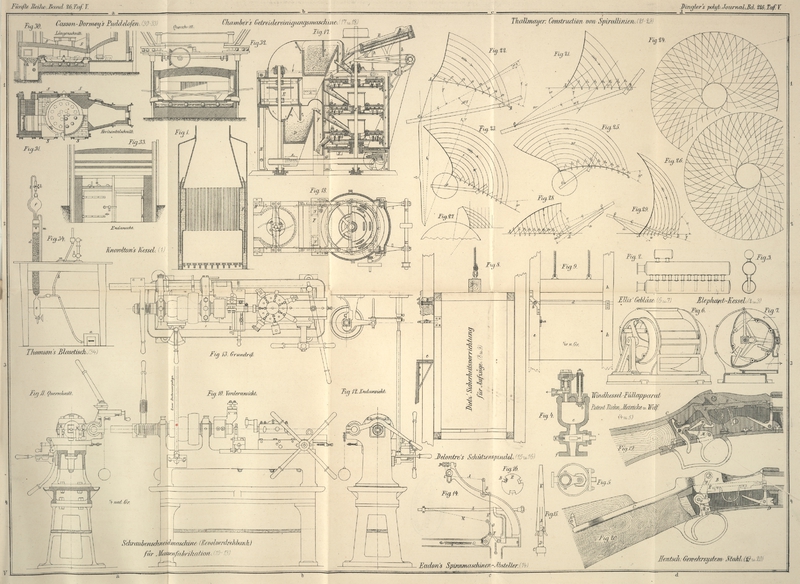
| Titel: | Annäherungsweise Construction gewisser Spirallinien; von Prof. V. Thallmayer. |
| Autor: | V. Thallmayer |
| Fundstelle: | Band 226, Jahrgang 1877, S. 157 |
| Download: | XML |
Annäherungsweise Construction
gewisser Spirallinien; von Prof. V. Thallmayer.
Mit Abbildungen auf Taf. V [c.d/1].
Thallmayer's Construction gewisser
Spirallinien.
Die Curven, nach welchen die Schneidekante der Messer einiger
Häckselschneidemaschinen, die Kanten der Mühlstein-Haufurchen
geformt werden, gehören, wie bekannt, den Spirallinien an. Wenn
auch schon für die Verzeichnung speciell der Hauschlagcurven in
den Werken über Mahlmühlen verschiedene Methoden angeführt
erscheinen, so erlaube ich mir dennoch hier eine einfache
Verzeichnungsweise für derartige Curven mitzutheilen, da sie in
vielen Fällen angewendet werden kann.
Soll die Form der Kante eines rotirenden Schneidewerkzeuges,
welches Schnitt oder Zertheilung des Materials an einer
feststehenden Kante zu vollführen hat, unter der Bedingung
construirt werden, daß der Schnitt stets unter demselben Winkel,
oder unter nach einem bestimmten Gesetze sich
ändernden Winkeln stattfinde, so verfahre man einfach, wie
folgt: Man verzeichne sich die feststehende Schnittkante AB, die in Fig. 21,
23, 28 und
29 als Gerade, in Fig. 22
und 25
hingegen als Kreisbogen angenommen wurde, und ziehe vom Punkte
A an in gleichen Entfernungen von
einander concentrische Kreise aus dem Punkte O, um welchen die schneidende Kante
rotirt. Diese Kreise schneiden die feststehende Kante in
Punkten, die in den Figuren mit 1, 2, 3... bezeichnet
erscheinen. An diese Punkte und die feststehende Kante
verzeichne man die Schnitt- oder Kreuzungswinkel α, wodurch man an den Kreisen die
Schnittpunkte s, s₁, s₂... erhält. Nun nehme man As als Anfangselement der Curve an
und füge die Stücke 1 s₁, 2
s₂, 3 s₃... successive an As an.
Das Aneinanderfügen der einzelnen die Curve bildenden Elemente
kann am Zeichenbrete, wie man leicht einsehen wird, sehr einfach
mit Zuhilfenahme von Pauspapier geschehen; auf einem Brete aber,
um etwa eine Schablone in Naturgröße anzufertigen, kann
dasselbe, wie es auch in den Figuren ersichtlich gemacht ist,
nicht minder einfach mit Hilfe zweier scharnierartig
zusammengefügten Lineale erfolgen.
Dadurch, daß man die Entfernung der concentrischen Kreise von
einander klein annimmt, und daß man etwa noch am Ursprunge der
Curve bei A, wo sie eine schärfere
Krümmung besitzt als wie am Außenende, die Kreise dichter an
einander wählt, kann man eine praktischen Zwecken genügend
entsprechende Genauigkeit erreichen.
Fig. 24 und 26 zeigen
(abgebrochen) je ein Paar Mühlsteine mit 12 Feldern, wo Haupt-
sowie Nebenfurchen denselben Zug haben, und zwar sind die
Haufurchen des Bodensteines in Figur 24
Gerade, in Figur 26
hingegen Kreisbogen. Die Haufurchen des Läufers sind so
construirt, daß die Kreuzungswinkel vom Läuferauge an gegen die
Peripherie hin continuirlich von 90° auf 30°
abnehmen und zwar in dem Maße, als die Entfernung der Punkte 1,
2, 3, 4... auf der Furche des Bodensteines vom Punkte A an zunehmen (Fig. 23
und 25). Die
Kreuzungswinkel, die in einem und demselben Kreise liegen, sind
hierbei natürlicherweise constant.
Die Gestalt der Schneide oder Zertheilungskante hängt, wie dies
auch aus den Figuren ersichtlich, von der Lage des
Drehungspunktes und von der Gestalt der feststehenden Kante ab;
sie kann entweder Convexität oder Concavität oder beides vereint
gegen die feststehende Kante kehren.
Dab im Vorstehenden besprochene, unmittelbar
aus den gestellten Anforderungen entspringende, annäherungsweise
richtige Constructionsverfahren führt übrigens auch zur Bestimmung
der Polargleichung dieser Curven. Nimmt man nämlich O als Ursprung des Coordinatensystemes
und sind die Polarcoordinaten ρ und φ, ferner
α der Kreuzungswinkel an
irgend einer Stelle, γ der
Winkel, den der Radiusvector mit der Tangente an die
feststehende Schnittkante an jener Stelle einschließt, so ist
(α + γ) der Winkel, den der Radiusvector mit der
Tangente der zu verzeichnenden Curve an jener Stelle bildet. Aus
der Analysis her ist die Richtigkeit der Gleichung dρ = ρdφ cotg (α + γ)
bekannt.
Drückt man nun γ als Function von ρ oder φ aus, so
z.B. nach Figur 21
durch sin γ : sin ω = α : ρ, oder nach Figur 22
durch b² = r² + ρ² 2rρ
cos (90 – γ), und ist das Gesetz, nach
welchem α sich verändern
soll, in Abhängigkeit zu φ
oder ρ zu bringen, so kann
durch Integration die Gleichung der Curve gefunden werden.
In dem einfachen, der Figur 21
entsprechenden Falle, wo α
constant ist, erhält man nach Integration des Ausdruckes für dφ und Bestimmung der
Constanten als Polargleichung der Curve:
Textabbildung Bd. 226, S. 158
Für ω = 0
geht (1) in die Gleichung der logarithmischen Spirale über. Für
α = 90° geht (1) über
in die Gleichung
Textabbildung Bd. 226, S. 158
und die dieser Gleichung zukommende
Curve Figur 27
kann bei der Construction von Hebedaumen verwendet werden,
umsomehr deshalb, weil die Berührungsfläche zwischen Daumen und
Ansatz des Stempels stets rechtwinklig auf die Hubrichtung
bleibt.
Für α =
90° und gleichzeitig ω
= 90° geht (1) in die Gleichung
Textabbildung Bd. 226, S. 158
der Polargleichung der gewöhnlichen
Kreisevolvente über.
Das Anführen der Gleichungen von andern
Annahmen entsprechenden Curven kann hier mit Anfügung der
Bemerkung, daß sie cyclometrische und logarithmische Ausdrücke
enthalten, umsomehr wegbleiben, als sie ihrer Complicirtheit
wegen für den praktischen Gebrauch ohne Belang sind. Ist die
feststehende Kante nach einem Kreisbogen geformt, der
gleichzeitig auch durch den Drehungspunkt der schneidenden Kante
geht, so bekommt man unter Annahme constanter Schneidewinkel als
Gleichung der schneidenden Kante eine aus zwei Gliedern
bestehende, der Gleichung 1 ähnliche Gleichung.
Ungarisch-Altenburg, Juli 1877.
Tafeln