| Titel: | Ellipsograph von Prof. V. Thallmayer in Ungarisch-Altenburg. |
| Autor: | V. Thallmayer |
| Fundstelle: | Band 227, Jahrgang 1878, S. 337 |
| Download: | XML |
Ellipsograph von Prof. V. Thallmayer in
Ungarisch-Altenburg.
Mit Abbildungen auf Tafel
21.
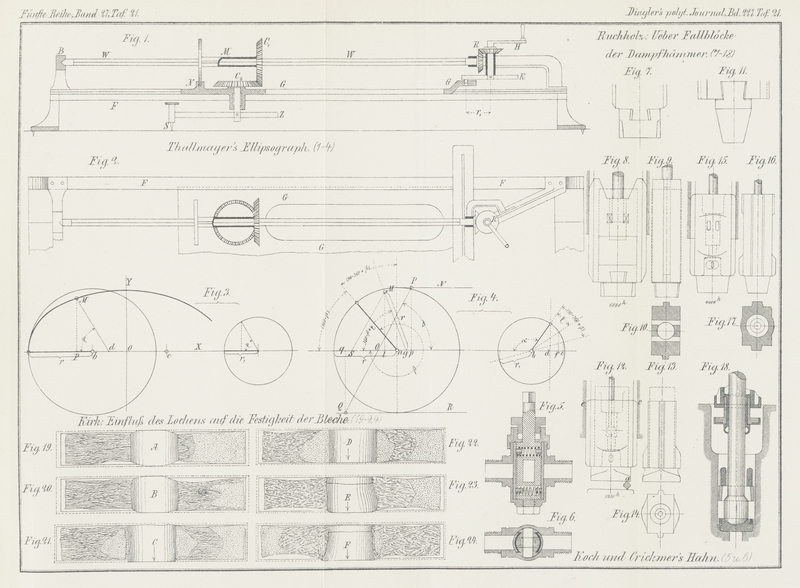
Thallmayer's Ellipsograph.
Einen Ellipsographen, welchem dieselbe Idee zu Grunde liegt wie jenem in D. p. J. * 1877 226 237
beschriebenen, erlaube ich mir nun in einer Form vorzuführen, die seine Verwendung
auch auf dem Zeichenbrete möglich macht. Er besteht aus zwei Führungsschienen F (Fig. 1 und 2 Taf. 21), zwischen
welche ein Gleitstück G eingesetzt ist. Die Bewegung
dieses Gleitstückes wird durch eine Kurbelschiene K,
die in einen Schlitz einspielt, hervorgebracht. In dem Gleitstücke befindet sich ein
verticaler Zapfen, in dessen unteres Ende eine Zirkelschiene Z Angesteckt ist und deren Umdrehung gleichzeitig mit der Bewegung des
Gleitstückes durch die Drehung der Handkurbel H
veranlasst wird.
Hierbei wird vom Stifte S der Zirkelschiene eine Ellipse
beschrieben, was weiter unten bewiesen ist.
Der Halslagerständer, welcher die Achse des horizontalen Kegelrades R und jenes Ende der wagrechten Welle W aufnimmt, auf das ein mit R gleichgrosses Kegelrad aufgesteckt wird, ist an die Führungsschienen
unbeweglich befestigt. Die Horizontalwelle W ist mit
ihrem andern Ende in den Bügel B gelagert, der
ebenfalls auf den Führungsschienen aufruht. Die Welle W
ist, mit Ausnahme jener Stellen, wo sie in Lagern läuft, von quadratischem
Querschnitte und nimmt das mit einem Muff M versehene
und lose aufgesteckte conische Rad C1 auf; dasselbe setzt das gleichgrosse conische Rad
C2 und den
verticalen Zapfen der Zirkelschiene in Bewegung. Es ist nun leicht einzusehen, dass
mit dem Umdrehen der Handkurbel H die Drehung und die
fortschreitende Bewegung der Zirkelschiene gleichzeitig eintreten müssen. Damit
während des Verschiebens des Muffes M auf der
quadratischen Welle W der richtige Eingriff der Räder
C1 und C2 aufrecht erhalten bleibt, ist das Ende des Muffes
als Scheibe geformt, die in eine am Gleitstücke befindliche Nase N einspielt.
Der Nachweis, dass die vom Stifte S beschriebene Curve
eine Ellipse ist, lässt sich leicht führen.
Vorerst sei angenommen, dass in der Anfangsstellung (Fig. 3 Taf. 21)
Zirkelschiene und Kurbelschiene in eine Richtung fallen. Während einer vollen
Umdrehung legt der verticale Zapfen der Zirkelschiene, wenn die zur Wirkung kommende
Länge der Kurbelschiene mit r1 bezeichnet wird, die geradlinige Strecke bc=2\,r_1
zurück. Nimmt man nun den Halbirungspunkt O dieser
Strecke als Ursprung eines rechtwinkligen Coordinatensystemes an, dessen
Abscissenachse parallel der Richtung der Führungsschienen liegt, so nähert sich,
nach einer aus der Anfangslage stattgehabten Umdrehung der Kurbelschiene um den
Winkel φ, der verticale Zapfen der Zirkelschiene dem
Ursprünge des Coordinatensystemes auf die Entfernung
dO=r_1\,cos\,\varphi und es ist dann, wie aus Fig. 3 leicht zu
entnehmen, MP=y=r\,sin\,\varphi und
OP=x=(r+r_1)\,cos\,\varphi. Durch Elimination der
trigonometrischen Functionen des Winkels φ ergibt sich
als Resultat die Gleichung einer Ellipse,
\frac{x^2}{(r+r_1)^2}+\frac{y^2}{r^2}=1, deren Halbmesser r und r+r_1 betragen.
Sind Kurbelschiene r1 und Zirkelschiene r
in ihrer Anfangslage unter beliebigen Richtungen zu einander gekehrt, wie in Fig. 4 Taf. 21,
so beschreibt der Stift der Zirkelschiene ebenfalls eine Ellipse, was im
Nachfolgenden erwiesen ist. Der Winkel, den die Kurbelschiene r1 mit der Richtung der
Führungsschiene einschliesst, sei α und jener, den die
Richtung der Zirkelschiene mit der der Führungsschiene einschliesst, β. Nehmen wir als Abscissenachse eines schiefwinkligen
Coordinatensystemes die Linie an, in welcher der Verticalzapfen der Zirkelschiene
hin und her geht, und als Ordinatenachse die Linie, welche jene zwei Punkte der
entstehenden Curve verbindet, die von der Abscissenachse senkrecht um die Entfernung
r abstehen. Diese Punkte werden offenbar jene sein,
bei welchen die Zirkelschiene senkrecht auf die Abscissenachse steht. Die
Zirkelschiene übergeht aus ihrer Anfangslage in diese Stellung nach Vollführung
einer Drehung um den Winkel 90-(360-\beta) und es ist dann der
Vertical zapfen der Zirkelschiene um das Stück
dc=r_1\,sin\,(\alpha+\beta)-r_1\,cos\,\alpha=ap vom Punkte
a aus auf der Abscissenachse vorgerückt. Errichtet
man nun im Punkte p eine Senkrechte auf die
Abscissenachse, bis sie die zu letzterer in der Entfernung r parallel gezogene Linie PN im Punkte P schneidet, so ist P
offenbar ein Punkt der Curve, welcher von der Abscissenachse senkrecht um die
Entfernung r absteht. Der zweite analoge Punkt der
Curve findet sich ähnlich wie der erste, wenn man von a
aus die Entfernung r_1\,cos\,\alpha+r_1\,sin\,(\alpha+\beta) bis
zum Punkte q abträgt, dort eine Senkrechte auf die
Abscissenachse errichtet und ihren Durchschnittspunkt Q
mit der zur Abscissenachse parallelen Linie QR
bestimmt.
Nehmen wir nun den Halbirungspunkt der Strecke pq als Anfangspunkt des vorhin erwähnten
schiefwinkligen Coordinatensystemes, dessen Coordinatenwinkel mit Δ bezeichnet sein möge, an, so steht nach einer Drehung
um den Winkel φ die Zirkelschiene um den Winkel
360-\beta+\varphi von der Abscissenachse ab; die Strecke, um
welche sich der Vertical zapfen der Zirkelschiene vom Anfangspunkte des
Coordinatensystemes entfernt hat, ist
Og=bf=r_1\,cos\,(\alpha+\varphi)
und M ein Punkt der Curve, dessen Ordinate
MS=y, die Abscisse OS=x. Errichtet man
dann vom Punkte M eine Senkrechte Ml auf die Abscissenachse, so ist
y\,sin\,\Delta=r\,sin\,(\beta-\varphi) und
x=y\,cos\,\Delta+r\,cos\,(\beta-\varphi)-r_1\,cos\,(\alpha+\varphi).
Behufs Elimination der trigonometrischen Functionen des Winkels φ aus diesen Gleichungen hat man aus der ersten
sin\,(\beta-\varphi)=\frac{y\,sin\,\Delta}{r} und daraus:
sin\,\varphi=-\frac{y\,cos\,\beta\,sin\,\Delta}{r}+sin\,\beta\sqrt{1-\frac{y^2\,sin^2\Delta}{r^2}}
und
cos\,\varphi=\frac{y\,sin\,\beta\,sin\,\Delta}{r}+cos\,\beta\sqrt{1-\frac{y^2\,sin^2\Delta}{r^2}}.
Löst man in der zweiten Gleichung
cos\,(\alpha+\varphi) in seine zwei Glieder auf und setzt
darin die eben gefundenen Werthe von sin φ und cos φ, sowie jenen von
cos\,(\beta-\varphi) ein, so erhält man die Gleichung x=y\,cos\,\Delta-\frac{r_1\,y\,sin\,(\alpha+\beta)\,sin\,\Delta}{r}+\sqrt{1-\frac{y^2\,sin^2\Delta}{r^2}}\,[r+r_1\,cos\,(\alpha+\beta)]x=y\,cos\,\Delta-\frac{r_1\,y\,sin\,(\alpha+\beta)\,sin\,\Delta}{r}+\sqrt{1-\frac{y^2\,sin^2\Delta}{r^2}}\,[r+r_1\,cos\,(\alpha-\beta)]. Nun ist sin\,\Delta=\frac{Pp}{OP},\
cos\,\Delta=\frac{Op}{OP} und da
bc=op=r_1\,sin\,(\alpha+\beta) ist, auch:
sin\,\Delta=\frac{r}{\sqrt{r^2+{r_1}^2\,sin^2(\alpha+\beta)}} und
cos\,\Delta=\frac{r_1\,sin\,(\alpha+\beta)}{\sqrt{r^2+{r_1}^2\,sin^2(\alpha+\beta)}}.
Diese Werthe in obige Gleichung eingeführt, geben ihr nach
einfacher Reduction die Form: \frac{x^2}{[r+r_1\,cos\,(\alpha+\beta)]^2}+\frac{y^2}{r^2+{r_1}^2\,sin^2\,(\alpha+\beta)}=1,\frac{x^2}{[r+r_1\,cos\,(\alpha-\beta)]^2}+\frac{y^2}{r^2+{r_1}^2\,sin^2\,(\alpha+\beta)}=1, die Gleichung einer Ellipse, bezogen auf die conjugirten Halbmesser r+r_1\,cos\,(\alpha+\beta)r+r_1\,cos\,(\alpha-\beta) und \sqrt{r^2+{r_1}^2\,sin^2\,(\alpha+\beta)}.
Schliesslich noch die Bemerkung, dass der Stift S auch
dann noch Ellipsen beschreibt, wenn die als ruhend angenommene Unterlagsfläche durch
die Kreis- oder Ellipsendrehung einer Kurbelwarze in geradlinig schwingende Bewegung
versetzt würde.
Tafeln