| Titel: | Hygrometer von W. Klinkerfues in Göttingen. |
| Fundstelle: | Band 234, Jahrgang 1879, S. 208 |
| Download: | XML |
Hygrometer von W. Klinkerfues in
Göttingen.
Mit Abbildungen auf Tafel 19.
Kinkerfues' Hygrometer.
Zur weiteren Erläuterung des bereits (1877 226 100) kurz
besprochenen Haarhygrometers von W. Klinkerfues in
Göttingen möge nach der Patentschrift (* D. R. P. Nr. 3366 vom 18. November 1877)
noch folgende Angaben nachgetragen werden. (Vgl. auch S. 46 d. Bd.)
Gay-Lussac hat für eine mittlere Temperatur bestimmt,
welcher relativen Feuchtigkeit der Luft die Grade des Saussure'schen Hygrometers
entsprechen; er gibt folgende Tabelle:
0°
=
0,00
relative
Feuchtigkeit
10
=
4,57
„
„
20
=
9,45
„
„
30
=
14,78
„
„
40
=
20,78
„
„
50
=
27,79
„
„
60
=
36,28
„
„
70
=
47,19
„
„
80
=
61,22
„
„
90
=
79,09
„
„
100
=
100,00
„
„
Da die Zahl der Grade des Saussure'schen Haarhygrometers der Verlängerung
proportional ist, welche das Haar durch Feuchtigkeit erlitten hat, so sieht man, wie
der betreffende Ausdehnungscoefficient sich mit dem Procentsatz relativer
Feuchtigkeit ändert, und nun kann man aus obigen Zahlen eine für das Folgende
wichtige Eigenschaft jenes Coefficienten ableiten. Die der Ausdehnung proportionale
Anzahl der Grade, welche mit y bezeichnet werden mag,
läſst sich nämlich durch folgende Formel als Function des Feuchtigkeitsprocentes p darstellen:
y = 126,91 – 47,901 cotg (0,400°p +
20,68°),
woraus sich dann gleich ergibt, daſs der
Ausdehnungscoefficient dem Quadrate des Ausdruckes sin
(0,400° p + 20,68°) umgekehrt proportional ist. Es
scheint sich die Voraussetzung zu bewahrheiten, daſs diese Eigenschaft immer für
eine ganze Art von Haaren giltig bleibt, nur daſs die Zahlencoefficienten von Art zu
Art wechseln. Daſs der Ausdehnungscoefficient durch Feuchtigkeit sehr nahe gerade in
der angegebenen Weise veränderlich ist, hat für das neue Hygrometer dieselbe
Bedeutung, welche die ebenfalls nur sehr angenähert stattfindende Unveränderlichkeit
des Ausdehnungscoefficienten der meisten Körper durch Wärme für die Thermometer
besitzt. Die obige Formel läſst höchstens einen Fehler übrig, welcher an einer wenig
gebrauchten Stelle der Scale 1,61 Procent der Feuchtigkeit erreicht und der selbst
für die meisten wissenschaftlichen Untersuchungen nicht sehr in Betracht kommt.
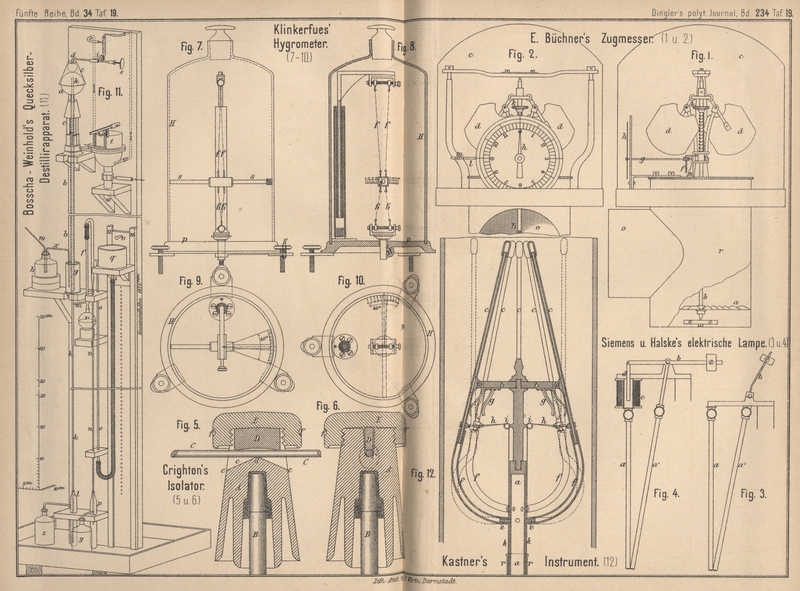
Man denke nun nach Fig. 7 der
beigegebenen Zeichnung auf Taf. 19 ein Stäbchen ss an zwei hygroskopischen Fäden f bifilar
aufgehängt, gleichzeitig aber durch zwei andere solcher Fäden f1 verhindert, ganz der Torsion der ersten Fäden
nachzugeben. Die Ruhelagen, nach welchen die sich entgegenwirkenden Torsionen
streben, sollen senkrecht zu einander sein, daſs also, wenn z der Torsionswinkel der unteren Torsion ist, der der oberen durch 90° –
z ausgedrückt wird. Die von letzterer ausgeübte
Directionskraft läſst sich demnach ausdrücken durch c1 sin z, die der ersteren durch c cos x, wenn c1 und c die
Maximalwerthe dieser Kräfte bezeichnen. Soll sich das Stäbchen unter dem Einflüsse
beider Kräfte im Gleichgewichte befinden, so
muſs c_1\,sin\,z-c\,cos\,z=0, d.h. es muſs
cotg\,z=\frac{c_1}{c} erfüllt sein.
Erleidet nun die Gröſse \frac{c_1}{c} aus
irgend welcher Ursache, z.B. durch die Einwirkung von Feuchtigkeit auf die
hygroskopischen Fäden eine kleine Variation
\delta\,\frac{c_1}{c}, geht also in
\frac{c_1}{c}+\delta\,\frac{c_1}{c} über, so geht auch
entsprechend der Torsionswinkel z in z+\delta
z über, und man hat cotg\,(z+\delta
z)=\frac{c_1}{c}+\delta\,\frac{c_1}{c} oder mit Rücksicht auf die
Kleinheit von δz, die ihre höheren Potenzen zu
vernachlässigen erlaubt, \delta
z=-\,sin\,z_2\,\delta\,\frac{c_1}{c}.
Die Gröſsen c1 und c hängen u.a.
nach den Torsionsgesetzen von der Länge und von dem Abstande von je zwei Fäden eines
Paares ab. Die Variation oder das Increment \delta\,\frac{c_1}{c}
ist also hier als eine Function der Ausdehnungen anzusehen, welche die Fäden durch
Feuchtigkeit erleiden, und zwar mit Rücksicht auf die Kleinheit dieser Gröſsen, als
eine linäre Function. Man kann daher nach obigem setzen:
\delta\,\frac{c_1}{c}=\frac{\gamma \delta
p}{sin\,(0,400^{\circ}\,p+20,68^{\circ})^2},
wobei y eine Constante,
δp das Increment der relativen Feuchtigkeit
bedeutet, durch welches die Störung des Gleichgewichtes der beiden Torsionen
veranlaſst wird. Substituirt man den oben gefundenen Ausdruck von
\delta\,\frac{c_1}{c} in der Gleichung für δz, so wird:
\delta z=\sqrt{\frac{sin\,z^2\gamma \delta
p}{sin\,(0,400^{\circ}\,p+20,68^{\circ})^2}}, . . . . . . . (1)
wobei sich die Coefficienten auf Menschenhaare
beziehen.
Durch Abänderungen in der Spannung, in der Länge oder in der Weite
der Fädenpaare läſst sich für die Constante y der Werth
– 0,400 herstellen. Gesetzt, dies sei geschehen, auſserdem aber noch für irgend eine
Stellung in der Gleichgewichtslage, welcher der Torsionswinkel z0 und die relative
Feuchtigkeit p0
entspricht, durch Aenderungen im Verhältniſs beider Torsionen erreicht, daſs:
z_0=0,400^{\circ}\,p+20,68^{\circ} . .
. . . . . . . . . (2)
ist, so wird überall, d.h. die ganze Scale der
relativen Feuchtigkeit hindurch z = 0,400° p + 20,68°; denn es wird zufolge der Gleichung (1) für
p = p0 die Gröſse
δz= 0,400 δp, folglich ist die Bedingung (2) auch für die Nachbarwerthe von z0 und p0, nämlich für z0 + δz und p0 + δp erfüllt
und deshalb der gemachte Schluſs durch die ganze Scale zu wiederholen. Umgekehrt ist
auch die Erfüllung der Bedingung (2) für zwei z.B. für die äuſseren Punkte der
Feuchtigkeitsscale p = 0 und p = 100 ein Zeichen, daſs y = 0,400 gemacht
worden ist. Hieraus folgt, daſs man eine gleichwertige Scale haben wird, wenn man
dafür sorgt, daſs in getrockneter Luft z = 20,68°, in
gesättigter gleich 60,68° wird, und daſs unmittelbar der Procentsatz relativer
Feuchtigkeit angegeben wird, wenn man das Stäbchen auf einem in 100 gleiche Theile
getheilten Gradbogen von 40° spielen läſst, dessen Nullpunkt z = 20,68° entspricht, oder, wenn man das Stäbchen senkrecht zu der erst
angegebenen Lage durch
das Schiffchen mit den Aufhängepunkten steckt: z =
45,00° – 20,68° = 20,00° + 4,32°.
Die Möglichkeit der eben angegebenen Regulirung erhellt
theoretisch aus der Betrachtung, daſs die Bedingung des Zusammenhaltens von p = 0 mit z = 20,68°
dadurch zu erfüllen ist, daſs man das Verhältniſs beider Torsionen ändert, die
anderen aber des Zusammenfallens von p = 100 mit z = 60,68°, wenn die Empfindlichkeit, d.h. die Summe
bezieh. die Differenz beider Torsionen, geändert wird, und zwar durch solche
gleichzeitige Correction beider Torsionen, daſs das Verhältniſs für die andere
Stellung p = 0 dasselbe bleibt.
Die Empfindlichkeit des in Fig. 7 bis
10 Taf. 19 dargestellten Apparates überhaupt und die Gröſse der Torsion
wird am bequemsten dadurch geändert, daſs man die Fäden an ihrem einen Ende einander
nähert, oder von einander entfernt. Die bifilare Torsion ist, wenn die Fäden nicht
parallel sind, sondern mit der Aufhänge- oder Befestigungsbasis ein Trapez bilden,
dem Product aus den beiden parallelen Seiten des Trapezes proportional. Wird die
Verstellung durch Schrauben ausgeführt, so ist die Aenderung des Werthes der
Torsionscoëfficienten der Drehung der Schraube proportional.
Bei dem Justiren des Instrumentes ist es auch nöthig, die Spannung der Fäden ganz
allmälig mittels einer Schraube, welche das Befestigungsstück der oberen Fäden
bequemer nach der unteren in verticaler Richtung verschiebt, verändern zu können.
Mittels derselben Schraube können die Fäden auch ganz auſser Spannung gesetzt
werden, um das Stäbchen zu arretiren. In diesem Zustande kann das Instrument
versendet werden. Um es wieder zu justiren, braucht man nur auf die Platte p des Instrumentes, welche mittels dreier Fuſsschrauben
horizontal gestellt worden, ein Tellerchen mit Chlorcalcium zu bringen, dann mit der
Glasglocke H zu bedecken und mittels der Schraube S die Spannung der Fäden so weit zu vergröſsern, daſs
mit dem allmäligen Austrocknen der Luft in der Glocke der Zeiger das Stäbchen ss auf den Nullpunkt der Theilung geführt wird.
Mit derselben Schärfe aber kann man dieselbe Spannung wieder herstellen, wenn man
die Schwingungsdauer des Stäbchens beobachtet, was selbst mit einer gewöhnlichen
Secunden zeigenden Uhr leicht auszuführen ist, Zu diesem Zwecke bemerkt der
Mechaniker, wie viel Schwingungen in einer oder mehreren Minuten in vollkommen
ausgetrockneter Luft gemacht werden müssen.
Bei dem Aufstellen des Apparates an einem anderen Orte wird Chlorcalcium auf die
Platte p gebracht, eine Glocke H übergestülpt und mittels der Schraube S die
Spannung der Fäden so lange berichtigt, bis nach vollständiger Austrocknung der Luft
in der Glocke der Zeiger auf Null oder noch besser das Stäbchen die diesem Punkte
entsprechende Schwingungszahl zeigt.
Tafeln