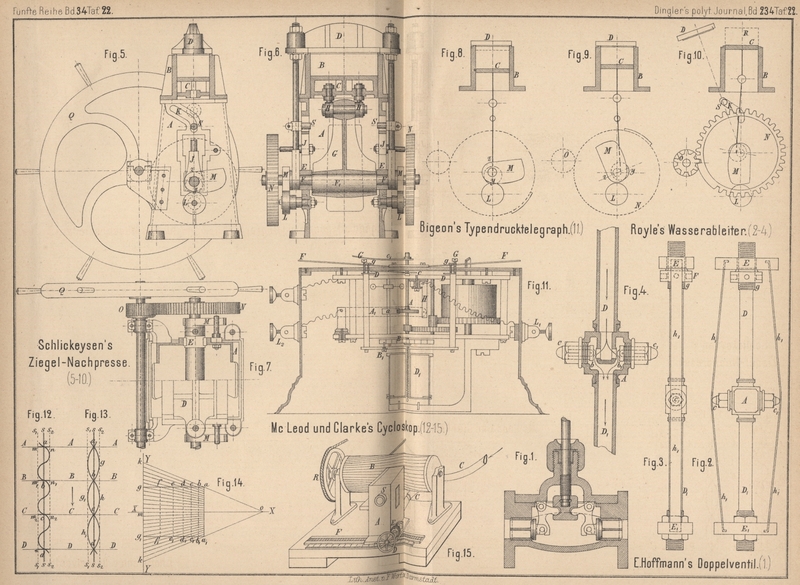
| Titel: | Optischer Tourenzähler (Cycloskop) von McLeod und Clarke. |
| Autor: | A. P. |
| Fundstelle: | Band 234, Jahrgang 1879, S. 295 |
| Download: | XML |
Optischer Tourenzähler (Cycloskop) von McLeod und Clarke.
Mit Abbildungen auf Tafel 22.
McLeod und Clarke's optischer Tourenzähler.
Die Professoren McLeod und Clarke vom „Royal Indian Engineering College“
haben unter der Bezeichnung „Cycloskop“ einen höchst sinnreichen Apparat construirt, mit dessen Hilfe die
augenblickliche Tourenzahl einer Achse zu jeder Beobachtungszeit genau bestimmt
werden kann. Ihre Methode beruht auf jener bekannten physiologischen Erscheinung,
der auch das Phenakistoskop oder die stroboskopische Scheibe ihre optische Wirkung
verdankt, nämlich auf der Dauer des Lichteindruckes im Auge.
Man denke sich auf der hellen Mantelfläche eines horizontalen
Cylinders, parallel zur Achse, ein System dunkler gerader Linien A, B, C... (Fig. 12 und
13 Taf. 22) in gleichen Abständen vertheilt. Vor dem Cylinder befinde
sich ein verticales Metallplättchen mit einem feinen verticalen Spalt s. Der Beobachter wird alsdann, so lange das System in
Ruhe ist, durch den Spalt aber nur eine Reihe gleich weit abstehender dunkler Punkte
a, b, c... erblicken. Befindet sich aber der Spalt
in einer zwischen den Grenzlagen s1 und s2 parallel zur Cylinderachse rasch hin und
her schwingenden Bewegung, so wird das Auge, vermöge der Dauer des Lichteindruckes
auf der Netzhaut, statt jener Punkte eben so viele gerade Striche mn, m1n1, m2n2... wahrnehmen.
Angenommen nun, der Cylinder drehe sich zugleich um seine Achse
und seine Geschwindigkeit sei so regulirt, daſs die von den Parallellinien A, B, C... (Fig. 12)
während einer vollständigen Schwingung des Spaltes zurückgelegte Strecke ihren
Abständen ab, bc... genau gleich sei, so wird man
durch den Spalt statt der Striche mn, m1n1... die
unbewegliche Wellenlinie (Sinuscurve) Fig. 12
erblicken. Die geringste Geschwindigkeitsänderung des Cylinders wird sich aber
augenblicklich dadurch bemerklich machen, daſs die Wellenlinie im Augenblicke der
Geschwindigkeitsvermehrung eine im Sinne der Drehung fortschreitende, bei einer
Verminderung eine rückgängige Bewegung annimmt. Bei der doppelten
Umdrehungsgeschwindigkeit des Cylinders wird der Punkt a die unbewegliche Curve agbg1c (Fig. 13)
und gleichzeitig der Punkt b die unbewegliche Curve bhch1d
hervorrufen; es muſs also im Auge der Eindruck zweier entgegengesetzter, in den
Knotenpunkten a, b, c... sich schneidender Wellenlinien
entstehen.
Bei gegebener Schwingungszahl des Plättchens ist demnach das
Auftreten beider unbeweglichen Wellengebilde Fig. 12 und
Fig. 13 das charakteristische Kennzeichen zweier ganz bestimmter
Umdrehungsgeschwindigkeiten des Cylinders. Wir wollen beispielshalber annehmen,
letzterer enthalte 24 gleich weit abstehende Parallellinien (in der Ausführung wählt
man eine weit gröſsere Anzahl) und das Plättchen mit dem Spalt mache 60 Schwingungen
in 1 Secunde, also 1 Schwingung in 1/60 Secunde. Würde sich nun hinter dem Spalt die
einfache Curve Fig. 12,
deren Wellenlänge dem Abstande ab gleich ist, als
unbewegliches Gebilde zeigen, so wäre daraus der Schluſs zu ziehen, daſs 1/24 Umdrehung auf
1/60 Secunde
oder 150 Touren auf 1 Minute kämen. Erschiene aber die Doppelcurve Fig. 13 von
der doppelten Wellenlänge ac, so wäre dies ein
Zeichen, daſs 1/12
Touren in 1 Secunde oder 300 Umdrehungen in 1 Minute erfolgen würden. Die Erfinder bedienen sich
als normaler Basis zur Ermittelung der Tourenzahl des am leichtesten erkennbaren
Gebildes Fig.
13.
Wir haben bisher, der Einfachheit wegen, die Linien A, B... als parallel angenommen. Unter dieser Annahme
würde es aber nur eine einzige Geschwindigkeit geben, welche durch das Auftreten des
zu Grund gelegten Gebildes Fig. 13
bestimmt werden könnte. Um nun im Stande zu sein, mit einer und derselben
Schwingungszahl des Spaltes jede beliebige Umdrehungsgeschwindigkeit des Cylinders
innerhalb gegebener Grenzen zu messen, bringen die Erfinder folgende geometrische
Construction in Anwendung. Man zeichnet auf ein Blatt Papier zwei rechtwinklig sich
schneidende Gerade X, Y (Fig. 14)
und construirt über X als Mittellinie ein Rechteck,
dessen Seite ag der Länge und dessen Seite aa1 dem Umfange des als
Hauptorgan des Tourenzählers wirkenden Cylinders gleich ist. Die Seite gg1 wird in eine gerade
Anzahl – wir wollen annehmen 12 – gleicher Theile getheilt und die Theilung über g und g1 hinaus gleich weit fortgesetzt, bis das
Verhältniſs mg : mk
dem Verhältnisse der beiden äuſsersten Geschwindigkeiten des Cylinders z.B. 1 : 2
gleich ist. Die von den Endpunkten k und k1 durch die Ecken a und a1 gezogenen Geraden schneiden sich in o. Zieht man nun aus o
nach sämmtlichen Theilungspunkten von kk1 gerade Linien, so schneiden diese die
beiden Rechteckseiten ag und a1g1 in den Punkten b bis f und b1 bis f1. Denkt man sich ferner sämmtliche
homologen Durchschnitte paarweise durch gerade Linien verbunden, so erhält man ein
System von Parallellinien aa1, bb1, cc1, dd1, ee1, ff1, welche durch die schrägen Linien bezieh.
in 24, 22, 20, 18, 16 und 14 gleiche Theile getheilt werden. Schneidet man das
Rechteck aus und legt es dergestalt um den Cylinder, daſs die Punkte a bis f mit den Punkten
a1 bis f1 zusammenfallen, so
verwandeln sich die Linien aa1, bb1... in Parallelkreise,
welche durch die schrägen Linien in beziehungsweise 24, 22, 20... gleiche Theile
getheilt sind. Denkt man sich endlich je zwischen zweien dieser Parallellkreise, und
zwar in der Mitte, noch einen Parallelkreis eingeschaltet, so werden die
eingeschalteten Kreise, wie leicht nachzuweisen, der Reihe nach in 23, 21, 19, 17,
15, 13 gleiche Theile getheilt.
Angenommen nun, es erscheine hinter dem Spalt, wenn er dem Kreise
aa1 gegenüber mit
der Geschwindigkeit von 60 Schwingungen in 1 Secunde schwingt, das feststehende
Wellengebilde Fig. 13, so
deutet dieses, wie oben gezeigt wurde, auf eine Geschwindigkeit von 300 Touren in 1
Minute. Müſste man aber, um die nämliche Figur zum Vorschein zu bringen, den Spalt
bis zum Parallelkreis ee1 verschieben, welcher durch die schrägen Linien in 16 gleiche Theile
getheilt wird, so würde die Geschwindigkeit ⅛ Umdrehung in 1/60 Secunden oder
450 Touren in 1 Minute betragen. Auf diese Weise läſst sich aus dem Auftreten der
Figur an der einen oder der anderen Stelle des Cylinders die Tourenzahl bei jeder
beliebigen Geschwindigkeit innerhalb der gegebenen Grenzen berechnen.
Dies ist das Princip, auf welches sich der in Rede stehende
Tourenzähler, Cycloskop genannt, gründet.
Fig.
15 Taf. 22 stellt das Instrument in einer perspectivischen Skizze dar. Der
mit der Papierfläche aa1g1g (Fig. 14)
überzogene Cylinder B steht durch eine Schnurscheibe
R mit der Maschine in Verbindung, deren
Umdrehungszahl gemessen werden soll. A ist ein parallel
zur Cylinderachse verschiebbarer Kasten, welcher eine auf 60 Schwingungen in der
Secunde regulirte elastische Platte um schlieſst, woran ein Zinkplättchen befestigt
ist. Letzteres besitzt einen schmalen verticalen Spalt, nicht breiter als die Dicke
der auf dem Cylindermantel gezogenen Linien. Die Verschiebung des Kastens A geschieht mit Hilfe des Handrädchens D, an dessen Achse ein kleines Zahnrad E sitzt, welches in eine an das Bodenbret des Apparates
befestigte Zahnstange
F greift. Zur Betrachtung der Curven dient ein
Ocular S mit Vergröſserungslinse. Die elastische Platte
wird, ähnlich wie bei Zungenpfeifen, mittels eines durch das biegsame Windrohr C eingeblasenen Luftstromes in Schwingung gesetzt. Beim
Gebrauch des Instrumentes sieht man durch das Ocular und bewirkt zugleich durch
Drehung des Rades D die erwähnte Längsbewegung des
Kastens, bis die unbewegliche Normalfigur erscheint, worauf mit Hilfe eines am Fuſse
des Kastens angebrachten Zeigers die Umdrehungszahl auf einer graduirten Scale
unmittelbar abgelesen werden kann. Prof. McLeod hat das
Instrument neuerdings noch dahin verbessert, daſs der Beobachter die Umdrehungszahl
des Cylinders ablesen kann, ohne das Auge vom Ocular zu entfernen.
Das Cycloskop zeigt die geringste Geschwindigkeitsänderung an und lehrt, daſs die
Umdrehungsgeschwindigkeit der vollkommensten Maschinen, sie mögen noch so sorgfältig
regulirt sein, beständigen Schwankungen unterworfen ist. (Nach dem Engineer, 1879 Bd. 48 S. 225.)
A.
P.
Tafeln