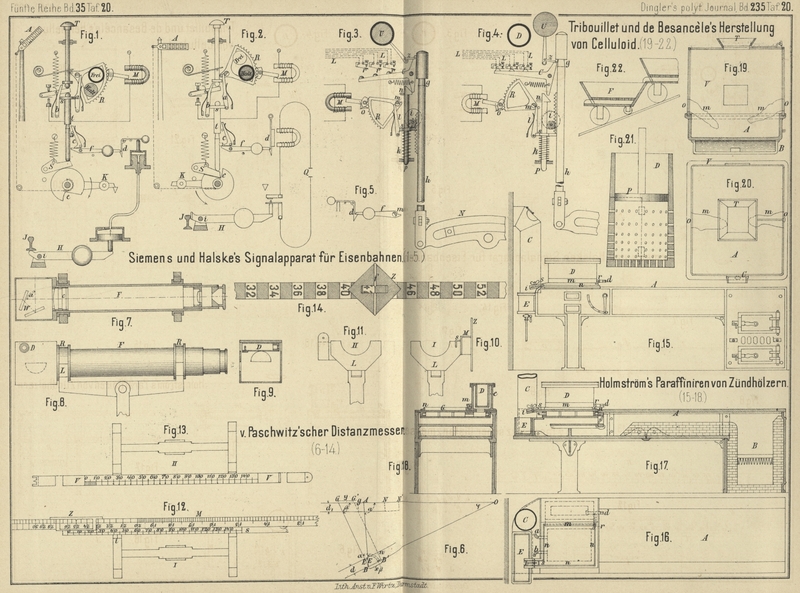
| Titel: | Der v. Paschwitz'sche Distanzmesser; von Prof. Fr. Lorber. |
| Autor: | Fr. Lorber |
| Fundstelle: | Band 235, Jahrgang 1880, S. 199 |
| Download: | XML |
Der v. Paschwitz'sche Distanzmesser; von Prof. Fr. Lorber.
Mit Abbildungen auf Tafel 20.
Lorber, über den v. Paschwitz'schen Distanzmesser.
In diesem Journal (* 1871 202 235) ist bereits eine Beschreibung des in Rede
stehenden Instrumentes enthalten; seit dieser Zeit wurde aber der Distanzmesser
mehrfach abgeändert und unter Nr. 28 vom 3. Juli 1877 ab für das deutsche Reich
patentirt. Es erscheint demnach angezeigt, auf denselben zurückzukommen und die
Beschreibung und Anwendung durch die einfache Theorie und durch Angaben über die
Genauigkeit auf Grund von durchgeführten Untersuchungen, welche Verfasser an anderer
StelleCarl's Repertorium für
Experimentalphysik u. Instrumentenkunde, 1879 S. 687.
ausführlicher besprach, zu ergänzen, zumal bis nun weder die Anwendung der
theoretischen Beziehungen der in Frage kommenden Gröſsen auf die Einrichtung des
Instrumentes, noch die zu erreichende Genauigkeit Gegenstand einer Veröffentlichung
seitens der Erfinder waren, da sich diese lediglich auf die Erklärung und Anwendung
des Instrumentes und auf allgemeine, durch keine Daten begründete Bemerkungen über
den Fehler desselben beschränkten.
Zur Messung der Entfernung eines Objectes mit dem Paschwitz'schen Distanzmesser ist die Aufstellung in zwei Punkten, welche
eine bekannte Entfernung von einander haben, und die Absteckung eines constanten
Winkels α in jedem der beiden Punkte nöthig. Wenn auch
das Princip der Distanzmessung mittels Absteckung von constanten Winkeln keineswegs
neu ist, so ist doch die Verwendung desselben bei dem vorliegenden Distanzmesser und
dessen Einrichtung, welche die unmittelbare Ablesung der Entfernung ohne irgend
welche Rechnung gestattet, ganz eigenartig, wie aus nachstehender Erörterung leicht
zu ersehen ist.
Ist etwa (Fig. 6 Taf.
20) die Entfernung AO=D zu bestimmen, und denkt man sich von A aus den constanten Winkel α, welcher nahe an 90° ist, abgesteckt und in der Richtung AB die horizontale Distanz AB=C
aufgetragen, dann aus dem Endpunkte B nach Einstellung
auf O wieder den Winkel α
abgesteckt und den Schnittpunkt G auf einem in der
Verticalebene AO zur Visirlinie AO parallel liegenden getheilten Stab markirt, so gibt der Abstand
AG=a einen Anhaltspunkt zur Ermittlung von D, denn aus den beiden Dreiecken ABO und GBO folgt:
a=b\,\frac{sin\,(\alpha-\beta)}{sin\,\beta} und
D=b\,\frac{sin\,\beta}{sin\,(\alpha+\beta)}=b\,\frac{sin\,\beta}{sin\,\varphi}.
Wäre α bekannt, so lieſse sich aus
beiden Gleichungen β ausscheiden und die zu bestimmende
schiefe Entfernung D durch a,
b und α ausdrücken; da aber α, obwohl constant, doch nicht bekannt ist und da
ferner, selbst wenn die Gröſse von α bekannt wäre, eine
Rechnung ausgeführt werden müſste, so muſs man suchen, sich von diesem Winkel
unabhängig zu machen.
Sind für eine zweite Entfernung D1 die entsprechenden Gröſsen α1, β1, so ist:
a_1=b\,\frac{sin\,(\alpha-\beta_1)}{sin\,\beta_1} und
D_1=b\,\frac{sin\,\beta_1}{sin\,(\alpha+\beta_1)}=b\,\frac{sin\,\beta_1}{sin\,\varphi_1},
und leicht findet man, daſs:
a-a_1=(D_1-D)\,\frac{b^2}{DD_1},
d.h. daſs die
Unterschiede der Stababschnitte von dem constanten Winkel α unabhängig sind und daſs somit eine etwaige Aenderung von α keinen Einfluſs auf die Unterschiede
a-a_1 haben kann. Da der Stab verschiebbar sein muſs, wie
später gezeigt wird, der Nullpunkt der Theilung aber, um verschieden bezeichnete a zu umgehen, nicht im Scheitel des Winkels α ist, sondern etwa in N,
so sind die Ablesungen am Stabe m und m1, deren Unterschied
nur dann gleich a-a_1 ist, wenn a=m-c und
a_1=m_1-c ist, d.h. wenn der Stab stets so eingelegt wird,
daſs ein bestimmter Punkt desselben mit einem fest bleibenden – von der Stab
Verschiebung unabhängigen – Index zusammenfällt.
Die Absteckung des constanten Winkels im zweiten Standpunkte von
B aus muſs vermieden werden, weil dies die
Aufstellung des Scheitels über B verlangen und daher
Zeitaufwand verursachen würde; der Winkel wird von B'
aus abgesteckt und trifft die Visur jetzt den Stab in G'; man müſste also, um nicht zu wenig abzulesen, den Stab um y verschieben, wodurch die Ablesung
N'G'=NG würde.
Um die Gröſse dieser Verschiebung zu bestimmen, kann man an einem
seitlich liegenden Stäbchen im Standpunkte II den Ort des Schnittpunktes E der Visur AB, d. i. n E ablesen; da y genau
genug gleich n E' ist, weil der Winkel φ für die kleinste zu messende Entfernung von 800m erst den Werth 1°48' erreicht, und da EE' hinreichend genau gleich
\frac{bd}{D} ist, so ergibt sich
y=n\,E+\frac{bd}{D}. Nachdem sich
\frac{bd}{D} aber, als von D
abhängig, nicht ermitteln läſst, so kann die Verschiebung blos um das abgelesene
Stück n E vorgenommen werden, so daſs also die Ablesung
auf dem Meſsstabe nicht m, sondern um
\frac{bd}{D} weniger als m
beträgt.
Berücksichtigt man weiter, daſs der Stab AN nicht in der Verticalebene AO, sondern nur
seitlich angebracht werden kann, so ersieht man, daſs die Stabablesung auch noch um
g\,G'=\frac{bd_1}{D} zu klein ausfällt, so daſs also
schlieſslich der mit Rücksicht auf diese Umstände wirklich abgelesene Stababschnitt
wird:
für die Entfernung D . . .
. .
M=m-\frac{bd}{D}-\frac{bd_1}{D}=a+c-\frac{bd}{D}-\frac{bd_1}{D},
für die Entfernung D1. . . .
.M_1=m_1-\frac{bd}{D_1}-\frac{bd_1}{D_1}=a_1+c-\frac{bd}{D_1}-\frac{bd_1}{D_1}.
Weiters ergibt sich:
M-M_1=b^2\left(\frac{1}{D}-\frac{1}{D_1}\right)-bd\,\left(\frac{1}{D}-\frac{1}{D_1}\right)-bd_1\left(\frac{1}{D}-\frac{1}{D_1}\right)=(b^2-bd-bd_1)\left(\frac{1}{D}-\frac{1}{D_1}\right)
und, wenn man d=d_1 setzt, auch
M-M_1=(b^2-2\,bd)\,\left(\frac{1}{D}-\frac{1}{D_1}\right) und
schlieſslich:
M=M_1+(b^2-2\,bd)\,\left(\frac{1}{D}-\frac{1}{D_1}\right).
Wird als gröſste zu messende Entfernung
D_1=10000^m angenommen und der dieser Entfernung
entsprechende Stababschnitt M_1=0 gesetzt, so wird
M=\frac{b^2-2\,bd}{D}-\frac{b^2-2\,bd}{10000} oder mit
Rücksicht auf die Werthe von b\ (=25^m) und d\
(=33^{mm}) auch:
M=\frac{623,35}{D}-0,062335,M und D in Meter
verstanden.
Die Entfernung selbst folgt hieraus:
D=\frac{623,35}{M+0,062335}, wobei aber zu berücksichtigen
ist, daſs der Stab so eingelegt werden muſs, daſs für die Entfernung
D=10000^m der Abschnitt M
wirklich gleich Null wird, d.h. daſs das Instrument justirt ist. Anstatt die Gröſsen D für die jeweiligen Abschnitte zu rechnen, kann der
Stab, welcher von v. Paschwitz Meſsstab genannt wird,
gleich so beziffert werden, daſs unmittelbar die Entfernung abgelesen wird; denn es
ist für:
m
mm
m
mm
m
mm
D =
800
M =
716,85
D =
4000
M =
93,50
D =
8000
M =
15,58
1000
561,02
5000
62,34
9000
6,93
2000
249,34
6000
41,56
10000
0,00.
3000
145,44
7000
26,72
Die Bestandtheile des in Fig. 7 bis
14 Taf. 20 dargestellten Distanzmessers sind: Das Fernrohr F (Fig. 7 bis
9) mit dem Winkelspiegel W, welcher die
Lichtstrahlen um den Winkel α ablenkt und dessen
Gehäuse mit dem Diopter D versehen ist. – Zwei
Dreifuſsstative I und II
(Fig. 10 und 11), welche
die Lager L zum Einlegen des Fernrohres tragen. – Der
Meſsstab M (Fig. 12),
der auf seiner oberen Seite die Distanzscale für die Entfernungen von 800 bis
10000m enthält und seitlich mit einer groben
Theilung zum unmittelbaren Ablesen mit dem Fernrohre aus 25m Entfernung versehen ist und bei Vornahme einer
Messung mittels der mit ihm fest verbundenen Messingschiene s in das Lager L des Statives I eingelegt und verschoben werden kann. – Die
Compensationsvorrichtung (Fig. 13),
welche aus dem mit einem Diopter versehenen und am Stativ II befestigten Visirstabe V und der
Messingschiene s besteht; V und s haben gleiche Theilung und im selben
Sinne (nach rückwärts) laufende Bezifferung und überdies hat V, ähnlich wie der Meſsstab, eine grobe Theilung. – Das Zielschildchen Z (Fig. 14),
welches auf V und M
verschiebbar ist.
Soll mit dem justirten Instrumente eine Entfernung AO
(Fig. 6) gemessen werden, so stellt der Beobachter in A das Stativ mit eingelegtem Fernrohre auf, visirt das
Object O an und läſst rechts von I in der durch D fixirten
Richtung in der Entfernung von 25m von dem
Gehilfen das Stativ II aufstellen; nun richtet der
Gehilfe den Visirstab V gleichfalls nach demselben von
A aus anvisirten Punkte des Objectes O und verschiebt das auf V
aufgehängte Zielschildchen Z so lange, bis das weiſse
Feld f desselben von dem Verticalfaden des Fadenkreuzes
des in I liegenden Fernrohres halbirt wird, und liest
am Zeiger den Stand des Schildchens auf der Theilung des Visirstabes (in Fig.
14 z.B. 42,5) ab. Hierauf wechseln der Beobachter und der Gehilfe die
Plätze; letzterer legt den Meſsstab so in das Lager des Statives I ein, daſs ein an demselben angebrachter Indexstrich
i (Fig. 12)
dieselbe Lesung auf der Messingschiene s gibt, welche
vorher am Visirstabe erhalten wurde (also 42,5); der Beobachter legt das Fernrohr in
das Lager des Statives II ein, visirt das Object O an und läſst das Zielschildchen auf dem Meſsstabe so
lange verschieben, bis dessen weiſses Feld von dem auf O eingestellten Verticalfaden halbirt wird, wonach von den Gehilfen ohne
weiteres die Entfernung (2500m) abgelesen
wird.
Die Compensationsvorrichtung dient zur Ausführung der früher erklärten Verschiebung des
Meſsstabes; dieser muſs aber in richtiger Weise mit der Messingschiene verbunden
sein, so zwar, daſs bei Messung der bekannten Entfernung D1 diese auch nach erfolgter Verschiebung,
bezieh. nach der erfolgten Einlegung des Meſsstabes bei der am Visirstabe gemachten
Lesung erhalten wird.
Vorausgesetzt, daſs der Meſsstab richtig getheilt ist, daſs das
Fadenkreuz des Fernrohres berichtigt ist (die diesbezüglichen Prüfungen sind leicht
vorzunehmen), haben auf die Ermittlung der Entfernungen zwei Fehler Einfluſs: der
reine Distanzmessungsfehler, hervorgerufen durch Fehler im Visiren, Einstellen und
Ablesen, und der Fehler in Folge der fehlerhaft aufgetragenen Basis.
Der reine Distanzmessungsfehler wächst im quadratischen
Verhältnisse zur Distanz, so daſs f_1=\mu D^2 gesetzt werden
kann; aus 500 Messungen von Entfernungen, welche zwischen 830,1 und 7828m,7 liegen und aus einer gröſseren sorgfältig
ausgeglichenen Triangulirung genommen wurden, ergab sich:
{f_1}^m=0,000001874\,D^2 oder in
Procent p_1=0,0001874\,D.
Der Fehler wegen der Basis steht im einfachen Verhältnisse zur
Distanz und nimmt natürlich mit der Ungenauigkeit der Basis zu. v. Paschwitz gibt seinem Instrumente zum Auftragen
derselben eine Meſsschnur bei, bei deren Benutzung der Fehler
f_2=v\,b aus 400 Messungen mit
{f_2}^m=0,00877\,D oder in Procent
p_2=0,877 abgeleitet wurde, was einem mittleren Fehler von
22cm in der Absteckung der Basis
gleichkommt.
Bedient man sich jedoch zum Auftragen eines Stahlmeſsbandes, so
wird {f_2}^m=0,00326\,D oder in Procent 0,326, wodurch der
mittlere Fehler des Basis sich mit 8cm ergibt.
Da bei allen Entfernungen unter 4696m der Fehler wegen der Basis, wenn man die Schnur benutzt, gröſser als der
reine Distanzmessungsfehler wird und solche Entfernungen gerade in der
Artilleriepraxis vorkommen, so soll die Schnur ganz vermieden werden und nur das
Stahlmeſsband zur Verwendung kommen.
Der mittlere Gesammtfehler ist schlieſslich
F^m=\sqrt{{f_1}^2+{f_2}^2} oder in Procent
P=\sqrt{{p_1}^2+{p_2}^2}, wonach sich folgende Tabelle leicht
ergibt:
a) Benutzung des
Stahlbandes
b) Benutzung der Schnur
m
m
m
m
D =
1000
F =
4
P =
0,4 %
D =
1000
T =
9
P =
0,9 %
2000
10
0,5
2000
19
1,0
3000
20
0,7
3000
32
1,1
4000
33
0,8
4000
47
1,2
5000
50
1,0
5000
65
1,3
6000
71
1,2
6000
86
1,4
7000
96
1,4
7000
112
1,6
8000
125
1,6
8000
141
1,8
9000
157
1,7
9000
174
1,9
10000
193
1,9
10000
209
2,1
Durch die Wahl einer gröſseren Basis, wodurch übrigens auch die
Theilung des Stabes abgeändert wird, könnte man noch geringere Fehler erzielen;
allein den Bedürfnissen der Praxis entspricht eine längere Basis nicht und dürfte
man mit 25m schon an die zulässige Grenze gekommen
sein.
Es gewährt aber der behandelte Distanzmesser in seiner gegenwärtigen Einrichtung eine
solche Genauigkeit, daſs behauptet werden kann, derselbe entspricht den an ihn
gestellten Anforderungen vollständig und verdient, trotz Erforderniſs einer
Basisabsteckung, mit Rücksicht auf sein geringes Gewicht (12k), seine einfache Handhabung und den geringen
Zeitaufwand, welchen eine Messung beansprucht (etwa 3½ Minuten), in die
artilleristische Praxis eingeführt zu werden.
Tafeln