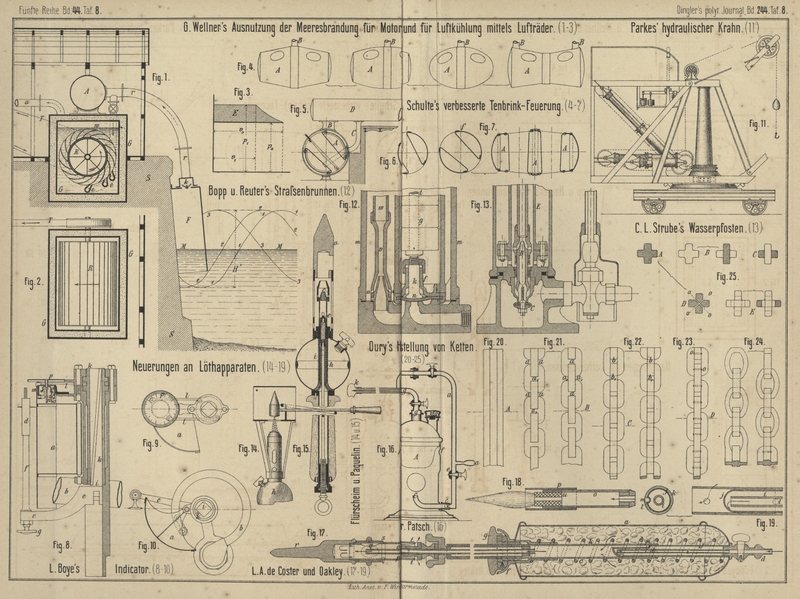
| Titel: | Die Brandung des Meeres, benutzt für motorische Zwecke und für die Erzeugung von kalter Luft mittels Lufträdern; von Georg Wellner, Ingenieur und o. ö. Professor an der k. k. technischen Hochschule in Brünn. |
| Autor: | Georg Wellner |
| Fundstelle: | Band 244, Jahrgang 1882, S. 100 |
| Download: | XML |
Die Brandung des Meeres, benutzt für motorische
Zwecke und für die Erzeugung von kalter Luft mittels Lufträdern; von Georg Wellner,
Ingenieur und o. ö. Professor an der k. k. technischen Hochschule in Brünn.
Mit Abbildungen auf Tafel 8.
G. Wellner's Ausnutzung der Meeresbrandung.
Die bewegte See mit ihren oft hochgehenden Wogen repräsentirt einen groſsartigen
angesammelten Vorrath von lebendiger Kraft. Der Windstoſs trifft den weiten
Wasserspiegel, macht den Ocean auf- und niederschaukeln und hebt die rollenden
Wellenberge, welche sich dann am Ufer brechen, nicht selten mit schäumendem Getose
und mit einer Gewalt, vor welcher die festesten Fundamente beben. „Die Elemente
hassen das Gebild der Menschenhand“; aber der Mensch begnügt sich nicht
damit, diese Einwirkungen der feindlichen Natur nach Möglichkeit abzuschwächen, er
geht noch weiter und sucht diese elementaren Kräfte selbst zu fassen, sie zu zähmen
und seinem Willen dienstbar zu machen. Im Anschlüsse an die vielfachen schon
bekannten Bemühungen, die Bewegung des Meerwassers für nützliche Arbeiten zu
verwerthen (die wechselnde Ebbe und Fluth zum Betrieb von Wasserrädern und Turbinen,
den Wellengang auf hoher See zur Fortbewegung der Fahrzeuge u. dgl. zu verwenden),
erlaubt sich der Verfasser durch den nachfolgenden Aufsatz eine einfache Methode in
Vorschlag zu bringen, wie die Brandung am Meeresufer mittels gewöhnlicher
Zellenräder für Luft zum Zwecke motorischer Arbeiten sowie zur Gewinnung von Kälte
ausgenutzt werden kann.
Längs der Strandmauer S (Fig. 1 Taf.
8) ist in passender Höhe über der normalen Meeresoberfläche M ein Luftfänger F festgemacht, auf dessen
Scheitel selbstthätige, nach oben sich öffnende Klappen k angebracht sind, ober welchen dann eine Windleitung r zu einem Accumulator (Windsammler oder Luftkessel)
A weiterführt. Wenn sich nun bei bewegter See Welle
um Welle in den wechselnden Lagen 1, 2, 3 gegen das
Ufer heranwälzt, so füllt sich bei 1 der Luftfänger F mit Luft, indem das Wellenthal unter die vordere
Unterkante desselben zu liegen kommt, bei 2 schlieſst
die Welle den Luftfänger nach auſsen ab und bei 3
lastet der Wellenberg vor dem Luftfänger über der innen abgeschlossenen Luft, so
daſs diese Luft verdichtet werden und zum Theil durch die sich hebenden Klappen k nach dem Accumulator abströmen muſs. Dieses Spiel
erneut sich mit jeder brandenden Welle und sammelt bei hinlänglicher Breite des
Windfangers eine wünschenswerthe groſse Luftmenge stoſsweise im Accumulator an.
Die erzielte Compression hängt
wesentlich ab von dem verticalen Abstand zwischen Wellenberg und Wellenthal H' und beträgt, nachdem 1at mit dem Drucke einer Säule reinen Wassers von 10m,334
Höhe, oder einer SeewassersäulenhöheDas specifische Gewicht des Seewassers variirt mit dem Salzgehalte zwischen
1,02 bis 1,04. von rund 10m,
gleichwertig ist, in Atmosphären Ueberdruck:
p_r=\frac{\eta'\,H'}{10}, . . . . . . .
. (1)
folglich in Atmosphären absoluter Spannung, wenn p0 der äuſseren
atmosphärischen Spannung entspricht:
p'=p_r+p_0=\frac{\eta'\,H'}{10}+p_0 . .
. . . . (2)
in welchen Ausdrücken der Factor η' jenen Bruchtheil der maximalen Spiegeldifferenz H' bezeichnet, welcher beim Eintritt der verdichteten
Luft durch die Klappen zur Wirkung gelangt.
Für einen günstigen Mittelwerth η' =
0,75 erzeugen nach Gleichung (1):
Wellen von
H'
=
1
2
3
4
5
6m
Höhe
Luftverdichtungen von
pr
=
0,075
0,150
0,225
0,300
0,375
0,400at.
Auf die beschriebene Weise füllt sich der Accumulator A
mit verdichteter Luft an und bildet einen Arbeitsvorrath, der sich weiter benutzen
läſst. Der Ueberdruck dieser angesammelten Luft würde hinreichend stark sein, um
dieselbe als Gebläsewind für Schmiede- und Frischfeuer, sowie für den Cupol- und
Hochofenbetrieb brauchen zu können; es ist dies jedoch unthunlich, weil die
Eisenerzeugung stetigen ununterbrochenen Gang verlangt, während die Windlieferung
hier durch den häufigen Wetterwechsel groſsen Ungleichförmigkeiten unterworfen ist.
Für den vorliegenden Fall sind also nur solche Fabrikationsrichtungen ins Auge zu
fassen, für welche Pausen im Betrieb und Veränderungen im Arbeitseffect zulässig
sind, und selbst da stellt sich eine Schwierigkeit der Ausführung entgegen. Die
gewöhnlichen Cylindermaschinen mit hin- und hergehendem Kolben sind nämlich nicht im
Stande, die geringfügigen Ueberdruckspannungen von 0,1 bis 0at,4 nutzbar zu machen, weil die Widerstände
(insbesondere die Kolbenreibung) zu ihrer Bewältigung, also für den Leergang dieser
Maschinen allein schon rund 0at,5 Ueberdruck
erfordern, folglich ein effectiver Arbeitsgewinn ganz unmöglich wird.
In vorzüglicher Weise eignen sich dagegen zur ökonomischen Verwerthung der kleinen
Spannungsdifferenzen im vorliegenden Falle die sogen. Lufträder. Es sind dies gewöhnliche Zellenräder R (Fig. 1 und
2 Taf. 8), welche unter Wasser stehen und in deren Zellen die von unten
eintretende Luft vermöge ihres Auftriebes hebend wirkt. Die Luft strömt bei e in die tiefstliegenden Zellen ein, verdrängt das
Wasser daraus, expandirt hierauf während der Drehung des Rades, den Zellenraum immer
mehr ausfüllend in dem Maſse, als die Zellen hinaufsteigen, bis sie sich endlich in
den Luftraum ober dem Wasserspiegel w ausgieſst. Dieser
Vorgang wiederholt sich für alle Zellen nach einander bei stetigem Lufteintritt von
unten. Die dabei geleistete mechanische Arbeit besteht in der Hebung des specifisch
leichten Luftkörpers in dem schwereren Wasser auf der emporsteigenden Radseite oder, was auf das
nämliche herauskommt, in dem Herabsinken des Ueberschusses an Wasser in den Zellen
der zweiten heruntergehenden Seite. Die Expansionswirkung der Luft gelangt durch das
allmähliche Zurückdrängen des Wassers aus den Zellen voll zur Geltung.
Diese LufträderVgl. Armengaud Ainé: Les Progrès de l'Industrie à
l'Exposition universelle à Paris 1867, Bd. 1 S. 64.,
eigentlich Luftexpansionszellenräder, bilden eine Umkehrung der
Luftcompressionszellenräder oder Zellenradgebläse (vgl.
1880 236 * 444) und sind in ihrer Wirkungsweise auch
vollständig analog den oberschlächtigen Wasserrädern,
wobei nur Wasser mit Luft und oben mit unten vertauscht erscheint. Die
Arbeitsverluste beim Betrieb der Lufträder bestehen vornehmlich in der Wasserreibung
und in der Achsenreibung und betragen immer nur Bruchtheile der theoretischen
Arbeitsfähigkeit, so daſs der Gang dieser Lufträder vollkommen sicher ist. – Auch
für eine Spannungsdifferenz von nur 0at,1 oder
1m Wassersäule wird der Umlauf des Rades mit
gutem Nutzeffect vor sich gehen. Die weitere Transmission T der Effectivleistung dieser Lufträder geschieht am besten durch die
Radachse selbst, wie aus Fig. 2 zu
ersehen ist.
Die von den Lufträdern gelieferte Arbeit ist bedingt durch das zu
Gebote stehende Volumen sowie durch die Pressung der Luft im Accumulator und richten
sich hiernach die passenden Dimensionen. Heiſsen wir:
D den Auſsendurchmesser des
Zellenrades in m,
a, b die Zellen tiefe und Zellen
breite in m,
f den mittleren
Füllungscoefficienten und
c die secundliche
Umlaufsgeschwindigkeit des Zellenmittels in m,
dann beträgt das zur Wirksamkeit gelangende, Auftrieb
schaffende, mittlere Luftvolumen, welches das Wasser in den emporsteigenden Zellen
verdrängt, offenbar:
V=f\,a\,b\,c . . . . . . . . . . (3)
Bezeichnet ferner:
H die erzielte mittlere Hubhöhe in
den Zellen,
γ das specifische Gewicht des
Wassers und
η den
Nutzeffectscoefficienten,
so beträgt die effective Arbeitsleistung der Lufträder
in Pferdestärken:
N=\eta\,\frac{V\,H\,\gamma}{75} . . . .
. . . . (4)
Es ist dies ein Ausdruck identisch mit jenem, welcher bei
Wasserrädern, sowie bei allen hydraulischen Motoren gültig ist, in welchem Falle V das zuflieſsende Wasservolumen und H das Gefälle bedeuten würde.
Unter Annahme der concreten Werthe und Verhältnisse:
\eta=0,8,\ f=0,5,\ a=0,125\,D,\ c=2,\ H=0,75\,D und
\gamma=1000 folgt N=bD^2; ein Luftrad von
beispielsweise 2m Durchmesser und 3m Breite würde effectiv 12e leisten. Die Gröſsen V und H in der Arbeitsformel (4) stellen
Mittelwerthe zweier Veränderlichen v und h dar, deren Abhängigkeit von einander bekannt sein
muſs, wenn man die Mittelwerthe genau ermitteln soll. Das von der Luft in den
hinaufgehenden Zellen verdrängte Wasservolumen v ist
nämlich infolge der auftretenden Expansion variabel und aus demselben Grunde auch
die Hebungshöhe h der betreffenden Partie. Die
differentiale Arbeit besteht in der Hebung eines verdrängten Wasserkörpers v um die unendlich kleine Höhe dh, die Gesammtleistung beträgt somit in Meterkilogramm:
E=V\,H\,\gamma=\int\,v\,\gamma\,d\,h .
. . . . . (5)
in welchem Integral noch die Function zwischen v und h einzuführen
ist.
Anstatt der Wassersäulenhöhen h
wollen wir, wie es für die Rechnung bequemer ist, die specifischen Spannungen der
Luft in die Formel bringen.
Wir nennen:
p diese variable Luftspannung in
den aufsteigenden Zellen, gemessen in k/qm, ferner
p1,p0 die
Luftspannungen beim Eintritt unten und beim Austritt ober dem Wasserspiegel
und
v1,v0 die Luftvolumen
beim Ein- und Austritt in cbm für die Secunde; dann ist:
\gamma\,h=p-p_0 und
\gamma\,d\,h=d\,p
und das Arbeitsintegral (5) erhält die bekannte Form
(s. das Arbeitsdiagramm Fig. 3):
E=\int\,v\,d\,p . . . . (6)
Nachdem das Luftrad in einem Wassergefäſs umläuft, sind wir voll
berechtigt, anzunehmen, daſs die Zustandsänderungen der Luft in den Zellen bei
constant bleibender Temperatur, also nach der isothermischen, hyperbolisch
verlaufenden Expansionslinie vor sich gehen. In diesem Falle gilt die Relation:
p_v=p_1\,v_1=p_0\,v_0 . . . . . . . . .
. . (7)
und das Integral löst sich einfach zwischen den Grenzen
p1 und p0:
V\,H\,\gamma=E=p_0\,v_0\,log\,nat\,\left(\frac{p_1}{p_0}\right),
. . . . . (8)
welcher Ausdruck, in die Arbeitsgleichung (4)
eingesetzt, liefert:
N=\eta\,\frac{p_0\,v_0\,log\,nat\,(p_1\,:\,p_0)}{75} . . .
. . . . . (9)
Mit Einführung der speciellen Werthe η = 0,75 und p0 = 10334 erhält man hieraus, das nöthige Volumen der aus dem
Wasserspiegel ober dem Zellenrade heraustretenden Luft für 1e und Stunde:
\frac{3600\,v_0}{N}=\frac{32,5}{log\,nat\,(p_1\,:\,p_0)} . .
. . . . . . . . (10)
Es ergibt sich f. d. Luftverdicht.:
p_r=p_1-p_0 = 0,10 0,15 0,20 0,25 0,30at
d. i. für die Spannungsverhältnisse:
p_1\,:\,p_0 = 1,10 1,15 1,20 1,25 1,30
ein stündlicher Luftbedarf für 1e: \frac{3600\,v_0}{N} = 341,0 232,0. 176,8. 145,8.
123,6cbm.
Durch die Gleichungen (3), (4) und (10) sind nun hinlängliche
Anhaltspunkte für die Betriebskraft der Lufträder gegeben, zumal ihre Wirkungsweise
derjenigen der Wasserräder vollkommen gleichkommt. Derselben Analogie lassen sich
auch die Constructionsverhältnisse entnehmen.
Hinsichtlich der praktischen Anordnung der Lufträder bei der vorliegenden Art der
Luftbeschaffung durch den Wellengang des Meeres erscheint es zweckmäſsig, die
Einrichtung so zu treffen, daſs man mit verschiedenen Compressionsgraden arbeiten
könne. Zu diesem Behufe führt das Windleitungsrohr (vgl. Fig. 1) vom
Accumulator A, welcher aus örtlichen Gründen oben auf
dem Luftradgefäſs G aufgestellt ist, in verschiedene
Wassertiefen herab zu mehreren Düsenauslässen e mit
gesonderten Absperrventilen, so daſs man die Luft an höheren oder tieferen Stellen
des Radumfanges in die Zellen ausblasen lassen kann. Auſserdem ist der Wasserstand
w zwischen gewissen Grenzen regulirbar zu machen,
damit ein groſser Spielraum für die von der Preſsluft beim Emporsteigen in den
Zellen zu durchsetzenden Wassersäulenhöhen gewonnen werde. Wenn die Luft in Folge
niedriger Wellen und kleiner Verdichtung die unterste Düsenmündung nicht zu
erreichen vermag, sondern weiter oben austreten muſs, dann wird der Auftrieb
natürlich nur auf dem restlichen Theil der Radhöhe wirksam, ganz ähnlich so wie bei
rückenschlächtigen Wasserrädern, bei welchen das Gefälle kleiner ist als der
Raddurchmesser.
Neben der motorischen Arbeitsleistung läſst sich bei dem
Lufträderbetrieb noch ein anderer Zweck mit verbinden, nämlich die Kühlung der
Luft, welcher Umstand natürlich nur dort in Betracht kommt, wo eine solche
Kühlung für die betreffenden Fabrikanlagen wünschenswerth und ersprieſslich ist
(z.B. für Bierkellereien, Fleischvorrathsmagazine u. dgl. in südlichen Ländern). Die
Expansion der Luft in den emporsteigenden Zellen des Luftrades erzeugt nämlich eine
Abkühlung des umgebenden Wassers.
Wenn sich die Luft in einem vollkommen wärmedichten Gefäſs ausdehnt, so daſs von
auſsen weder Wärme zu-, noch abgeführt wird, dann fällt die Spannung der Luft in
rascherem Maſse, als das Volumen sich vergröſsert; es sinkt auch die Temperatur, und
zwar verläuft diese Zustandsänderung bekanntlich nach dem potenzirten Mariotte'schen
Gesetze und der Spannungsabfall verfolgt die adiabatische Linie, welcher die
Function: p0
v0k = p1
v1k = pvk = Const zu Grunde
liegt. Bei der Rotation des Luftrades steht jedoch die Sache anders. Die in den
Zellen befindliche Luft steht mit den Zellenwänden und dem umgebenden Wasser in
inniger Berührung und nimmt jene Temperatur an, welche im Luftrad gefäſs e herrscht. Das Wasser circulirt stetig im Gefäſse,
vermischt die kälteren Partien mit den wärmeren und der sich bald einstellende
allseitige Temperaturausgleich wird endlich jene Temperatur herausbilden und
festhalten, bei welcher ein Beharrungszustand zwischen der zu- und abgeleiteten
Wärmemenge besteht. Aus dem eben angeführten Grunde waren wir bei den früheren
Berechnungen vollkommen berechtigt, anzunehmen, daſs die Expansion der Luft im
Luftrade bei constanter Temperatur vor sich gehe. Die Ausdehnung der Luft bei
gleichbleibender Temperatur erfordert aber eine gewisse von auſsen hinzukommende
Wärmemenge, welche in unserem Falle dem Wasser im Luftrad gefäſse entzogen wird,
folglich abkühlend wirkt. Die Temperatur dieses Wassers sowie des Radkörpers und der
inneren Gefäſswände wird allmählich herabsinken bis zu einer durch den oben
erwähnten Beharrungszustand bestimmten Grenze. Diese Grenze wollen wir jetzt
bestimmen und zwar unter der Voraussetzung, daſs das Luftradgefäſs mittels doppelter
Holzwände und Wärme schlecht leitender Zwischenfüllung so hinreichend wärmedicht
gemacht sei, daſs die Wärmetransmission an der Oberfläche von auſsen nach innen
vernachlässigt werden darf.
Die Wärmemenge, welche für die Expansion der Luft bei
gleichbleibender Temperatur entzogen werden muſs, ist nach der mechanischen
Wärmetheorie bekanntlich genau äquivalent mit der dabei nach auſsen verrichteten
Arbeitsleistung. Die dem Wasser im Luftradgefäſs entzogene Wärmemenge beträgt somit,
da 1c mit 424mk
gleichwertig ist, in Calorien:
W=\frac{p_0\,v_0\,log\,nat\,(p_1\,:\,p_0)}{424} . . . . .
(11)
Dieser Abkühlung entgegen wirkt die Erwärmung, welche dadurch
herbeigeführt wird, daſs die unter das Zellenrad eintretende Luft wärmer ist als das
Wasser und folglich ihre Temperatur mit jener des Wassers ausgleicht. Heiſsen
wir:
t1
diese Temperatur der eintretenden Luft (es wird das nahezu immer die Temperatur
der äuſseren freien Luft sein),
t0
die allmählich erzielte niedrigere Temperatur des Wassers im Luftradgefäſs (es
ist dies auch die Temperatur, welche die Luft nach dem Austritt aus der Düse
annimmt und während der Expansion und bei dem Austritt über dem Wasserspiegel
beibehält),
c die specifische Wärme der Luft
bei constanter Spannung und
γ0
das specifische Gewicht der austretenden Luft,
so beträgt die Erwärmung durch den Eintritt jener
Luftmenge, welche beim Austritt oben ein Volumen V0 besitzt, in Calorien:
W_1=v_0\,\gamma_0\,c\,(t_1-t_0) . . . .
(12)
Für den einmal eingetretenen Beharrungszustand in der
Wärmezu- und abfuhr haben wir zu setzen:
W=W_1 . . . . . . . . (13)
und man findet aus der Gleichsetzung der Ausdrücke (11)
und (12) die erzielte Abkühlung der Luft beim Durchgang durch das Luftrad:
t_1-t_0=\frac{p_0\,log\,nat\,(p_1\,:\,p_0)}{424\,\gamma_0\,c}
. . . . (14)
Mit Einsetzung der Werthe p_0=10334,\ c=0,23751
und y_0=1,294 (was zulässig erscheint, weil die Temperatur t0 jedenfalls nahe 0°
liegen muſs) erscheint:
t_1-t_0=79,3\,log\,nat\,(p_1\,:\,p_0) .
. . . (15)
somit für die Expansionsgrade:
\frac{p_1}{p_0}
=
1,10
1,15
1,20
1,25
1,30
d. i. für die Wassersäulenhöhen:
H
=
1,0
1,5
2,0
2,5
3,0m
eine erzielte Luftabkühlung:
t_1-t_0
=
7,55
11,06
14,45
17,69
20,80°.
Aus den Zahlen der letzten Reihe folgt das Resultat, daſs man die Luftabkühlung nur
für höhere Expansionsgrade oder für niedrigere Temperaturen der äuſseren Luft bis
unter den Eispunkt herab zu bringen im Stande ist. So muſs z.B. für eine
Auſsentemperatur t1 =
20° die im Luftradgefäſs durchsetzte Wassersäulenhöhe H
schon 3m betragen, wenn man Luft von t0 = 0° erhalten soll;
für t1 = 14° genügt zu
dem gleichen Ziel H = 2m. Die kalt gewordene Luft tritt schlieſsllich oben aus dem Gefäſs G heraus und wird durch wärmedicht verwahrte Rohre a zum Orte ihrer Bestimmung hingeführt. Wenn durch
günstige örtliche Verhältnisse so hohe Luftpressungen zur Verfügung stehen, daſs die
Abkühlungen unter 0° möglich, also unter Umständen zur Eiserzeugung benutzt werden
könnten, dann muſs natürlich zum Schütze gegen das Einfrieren im Luftradgefäſs
anstatt des gewöhnlichen Wassers eine entsprechende Salzlösung mit niedrigerem
Gefrierpunkt gewählt werden. Eine derartige Sachlage bildet freilich nur einen
auſsergewöhnlichen Ausnahmsfall; aber es bleibt auch für die normalen Aufstellungen
immerhin beachtenswerth, daſs das Luftrad neben der motorischen Arbeit auch noch
eine groſse Menge frischer kalter Luft liefert, welche für verschiedene Zwecke
wünschenswerth und vortheilhaft sein kann.
Tafeln