| Titel: | Ch. Burrell's Regulator. |
| Autor: | Whg. |
| Fundstelle: | Band 250, Jahrgang 1883, S. 190 |
| Download: | XML |
Ch. Burrell's Regulator.
Mit Abbildungen auf Tafel 14.
Ch. Burrell's Regulator.
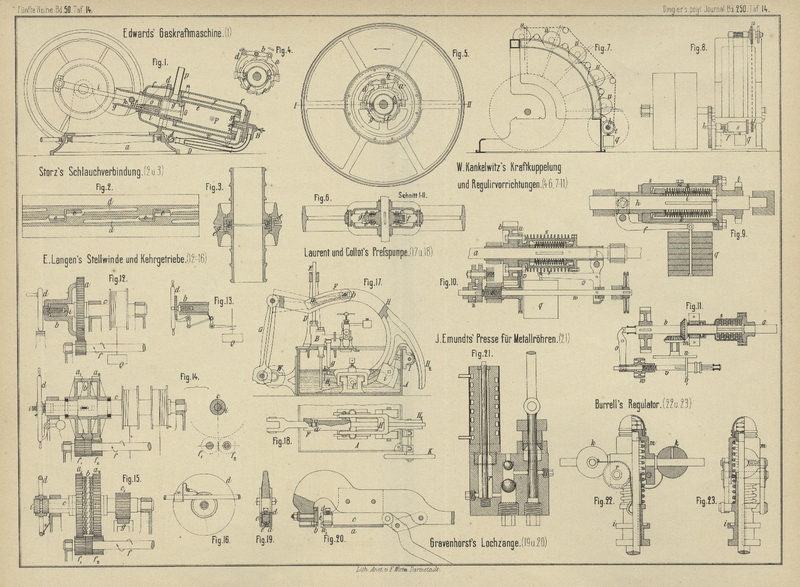
Der in Fig. 22 und 23 Taf. 14
nach Engineering, 1883 Bd. 36 S.
105 dargestellte Centrifugalregulator von Ch.
Burrell und Söhne in Thetford (Englisches Patent Nr. 5813 vom 6. December
1882) ist in so fern eigenartig, als er gar keine Gelenkverbindungen besitzt. Die
Kugeln k werden auf Bolzen geführt, welche in einer auf
das obere Ende der Regulatorspindel aufgeschraubten Kappe m senkrecht zur Spindel befestigt sind. Die Hülse i hängt an zwei Stahlbändern, welche, über Rollen r geführt, beiderseits an die Kugeln k
angehängt sind. Eine kräftige, oben gegen m sich
stützende Schraubenfeder bildet die Hülsenbelastung.
Abgesehen von der Reibung, dem Hülsengewichte und der unbedeutenden Neigung der
Stahlbänder muſs hier die Centrifugalkraft der beiden Kugeln immer gleich der
Spannung der Belastungsfeder sein, welche sich proportional der Verschiebung der
Hülse, d.h. dem Ausschlage der Kugeln ändert. Ist also G das Gewicht einer Kugel, r der Abstand der
Kugelmittelpunkte von der Wellenmittellinie, w die
Winkelgeschwindigkeit und F die veränderliche
Federspannung, so ist:
2\,\frac{G}{g}\,r\,w^2=F oder
w^2=\frac{1}{2}\ \frac{F}{r}\ \frac{g}{G}
Der Regulator wird mithin vollkommen astatisch sein, wenn F : r constant bleibt,
d.h. wenn die Federspannung F stets dem Radius r direkt proportional ist, also F = cr, unter c eine Constante verstanden.
Dies ist der Fall, wenn die Feder eine solche Länge hat, daſs sie gerade vollständig
entlastet wäre, wenn die Kugelmittelpunkte in der Wellenmitte angekommen wären,
falls dies möglich sein würde; oder mit anderen Worten, wenn die ganze
Zusammendrückung der Feder für eine bestimmte Lage der Kugeln gleich dem
betreffenden Abstande r ist. Ist die Feder im
unbelasteten Zustande um die Strecke a kürzer, als
obiger Bedingung entspricht, so ist: F=c\,(r-a), also
F\,:\,r=c\,\left(1-\frac{a}{r}\right); der Quotient F : r, also auch w2 ist daher in diesem Falle um so
gröſser, je gröſser r ist, und jedem Werthe von r wird ein bestimmter Werth der Winkelgeschwindigkeit
entsprechen, welcher nach der Gleichung w^2=\frac{1}{2}\
\frac{g}{G}\,c\,\left(1-\frac{a}{r}\right) zu berechnen ist.
Der Regulator ist also dann stabil (statisch) und zwar in um so höherem Grade, je
gröſser a ist. Selbstverständlich muſs a immer kleiner bleiben als der kleinstmögliche Werth
von r. Im entgegengesetzten Falle, wenn die unbelastete
Feder um eine Strecke b länger ist, als dem
indifferenten Gleichgewichte entspricht, so ergibt sich in gleicher Weise, daſs der
Regulator bei keiner Geschwindigkeit im Gleichgewichte sein kann, also labil ist und
zwar in um so höherem Grade, je gröſser b ist. Eine
Gewichtsbelastung würde einer unendlich langen Feder entsprechen, ist also gänzlich
unbrauchbar.
Der Regulator ist hiernach in so fern recht zweckmäſsig, als er eine bequeme
Einstellung auf einen gewünschten Stabilitätsgrad ermöglicht. Fraglich ist nur die
Dauerhaftigkeit der Stahlbänder. Auch wird durch die Reibung der Kugeln auf den
Führungsstangen der Empfindlichkeitsgrad beeinträchtigt.
Whg.
Tafeln