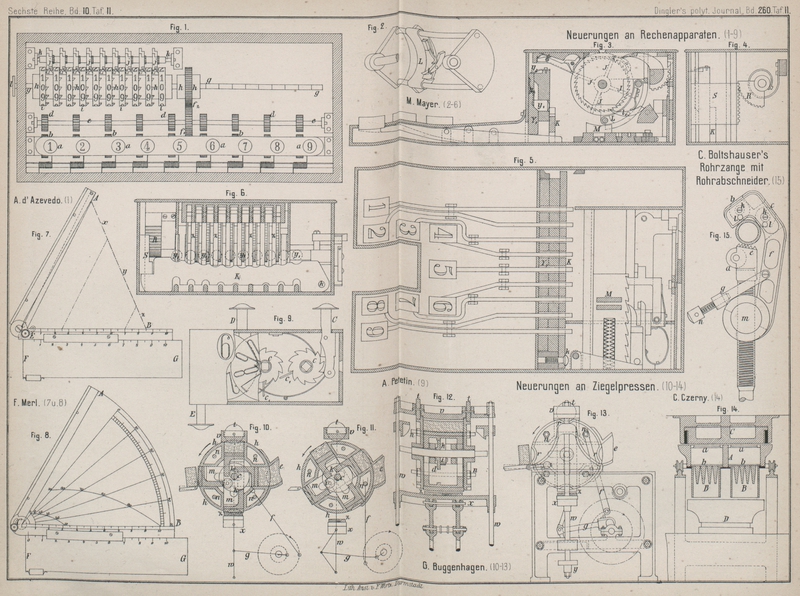
| Titel: | Ueber Neuerungen an Rechenapparaten. |
| Fundstelle: | Band 260, Jahrgang 1886, S. 167 |
| Download: | XML |
Ueber Neuerungen an Rechenapparaten.Vgl. Neuerungen an Rechenapparaten: v. Arbter 1876
220 * 511. A. Poppe
1877 223 * 152. S.
Claparède 1877 226 * 345. Chambon 1878 228 184.
Leuner 1879 231 *
326. G. Fuller 1879 233
* 208. Thomas 1879 234
248. 1881 239 322. Sheppard 1880 235 323. Wüst 1880 237 * 364. Ruth 1881 242
149.
Patentklasse 42. Mit Abbildungen im Texte und auf
Tafel 11.
Ueber Neuerungen an Rechenapparaten.
Der Reckenapparat von C. Jul. Giesing in
Döbeln (* D.
R. P. Nr. 26107 vom 31. Juli 1883) bezweckt die Erleichterung der
Ausführung von Zahlenrechnungen nach jener Methode, wie sie geübtere Rechner wohl
ohne jeden Apparat anzuwenden pflegen.
Sind z.B. zwei Zahlen gegeben, die man mit einander zu multipliciren hat (vielleicht
\overrightarrow{352}\,\times\,\overleftarrow{436}), so kann
man das Product Zahl für Zahl, von den Einern ausgehend, unmittelbar daneben
schreiben, wenn man in folgender Weise verfährt: Man multiplicirt zuerst alle
Zahlen, welche Einer ergeben (2 × 6 = 12); die Einer der gesuchten Endzahl würden
also 2 betragen. Die überschieſsenden Zehner (1) fügt man dem Producte der Zahlen
zu, welche Zehner ergeben (1 + 5 × 6 + 2 × 3 = 37, die Zehner der Endzahl wären
somit 7); die überschieſsenden Hunderter (3) wiederum dem Producte der Ziffern,
welche Hunderter ausmachen (3 + 3 × 6 + 5 × 3 + 2 × 4 = 44), u.s.f.
Fig. 1., Bd. 260, S. 167 Wie zu sehen, benutzt man die Ziffern des Multiplicanden von links nach
rechts, die des Multiplicators von rechts nach links, was einige Aufmerksamkeit
erfordert. Um nun in beiden Zahlen nach derselben Richtung vorgehen zu können und
die zu multiplicirenden Ziffern unmittelbar über einander zu haben, wendet Giesing den durch Textfig.
1 wiedergegebenen Apparat an. Es ist A eine
durch senkrechte Gerade in Reihen (Aa bis Aq) getheilte gröſsere festliegende Schreibfläche als
Ort des Multiplicanden bei der Multiplication bezieh. des Dividenden und Radicanden
bei der Division und dem Wurzelziehen; B bedeutet die
in gleich viel Reihen (Ba bis Bq) getheilte kleinere Schreibfläche als Ort für das Ergebniſs genannter
Rechnungsarten; C bezeichnet die in Abtheilungen von gleicher
Breite getheilte, wagerecht in AB verschiebbare Leiste
mit Schreibfläche als Ort für den in umgekehrter
Ziffernfolge niederzuschreibenden Multiplicator bezieh. Divisor; D endlich ist der zur Befestigung der verschiebbaren
Leiste dienende Riegel, der vor Beginn des Gebrauches nach abwärts zu drücken
ist.
Der Apparat ist in Textfig. 1 in der Stellung für die
letzte der oben angegebenen Ausrechnungen gezeichnet. Für die nächst zu bestimmende
Ziffer würde also die Leiste um eine Theilung nach links geschoben und dann die unter einander stehenden Zahlen mit einander
multiplicirt werden, also 4 + 3 × 3 + 4 × 5 = 33; als letzte Ausführung endlich nach
abermaliger Schiebung erscheint: 3 + 4 × 3 = 15, d.h. Gesammtergebniſs 153472.
Aehnlich wie bei der Multiplication ist das Verfahren bei der Division. Der in
umgekehrter Ziffernfolge geschriebene Divisor wird dabei von links nach rechts
schrittweise vorwärts geschoben, so daſs man immer die Zahlen unmittelbar über
einander hat, welche zusammen abzuziehen sind.
Der Apparat wird auch als Kreisscheibe ausgeführt, wobei die verschiebbare Leiste in
einen sich drehenden Ring übergeht.
Die Rechenmaschine von C. T. Mauersberger in Glauchau (* D. R. P. Nr.
26756 vom 28. Oktober 1883) besteht aus einer Productentafel, welche auf dem Umfange einer drehbaren Trommel t (Textfig. 2)
angebracht ist. Eine feststehende Multiplicandenreihe dient dazu, den mit Vorsprung
a versehenen verschiebbaren Zeiger z derart einzustellen, daſs die Bewegung der Tabelle
t an der mit einem Stifte i hervorgehobenen Quadratzahl der durch den Zeiger z angedeuteten Zahl gehemmt und dadurch die betreffende Productenreihe
rasch und sicher in die für die Ablesung nöthige Lage gebracht wird.
Fig. 2., Bd. 260, S. 168Peter
Wiesenmüller in Nürnberg (* D. R. P. Nr. 33155 vom 11. April
1885) hat eine ähnliche Productentafel mit einer
Federbüchse verbunden, welche als Lehrmittel dienen soll. Die Federbüchse
hat eine drehbare Hülse mit einem Ausschnitte, welcher einen Theil von auf dem
Umfange der Federbüchse angebrachten Zahlen sichtbar macht. Dieselben sind Producte
aus den Zahlen, welche auf der Hülse einerseits und auf der Federbüchse, neben der
Hülse, andererseits angebracht sind.
J. R. Brunner in Küsnacht bei Zürich vereinfacht
Multiplicationen bezieh. Divisionen mit einer gleichbleibenden Zahl dadurch, daſs er für Einer, Zehner, Hunderter u.s.w.
getrennte Producten- bezieh. Quotientenreihen auf dem Umfange von Kreisscheiben a (Textfig. 3) anordnet,
die jede für sich um ihre wagerechte Achse gedreht werden können, zu welchem Zwecke
sie mit vorstehenden Stiften versehen sind. Ein unbeabsichtigtes gegenseitiges
Mitnehmen der Scheiben ist durch die dazwischen gelegten Wände b verhindert. Die Multiplication bezieh. Division ist
somit durch die Addition der über einander gestellten Zahlenwerthe erreicht. Fig. 3 stellt
einen Apparat für Jahreszinsrechnungen zu 3¾ Proc. dar mit 5 Scheiben, welcher also
für Zinsberechnungen für ein Kapital bis zu 99999 M. genügt. So würden z.B. die
Jahreszinsen von 97306 M. die Summe der links liegenden Zahlenwerthe, also 3648 M.
97,5 Pf. betragen.
Fig. 3., Bd. 260, S. 169 Der Apparat ist sehr einfach und daher verständlich und die Zahlen können
zur Schonung der Augen in jeder gewünschten Gröſse, entsprechend der Dicke der
Scheiben, aufgetragen werden. Durch Anbringung von Decimalstellen läſst sich für
besondere Zwecke jede geforderte Genauigkeit erzielen.
Eine Anzahl neuerer Rechenapparate benutzen als Grundlage für das Rechnen die graphisch aufgetragenen Logarithmen, beruhen also auf
demselben Gedanken wie die logarithmischen Rechenschieber.
A.
Beyerlen in Stuttgart (* D. R. P. Nr. 31889 vom 16. Oktober
1884) bringt die logarithmischen Theilungen auf den Kreiscylinderflächen
von zwei gleich groſsen Scheiben an, welche so gelagert sind, daſs sowohl die eine
gegen die andere, als auch beide gemeinschaftlich gegen einen am Gestelle festen
Zeiger bewegt werden können. (Vgl. auch die Rechenscheiben von Prof. G. Herrmann und Sonne in
der Zeitschrift des Vereins deutscher Ingenieure, 1876
S. 721. 1877 * S. 455.)
Um eine weiter gehende Genauigkeit der Ablesungen und damit der Ausrechnungen zu
ermöglichen, wie mit Hilfe des gewöhnlichen Rechenschiebers zu erzielen ist, ersetzt
C.
Piper in Lemgo (* D. R. P. Nr. 25847 vom 25. Mai 1883) das Lineal des Rechenschiebers
durch eine Tafel, welche in gleiche senkrechte Streifen von geringer Breite getheilt
ist. Die Streifen sind links gleich getheilt und rechts ist an denselben die
Theilung der Zahlen zu den betreffenden gegenüber stehenden Logarithmen. Es
entspricht demnach z.B. einer Tafel von 100mm
Länge und 40mm Höhe, welche in 50 Streifen von
2mm Breite getheilt ist, einer Schieberlänge
von 2m, so daſs ein Logarithmus noch bis auf. die
vierte Stelle abgelesen werden kann.
Der Schieber, welcher also dazu dient, die Logarithmen entweder zu addiren oder zu
subtrahiren, ist durch einen „Zeigerapparat“ (vgl.
Textfig. 4) ersetzt, welcher für die
„Nulllage“ mit vier Spitzen a bis d auf die Eckpunkte der Tafel gelegt wird. Mit Hilfe
eines fünften Punktes e läſst sich nun die Länge jedes
beliebigen Logarithmus zwischen die Spitzen abnehmen; zu diesem Zwecke ist dieser
fünfte Punkt e durch eine Spitze gebildet, welche an
einer um einen Gestellpunkt drehbaren Stange verschiebbar ist.
Fig. 4., Bd. 260, S. 170 Will man nun z.B. multipliciren, so stellt man bei der Nulllage des
Rahmens den beweglichen Zeiger auf den Logarithmus der einen Zahl und verschiebt
hierauf den ganzen Rahmen parallel mit sich selbst, so daſs ein Eckpunkt auf den
Logarithmus der anderen Zahl kommt; dann muſs natürlich der Zeiger e auf dem Logarithmus des Productes stehen, da man
hiermit die beiden Logarithmen addirt hat. Es addiren sich bei dieser
Parallelverschiebung sowohl die wagerechten, als die lothrechten Verschiebungen. Bei
der Division wird der Unterschied der Logarithmen auf gleiche Weise gebildet. – Auch
die trigonometrischen Funktionen sind auf dieselbe Weise in gleichem Maſsstabe
aufgetragen und mit der Tafel der Logarithmen der Zahlen zu einem sehr gedrängten
Ganzen vereinigt worden.Der Preis einer solchen „vierstelligen graphischen
logarithmisch-trigonometrischen Tafel,“ welche die Gröſse eines
Octavblattes hat, ist 80 Pf., der dazu gehörige Zeigerapparat kostet 1,20
M., eine besondere Erläuterung 50 Pf. Auf Verlangen werden vom Erfinder auch
gröſsere Ausführungen hergestellt.
Etwas anders verfährt Max Kloth in Schleswig (* D. R. P.
Nr. 26695 vom 8. August 1883), indem er das Lineal mit der
logarithmischen Theilung in einzelne gleich lange Streifen schneidet, welche in
gleiche Entfernung über einander gesetzt und zu einer „Rechentafel“ vereinigt
werden. Der Schieber wird durch eine gleiche Papiertafel ersetzt, welche aber auf
Glas mit einem stark durchscheinend machenden
Mittel aufgeklebt wird.
Die Herstellung dieser durchscheinenden Maſsstabe und Rechentafeln erfolgt in der
Weise, daſs auf der einen Seite der Glasplatte ein mit Dammarharz bereiteter
Terpentinölfirniſs dünn aufgetragen wird. Das bedruckte Papier wird auf diese Seite
aufgelegt und die Oberfläche mit Spirituslack überzogen:, letzterer durchdringt das
Papier und verwandelt den Dammarfirniſs in ein festes Bindemittel, welches
gleichzeitig dem Papiere die Durchsichtigkeit verleiht.
Die Ausführung der Rechnungen mit Hilfe dieser Rechentafeln ist wie beim
vorhergehenden Apparate. Der durchsichtig gemachte Schieber wird parallel mit sich
selbst auf der darunter liegenden Tafel verschoben.
Einen ganz hübschen Kunstgriff gebraucht Moriz Schinzel in
Groſs-Lobming, Steiermark (* D. R. P.
Nr. 26842 vom 15. Juli 1883) bei seinem
logarithmischen Cubicirungsmaſsstabe. Um die
Inhaltsbestimmung eines Prisma aus den drei Hauptausdehnungen a, b und c durchzuführen,
ist die Summe der drei Logarithmen von a, b und c zu ermitteln.
Schinzel versieht nun, wie aus Textfig. 5 zu entnehmen, den einen Schieber A von dem Nullpunkte aus mit logarithmischer Theilung
sowohl nach links, als nach rechts; das andere Lineal B
ist von einem Endpunkte O
aus getheilt. Stellt man nun den Theilstrich für b
demjenigen für a gegenüber, so kann man dem
Theilstriche von c gegenüber das Product abc ablesen. Der Beweis ist ohne weiteres aus der Figur
zu ersehen. Die Benennungen der Theilungen sind zudem in den üblichen Gröſsen
angegeben, so die Breite und Dicke in Centimeter, die Länge in Meter; der Rauminhalt
kann dann unmittelbar in Cubikmeter abgelesen werden.
Fig. 5., Bd. 260, S. 171 Der zusammenklappbar gemachte Maſsstab ist auſserdem so construirt, daſs
er für gewöhnlich auch zu Längenmessungen dienen kann; es trägt die Rückseite
gewöhnliche Längentheilung, während die logarithmischen Theilungen sich auf der
Vorderseite befinden. Zur Ausführung der Rechnungen wird der Stab in der Mitte
zerlegt und die beiden Hälften dienen als Rechenschieber. Die einen Kanten der
Vorderseite tragen die logarithmische Theilung zur Bestimmung des Inhaltes
prismatischer Körper; an den anderen Kanten sind dagegen zwei Theilungen ebenfalls
nach den oben entwickelten Grundsätzen angebracht, welche die Inhaltsbestimmung für
cylindrische oder kegelförmige Körper von kreisförmigem Querschnitte
ermöglichen.
Zum Theilen von Linien und zum Logarithmenrechnen ist
von Franz
Merl in Speyer (* D. R. P. Nr. 28793 vom 8. April 1884) ein Apparat angegeben, welcher in
Fig. 7
Taf. 11 wiedergegeben ist und in der äuſseren Gestalt einer Schmiege entspricht. Die
Einrichtung wird aus der nachfolgenden Gebrauchsanweisung ohne weiteres klar
werden.
Um eine Linie nach irgend welchem Verhältnisse zu theilen, z.B. in 3 Theile, welche
sich verhalten wie x : y : z, legt man den Apparat so, daſs das Lineal CB mit demjenigen Theilpunkte, welcher der Summe x
+ y + z entspricht, an dem einen Endpunkte B der Linie A B anliegt,
worauf man den Schenkel CA so dreht, daſs dessen innere
Kante durch den Punkte hindurchgeht. Das Lineal FG ist
dabei so gestellt, daſs eine Marke des Schenkels CB bei
F mit dem Nullpunkte der Theilung zusammenfällt.
Verschiebt man nun das mittels Klemmschraube E starr
gemachte System ACB so an der Theilung des Lineals FG von links nach rechts, daſs die erwähnte Marke
zunächst auf den Theilstrich gleich der Entfernung x
und dann auf den gleich der Entfernung x + y zeigt, und zieht nach jeder Verschiebung am Lineal
CA
einen Strich durch AB, so sind natürlich die Durchschnittspunkte die
gewünschten Theilpunkte.
Eine weitere Ergänzung des Apparates bildet eine graphische
Logarithmentafel (Fig. 8 Taf. 11), welche an
dem oberen beweglichen Schenkel befestigt werden kann. Dieselbe ist in der Weise
construirt, daſs man als Fahrstrahlen die Logarithmen, als zugehörige Winkel die
Mantisse der Logarithmen aufgetragen hat. Während mit dem oberen Schenkel CA der Kreisausschnitt ACB
bewegt wird, bleibt der untere Schenkel CB in seiner
Lage und bildet den Fahrstrahl, der mit seiner Länge der Zahl entsprechen muſs; man
sieht z.B. in der gezeichneten Lage, daſs der Logarithmus von 3,15 gleich 0,5 und
der von 10 gleich 1 ist.
(Schluſs folgt.)
Tafeln